Содержание изучаемого материала, методические указания и вопросы для самопроверки, страница 11

Отказы всех элементов схемы – события независимые и представляют собой стационарные пуассоновские потоки с плотностями:

λ_Г1 = 0,08; λ_Г2 = 0,1; λ_Г3 = 0,12; λ_Л1 = 0,2; λ_Л2 = 0,3; λ_Т1 = 0,02; λ_Т2 = 0,04, измеряемых в единицах 1/год.

Определить вероятность бесперебойного питания электроприемников завода в течение времени τ.

Значение τ приведено в табл. 5.

Задача 6. После изготовления универсальный прибор типа «ампер-вольтметр» подвергается проверке на точность измерения тока и напряжения. Прибор считается годным, если ошибка измерения тока не выходит за пределы

± 3 А, а ошибка измерения напряжения – за пределы ± 2 В. Приборы, не удовлетворяющие этим требованиям, возвращаются на доработку. Ошибка измерения тока подчиняется нормальному закону с параметрами m_I и σ_I, а ошибка измерения напряжения – закону равномерной плотности с параметрами m_U и σ_U. Ошибки измерения по току и напряжению – величины независимые.

Значения параметров m_I и σ_I, m_U и σ_U приведены в табл. 6.

Требуется определить, сколько нужно проверить приборов, чтобы с вероятностью не менее 0,9 среди них был хотя бы один годный.

Задача 7. Суммарный ток электрической цепи является линейной функцией четырех случайных аргументов I = I₁ + I₂ + I₃ + I₄. Все четыре тока – непрерывные случайные величины, распределенные по нормальному закону, с параметрами m₁, σ₁; m₂, σ₂; m₃, σ₃; m₄, σ₄, значения которых приведены в табл. 7.

Зависимость между токами задана нормированной корреляционной матрицей:

.

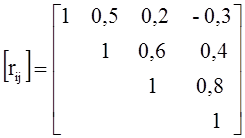Определить значение суммарного тока, которое будет превышено с вероятностью 0,1.

Задача 8. Тепловая мощность, выделяемая в электрической цепи, определяется выражением P = I²R, где ток I и сопротивление R цепи являются независимыми непрерывными случайными величинами. Ток I подчиняется закону равномерной плотности в диапазоне (I₁, I₂), а сопротивление R – нормальному закону с параметрами m_R и σ_R.

Значения I₁, I₂, m_R и σ_R приведены в табл. 8.

Определить математическое ожидание m_Р, дисперсию D_P и среднее квадратическое отклонение σ_Р функции двух случайных аргументов P = P(I, R). Задачу решить двумя методами:

1)  точным; 2) приближенным – методом линеаризации функций случайных аргументов.

Задача 9. От шин понизительной подстанции получает питание потребитель, полная мощность которого определяется нелинейной зависимостью

, где P и Q – активная и реактивная мощности соответственно – являются непрерывными зависимыми случайными величинами, подчиненными нормальному закону с параметрами: m_P, σ_P и m_Q, σ_Q. Коэффициент корреляции между активной и реактивной мощностями r_PQ = 0,4.

Значения параметров m_P, σ_P, m_Q, σ_Q приведены в табл. 9.

Требуется:

1) пользуясь методом линеаризации функций случайных аргументов, определить математическое ожидание m_S, дисперсию D_S и среднее квадратическое отклонение σ_S полной мощности потребителя S;

2) считая, что полная мощность потребителя S также подчинена нормальному закону, как и аргументы P и Q, определить такое ее значение, которое может быть превышено с вероятностью 0,0062.

Задача 10. В результате экспериментальных исследований случайной величины V – отклонений напряжения в электрической сети от номинального значения – зарегистрировано 1000 точек (значений случайной величины V). В табл. 10 приведены интервалы (разряды) отклонений напряжения V и количество точек, попавших в эти интервалы.

Требуется:

1) построить статистический ряд и гистограмму отклонений напряжения V;

2) определить математическое ожидание m_υ, дисперсию D_υ, среднее квадратическое отклонение σ_υ, асимметрию S_k и эксцесс Е_х статистического распределения случайной величины V;

3) используя критерий согласия Пирсона, проверить правдоподобность гипотезы о том, что распределение случайной величины V подчинено нормальному закону;

4) прокомментировать соответствие результата, полученного по критерию согласия Пирсона, значениям асимметрии S_k и эксцесса Е_х и связать это со степенью близости гистограммы и плотности теоретического распределения случайной величины V, график которой необходимо построить на тех же осях, что и гистограмма.