Электротехника \ Основы теории кодирования

Циклические коды. Разработка функциональной схемы кодирующего устройства. Оценка вероятности ошибочного приема символа алфавита, страница 9

x=a

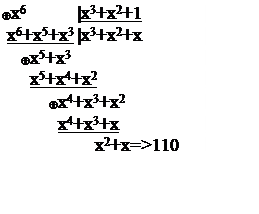
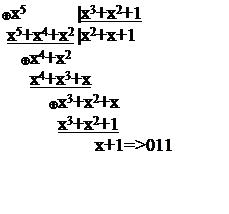
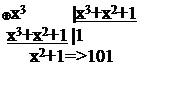
Надпись: Åx6 |x3+x2+1 x6+x5+x3 |x3+x2+x Åx5+x3 x5+x4+x2 Åx4+x3+x2 x4+x3+x x2+x=>110 Надпись: Åx5 |x3+x2+1 x5+x4+x2 |x2+x+1 Åx4+x2 x4+x3+x Åx3+x2+x x3+x2+1 x+1=>011 Надпись: Åx3 |x3+x2+1 x3+x2+1 |1 x2+1=>101

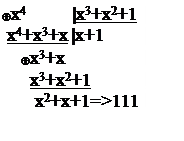
Надпись: Åx4 |x3+x2+1 x4+x3+x |x+1 Åx3+x x3+x2+1 x2+x+1=>111

Сведем полученные результаты в таблицу:

№ вектора

В виде степени xi

В виде двоич. вектора

(старшие разряды слева)

В виде многочлена

1.   

x-¥=0

000

0

2.   

x0=1

001

1

3.   

x

010

x

4.   

x2

100

x2

5.   

x3

101

x2+1

6.   

x4

111

x2+x+1

7.   

x5

011

x+1

8.   

x6

110

x2+x

Часто в таких таблицах есть и логарифмическое представление, которое позволяет производить операции в полях Галуа (умножение, нахождение обратного элемента, нахождение квадратного корня).

Из темы «Арифметика в полях Галуа» известно, что ненулевые элементы поля образуют циклическию группу с размерностью 2m=r=3-1=7, которая порождена примитивным элементом a.

В итоге получим проверочную матрицу, каждый столбец которой представляет синдром ошибки в соответствующем разряде .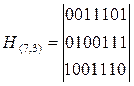

Примечание. Сравнив две матрицы, видим, что мало столбцов совпадает, хотя в литературе часто проверочная матрица строится по проверочному полиному – это ошибочно, так как способ получения проверочной матрицы через проверочный полином не является универсальным. В большинстве случаев, проверочную матрицу нужно строить через примитивные элементы a. Способ построения через проверочный полином пригоден только для полностью цикличных кодов, которые редки.

Надпись: Å0111111 |1101 1101 |0101-это всего лишь результат деления, а не инф-ый вектор, Å001011 так как мы получили ненулевой остаток, что говорит о 1101 наличии ошибок. 110-данный синдром соответствует 7му столбику проверочной матрицы, значит ошибка в седьмом разряде, инвертируем его и получаем 1111111, то есть получили переданную кодовую комбинацию.  Рассмотрим на примере исправление ошибок по синдрому:

Передавалась 12КК C(x)=1111111, под действием помех произошла ошибка в 7-ом разряде, то есть принята C*(x)=0111111 тогда:

После исправления ошибки можно дешифровать исправленную КК разделив ее на образующий полином:

Надпись: Å1111111 |1101 1101 |1011-информационный вектор, соответствующий 12-ой КК Å001011 1101 Å01101 1101 000-нулевой остаток характерен для правильной (трансформированной) КК. Такой способ декодирования довольно сложно реализовать аппаратно, поэтому используют несколько другой алгоритм:

1)  Нахождение остатка от деления C*(x)/g(x)=синдром

2)  Определение веса W остатка – число единиц в остатке

3)  Анализ остатка а) Если W£tи, то C*(x)Åостаток=C(x) исправленная (трансформированная) КК.

б) Если W>tи, то производится циклический сдвиг влево принятой КК на один разряд. И снова осуществляют деление на образующий полином, и снова анализируют вес остатка. Если W>tи, тогда осуществляют еще один циклический сдвиг влево на один разряд принятой КК. Сдвиг влево последовательно на один разряд принятой КК осуществляют до тех пор, пока вес остатка не окажется W£tи. После этого полученную на последнем сдвиге влево КК суммируют по mod 2 с остатком. Для получения исправленной КК результат суммирования с остатком сдвигают циклическим вправо на столько же разрядов, на сколько было сдвинуто влево.

Примечание. Если после произведенных n сдвигов влево остаток от деления W>tи, то в этом случае означает, что процесс декодирования заканчивается только обнаружением ошибки, которую код исправить не в состояни. Таким образом декодер может работать в двух режимах:

- режим обнаружения ошибок (полученно значение синдрома¹0 позволяет игнорировать (не использовать) КК, либо дать сигнал передатчику (нужен обратный канал связи) на повторную передачу, но это усложнит конструкцию и приемника, и передатчика)

- режим обнаружения ошибок с исправлением, при котором синдром используется для поиска места ошибки и ее дальнейшего исправления.

Рассмотрим пример декодирования с исправлением ошибок:

Передаем 12КК C(x)=1111111, под действием помех произошла ошибка в 1-ом разряде, то есть принята C*(x)=1111110 тогда:

Надпись: Å1111110 |1101 1101 |1001-это всего лишь результат деления, а не инф-ый вектор, Å001011 так как мы получили ненулевой остаток, что говорит о 1101 наличии ошибок. Å01100 1101 001-получили ненулевой остаток, что говорит о наличии ошибки. Анализируем вес W<tи=1:

Скачать файл