б) Умножение информационного вектора непосредственно на образующую матрицу C(x)=|a(x)|*|G(n,k)|. Умножение производится по правилам умножения матриц, то есть строка умножается на столбец, сложение по mod 2.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вновь мы получили шестнадцать КК, которые также отвечают параметрам (7,4,3).
Итак, мы построили
циклический код (7,4,3), заданный полиномом g(x)=x3+x2+1, с шестнадцатью КК. Данный код при
пороговом декодировании в состоянии исправить одну ошибку ![]() .
.
Каждый из способов построения имеет свои преимущества и недостатки. Наиболее наглядным является построение умножением информационного вектора на генераторный полином, недостатком такого способа является необходимость умножения, приведения подобных и группировка, что при больших значения n и k, станет довольно затруднительным. При втором способе построения, при комбинировании строк матрицы, появляются одинаковые КК, что приводит к постоянному сравнению вновь полученных КК с предыдущими, а значит и к более сложной программной и аппаратной реализации. Третий способ является довольно наглядным, его возможно реализовать программно, представив матрицу в виде двухмерного массива двоичных символов.
Исходя из параметров кода (7,4,3), генераторного полинома g(x)=x3+x2+1 и построенных кодовых комбинаций, разработаем схему кодирующего устройства. Так как параллельный код создает определенные трудности при передаче в линию связи, то в нашем случае кодирующее устройство будет формировать последовательный код. Для формирования циклических кодов используются переключающие схемы. Кодирующее устройство в общем случае выполняет операцию умножения информационного вектора на генераторный полином, то есть C(x)=a(x)*g(x). Рассмотрим общую схему кодирующего устройства:
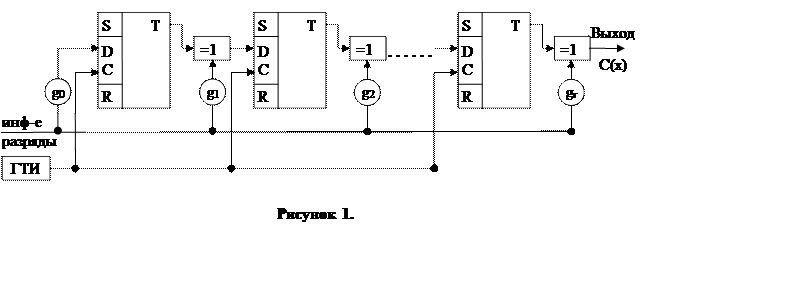
Общая структура построения схем умножения состоит в том, что каждая сборка содержит ячейку памяти (D-триггер) и сумматор по mod 2. Таким образом для реализации кодирующего устройства последовательного кода необходимо иметь r-ячеек памяти и r-сумматоров по mod 2.
Коэффициенты gi определяются по генераторному полиномому и принимают значение 0 или 1.
Если gi=1 – существует обратная связь,
gi=0 – разрыв цепи.
В нашем случае необходимо осуществить умножение информационного вектора a(x)=a0+a1x+a2x2+a3x3 на генераторный полином g(x)=x3+x2+1.
Для построения структурной схемы умножения необходимо иметь три ячейки памяти (r=n-k=7-4=3) и два сумматора по mod 2.
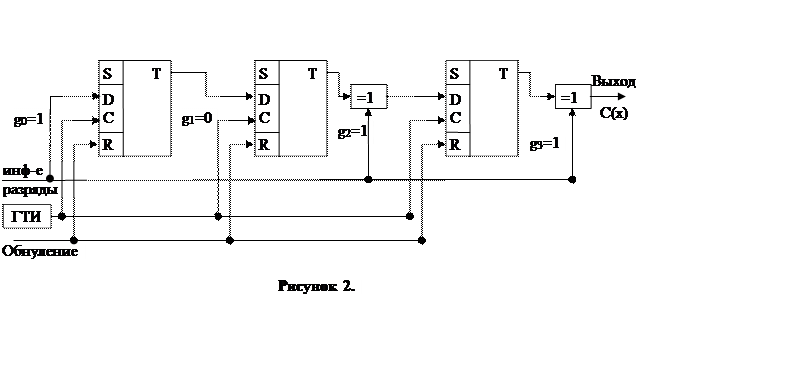
Основываясь на разработанной структурной схеме кодирующего устройства, разработаем функциональную схему кодирующего устройства (рис. 3), которое будет построено на интегральных микросхемах серии 564 (стандартная логика):
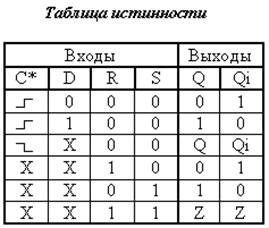
1) К564ТМ2 (аналоги в сериях К561 и К576) – два В-триггера с динамическим управлением.
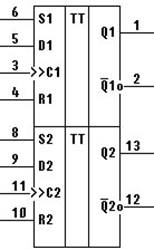
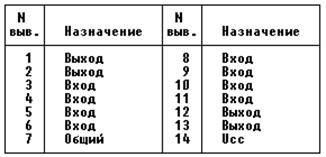
2) К564ЛП2 (аналоги в сериях К561 и К576) – четыре логических элемента исключающее ИЛИ (сумматор по mod 2).
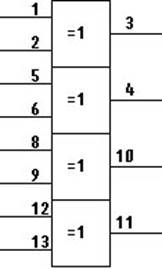
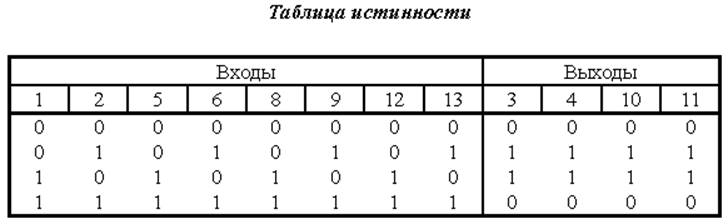
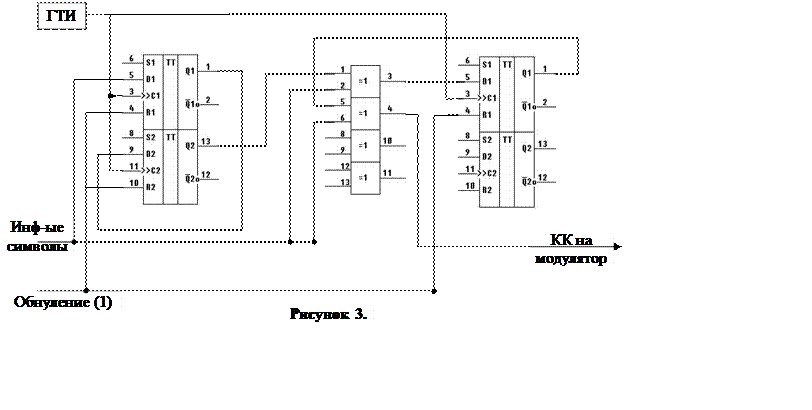
Особенности работы кодера.
1) Перед работой схемы необходимо осуществить обнуление триггеров по входу R (4), для этого необходимо подать логическую единицу.
2) Информационный вектор подается старшими разрядами вперед.
3) После окончания информационно вектора (k=4) необходимо подать три нуля (n-k=7-4=3).
4) Последний бит КК будет постоянно подаваться в канал связи, для того, что бы этого избежать необходимо установить двухвходовой конъюнктор (2И) и соединить его с ГТИ и выходом кодера.
5) Синхронная работа кодера обеспечивается подачей логической единицы (с ГТИ) на вход триггеров C (3), которые срабатывают по фронту тактового импульса.
Принцип работы кодера.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.