Циклические коды. Разработка функциональной схемы кодирующего устройства. Оценка вероятности ошибочного приема символа алфавита, страница 8

2)  Декодирование по максимуму правдоподобия, такое декодирование позволяет использовать потенциальные возможности кода по коррекции ошибок, то есть .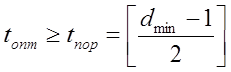

Рассмотрим оба способа декодирования, хотя следует заметить, что декодирование по максимуму правдоподобия более характерно для кодов БЧХ, у которых =>.

Алгоритм порогового декодирования.

Задача при исправлении ошибок состоит в том, что бы определить:

1)  место ошибки (разряд);

2)  исправить ошибку.

Пороговое декодирование по синдрому использует операцию деления:

C*(x)/g(x)

1)  если синдром (остаток) равен нулю, то ошибки нет, то есть КК принята правильно, либо трансформирована, такую комбинацию можно дешифровать

2)  если синдром (остаток) не равен нулю, то в КК есть ошибки.

Для реализации используется проверочная матрица полиномиального кода. В теории кодирования проверочная матрица представляется двумя способами:

1)  через проверочный полином;

2)  через примитивные элементы a.

Определим проверочную матрицу через проверочный полином:

.

Этот способ определения проверочного полинома хорошо работает для полностью циклических кодов, которые встречаются редко.

Проверочная матрица по проверочному полиному будет выглядеть, как:

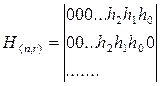, где  - коэффициенты проверочного полинома.

Коэффициенты записываются справа на лево, последующие строки получаются циклическим сдвигом влево. До n-го столбца происходит дополнение нулями.

Построим проверочную матрицу данным способом для нашего кода:

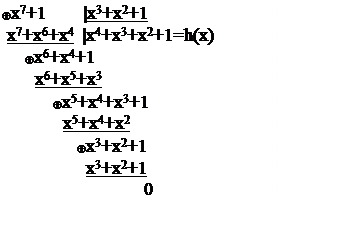
Частное от деления и есть проверочный полином, построим по нему проверочную матрицу:

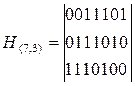
Так как проверочная матрица (многочлен) образована разультатом деления на образующий полином, то каждый столбец представляет собой остаток от деления принятой КК (козможно с ошибками) на образующий полином. Указанный остаток от деления называют синдромом ошибки или определителем места ошибки в КК.

Если принятая кодовая комбинация без ошибок, то результат деления (остаток) на образующий полином будет равен нулю, поэтому столбца, состоящего из одних нулей в проверочной матрице нет.

Примечание. Нулевой остаток от деления может быть получен и при условии перерождения (трансформации) одной разрешенной КК в другую разрешенную КК под действием помех в канале связи. Очевидно, что при трансформации декодер не в состоянии ни исправить, ни обнаружить ошибку, поэтому это одно из наиболее опасных явлений.

Таким образом, для каждой ошибки существует свой синдром, двоичная запись синдрома представляет собой столбец проверочной матрицы. Данным спсобом построения проверочной нужно пользоваться с осторожностью, потому что он работает не для всех кодов.

Определим проверочную матрицу через примитивные элементы a.

Данный способ построения проверочной матрицы является универсальным представлением проверочной матрицы, которую на практике используют для коррекции ошибок. Представим проверочную матрицу через примитивые элементы a (вычеты) по модулю образующего полинома. Таким образом, для постороения проверочной матрицы способом определения вычетов в поле Галуа GF(2^r)= GF(2³)= GF(8) необходимо найти вычеты по mod g(x):.

0(mod g(x)=x³+x²+1)=0=> двоичное представеление будет 000, этот вычет соответствует отсутствию ошибок или трансформации, поэтому в конечном итоге данный вычет в проверочной матрице отсутствует.

1(mod g(x)=x³+x²+1)=1=> двоичное представеление будет 001, которое и будет первым столбцом проверочной матрицы и соответствует ошибке в первом разряде.

a(mod g(x)=x³+x²+1)= a=>010-второй столбец матрицы.

a²mod g(x)=x³+x²+1)= a²=>100-третий столбец матрицы.

Далее идет элемент a³, который имеет порядок m=3, но из темы «Арифметика в полях Галуа» известно, что в составе элементов поля должны быть элементы со степенью m=r<3, так как векторное представление элементов поля в двоичной форме должно иметь m=r=3 разряда, поэтому