
















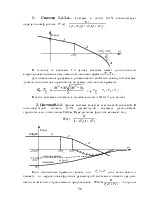


Динамический синтез с использованием запретных зон
Определение параметров среднечастотной зоны желаемой ЛАХ
Параметры желаемой ЛАХ в этой области определяются требуемым качеством переходного процесса. В методе Бесекерского (метод динамического синтеза) за основной показатель принимается М - показатель колебательности.
 По передаточной функции замкнутой системы
По передаточной функции замкнутой системы ![]() получают
ее частотную характеристику
получают
ее частотную характеристику ![]() , а по ней -
амплитудно-частотную:
, а по ней -
амплитудно-частотную: ![]() .
.
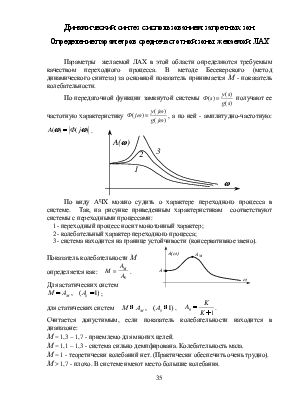
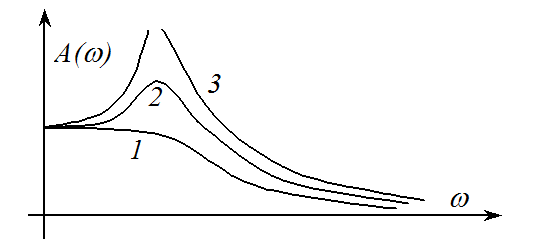
По виду АЧХ можно судить о характере переходного процесса в системе. Так, на рисунке приведенным характеристикам соответствуют системы с переходными процессами:
1- переходный процесс носит монотонный характер;
2- колебательный характер переходного процесса;
3- 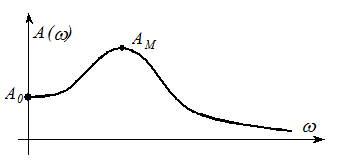 система находится на границе устойчивости (консервативное
звено).
система находится на границе устойчивости (консервативное
звено).
Показатель колебательности М определяется как: 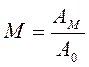 .
.
Для астатических систем
![]() ;
;
для статических систем ![]() ,
, ![]() .
.
Считается допустимым, если показатель колебательности находится в диапазоне:
М = 1,3 – 1,7 - приемлемо для многих целей.
М = 1,1 – 1,3 - система сильно демпфирована. Колебательность мала.
М = 1 - теоретически колебаний нет. (Практически обеспечить очень трудно).
М > 1,7 - плохо. В системе имеют место большие колебания.
Связь между показателем колебательности М
и характеристиками переходного процесса
Установим ее из предположения, что основная часть переходного процесса определяется доминирующими корнями. Нас интересует колебательный процесс. Такой процесс определяется двумя доминирующими комплексными корнями. Другими словами, поведение системы сводим к поведению колебательного звена:
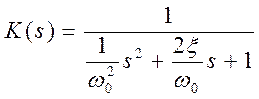
Здесь x - коэффициент демпфирования (затухания).
w0 - частота собственных, недемпфированных колебаний.
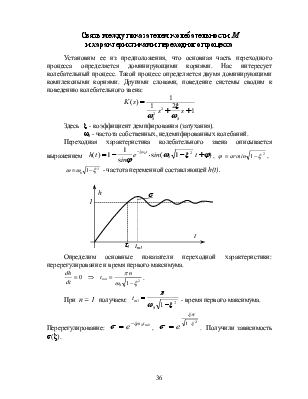
Переходная
характеристика колебательного звена описывается выражением 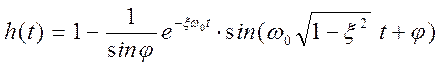 ,
, ![]() ,
,
![]() - частота переменной
составляющей h(t).
- частота переменной
составляющей h(t).
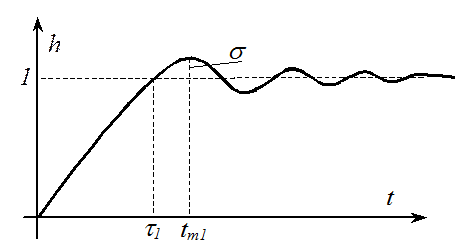
Определим основные показатели переходной характеристики: перерегулирование и время первого максимума.
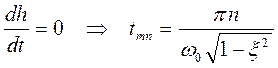 .
.
При n
= 1 получаем: 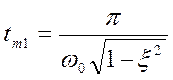 - время
первого максимума.
- время
первого максимума.
Перерегулирование: ![]() ,
, 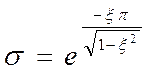 .
Получили зависимость s(x).
.
Получили зависимость s(x).
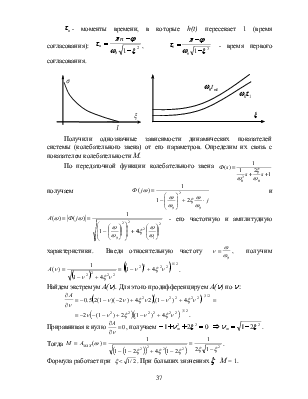
![]() - моменты времени, в которые h(t)
пересекает 1 (время согласования):
- моменты времени, в которые h(t)
пересекает 1 (время согласования): 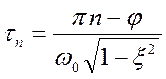 ,
,
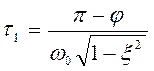 - время первого согласования.
- время первого согласования.
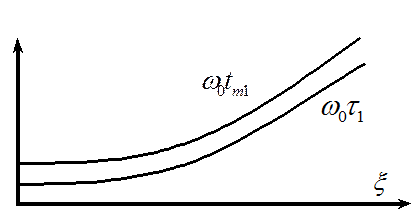
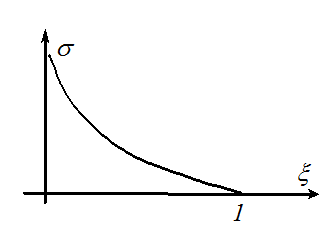
Получили однозначные зависимости динамических показателей системы (колебательного звена) от его параметров. Определим их связь с показателем колебательности М.
По
передаточной функции колебательного звена 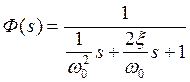 получаем
получаем 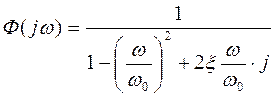 и
и 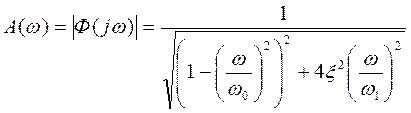 -
его частотную и амплитудную характеристики. Введя относительную частоту
-
его частотную и амплитудную характеристики. Введя относительную частоту 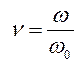 ,
получим
,
получим 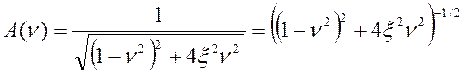 .
.
Найдем экстремум А(n). Для этого продифференцируем А(n) по n:
![]()
![]() .
.
Приравнивая к нулю ![]() , получаем
, получаем ![]() .
.
Тогда
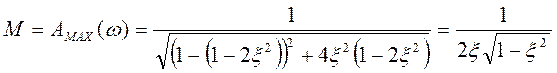 .
.
Формула работает при ![]() . При больших значениях x М
= 1.
. При больших значениях x М
= 1.
Получили зависимость М(x). Выше получили s(x). Следовательно, можно определить взаимосвязь М(s) и, соответственно, s(М).
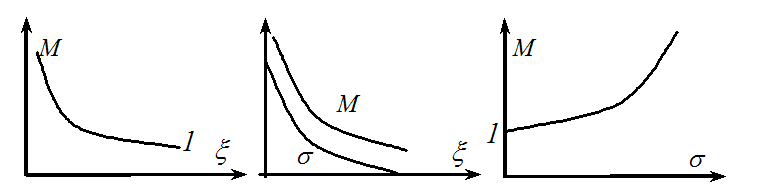
Аналогично получаются
зависимости ![]() и
и ![]() .
.
Отсюда, показатель колебательности М однозначно определяет такие важные динамические характеристики системы, как перерегулирование, время первого согласования, первого максимума и, как показывают расчеты, время переходного процесса. Следовательно, М - обобщенная динамическая характеристика системы (звена второго порядка).
Запретная зона на плоскости АФЧХ разомкнутой системы
 При рассмотрении частотного критерия Найквиста было отмечено:
При рассмотрении частотного критерия Найквиста было отмечено:
Если годограф разомкнутой системы не входит в определенную окрестность точки (-1, j0), то в системе обеспечивается некоторый запас устойчивости; следовательно, речь может идти о качестве переходного процесса.
Построим эту область с учетом показателя колебательности М.
Частотные характеристики замкнутой системы однозначно определяются частотной характеристикой разомкнутой системы, ее вещественной и мнимой частями:
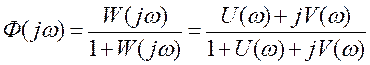 ,
, 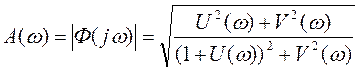 .
.
Построим линии равного уровня амплитудной
характеристики замкнутой системы на плоскости АФЧХ разомкнутой системы. Для
этого обозначим ![]() , что действительно
имеет место при
, что действительно
имеет место при ![]() .
.
Тогда 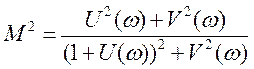 .
Выполняя преобразования, последовательно получаем:
.
Выполняя преобразования, последовательно получаем:
![]() ,
,
![]() ,
,
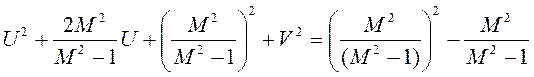 .
.
Последнее
выражение есть уравнение окружности ![]() , где
, где 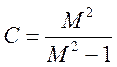 -
центр этой окружности, а
-
центр этой окружности, а ![]() - ее радиус.
- ее радиус.
Получили, что
размеры и положение этой окружности определяются параметром М. Следовательно, если потребовать
выполнения условия ![]() , то построенная
окружность приобретает свойства запретной зоны, куда не должна заходить АФЧХ
разомкнутой системы. Другими словами, это и есть запретная зона. Уравнение
запретной зоны получено в декартовой системе координат.
, то построенная
окружность приобретает свойства запретной зоны, куда не должна заходить АФЧХ
разомкнутой системы. Другими словами, это и есть запретная зона. Уравнение
запретной зоны получено в декартовой системе координат.
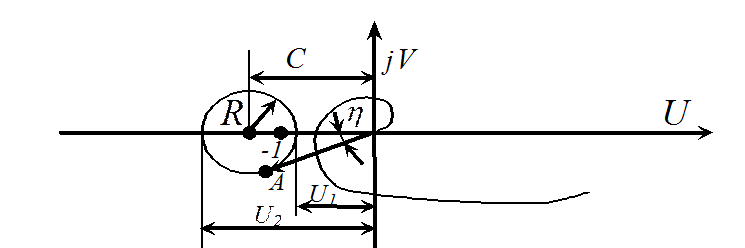
При уменьшении М запретная зона увеличивается (радиус R растет) и, наоборот, при увеличении М размеры запретной зоны уменьшаются.
Получим уравнение запретной зоны в полярных координатах. Определим границы запретной зоны (расстояние от оси ординат):
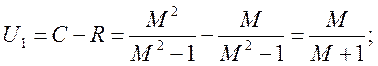
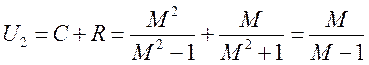 .
.
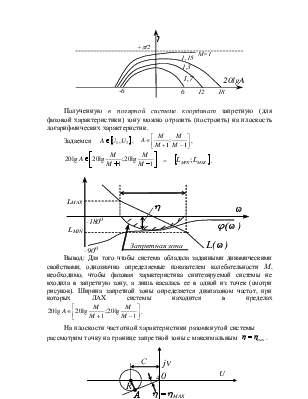
Построим вектор, соединяющий начало координат «0» с любой точкой этой окружности (он определяется длиной вектора А и углом η).
![]() .
.
Угол η определяет запас устойчивости по фазе, соответствующий определенной точке окружности. Из курса тригонометрии имеем:
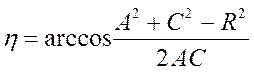 .
.
Для получения
запретной зоны следует построить кривую ![]() .
Задавшись М=const и изменяя A
= var
.
Задавшись М=const и изменяя A
= var ![]() , можно получить зависимости
, можно получить зависимости ![]() (семейство запретных зон) или
(семейство запретных зон) или ![]() для различных М.
для различных М.

Полученную в полярной системе координат запретную (для фазовой характеристики) зону можно отразить (построить) на плоскость логарифмических характеристик.
Задаемся ![]() ,
,
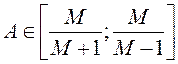 ,
,
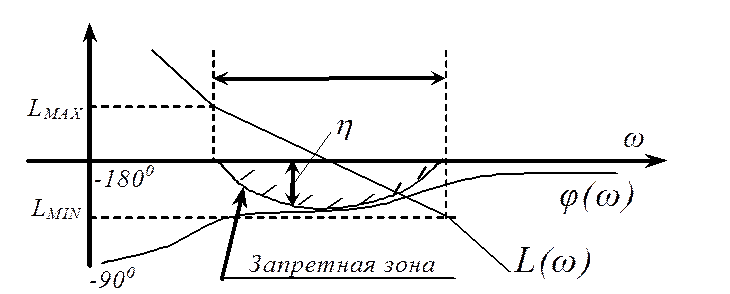
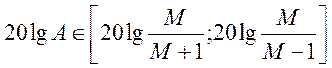 =
= ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.