Динамический синтез с использованием запретных зон. Определение параметров среднечастотной зоны желаемой ЛАХ, страница 4

Для всех М из диапазона:   1.1≤ М≤1.8  это допущение  справедливо.

То есть система 1-2-1-2 в области средних частот эквивалентна системе 2-1-2, значит можно применять формулы:

         

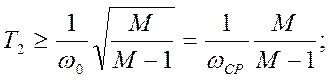
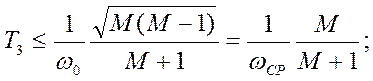
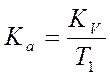    в данном случае  ,   то есть  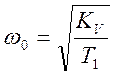и, кроме того, .

Для Т₃ существует более точная формула:

.

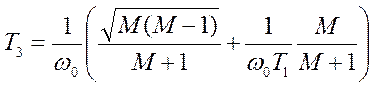Основная погрешность в расчетах параметров систем определяется переходом от точных к приближенным формулам. Но использование для расчетов приближенной характеристики j(w) повышает запас устойчивости исходной системы:

5. Система 1-2-1-2-3-4-... (малые инерционности в системе с астатизмом первого порядка)

Передаточная функция такой системы

.

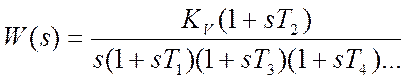Границы запретной зоны, как и в рассмотренных ранее случаях, можно определить из неравенств:

   

   .

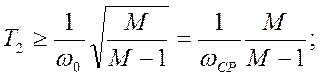
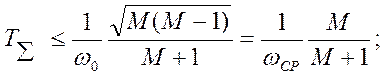
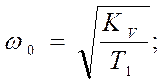
6. Учет нестабильности параметров для системы 1-2-1-2

Нестабильность параметров приводит к отклонению М от расчетного (ожидаемого) значения. 

Переход от системы 1-2-1-2 к системе 2-1-2 при   справедлив  и с точки зрения учета нестабильности параметров.

Тогда 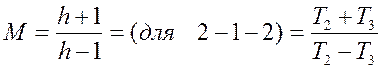.   Отсюда  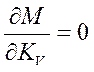 и 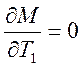,  так как К_V и T₁ влияют на точность, а не на динамику (переходный процесс) системы. На изменение динамических свойств системы влияет нестабильность Т₂ и Т₃. Определив функции чувствительности М по этим постоянным (аналогично системе 2-1-2), получаем отклонение показателя колебательности от расчетного значения: 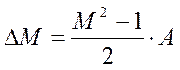,  где для детерминированного ухода параметров , а для случайного: .

Отсюда расчетное значение , (А≠0), используемое для определения Т₂ и Т₃.

7. Учет нестабильности параметров для системы 1-2-1-2-3-4-...

Для данной системы все рассуждения аналогичны предыдущему случаю. Единственным отличием является то, что вместо Т₃ применяется 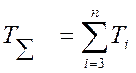. Расчетные формулы остаются неизменными.

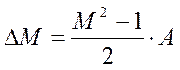;   ,   или ,

.

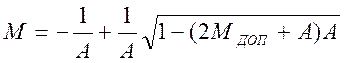Хотя, если быть строгим, то следует получить функции чувствительности М по всем постоянным времени, составляющим 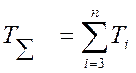, с последующим уточнением .

8. Система 0-1-2-1-2 (Статическая симметричная система) 

Передаточная функция разомкнутой системы и ее частотные характеристики имеют вид:

.

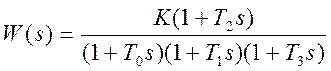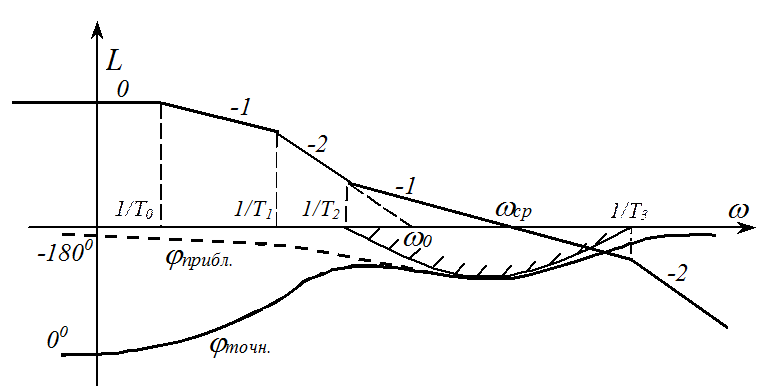
Ситуация значительно упрощается, если     и   , или     и    . Тогда передаточная функция системы (в среднечастотной области) преобразуется к виду 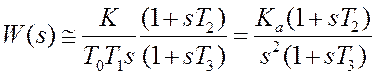 , где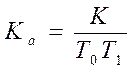. Получили систему вида 2-1-2 (применительно к области средних частот). Далее для реализации требуемого качества переходных процессов определяются постоянные времени:

,  ,   .             

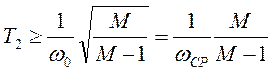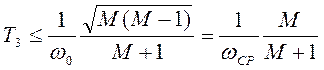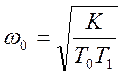Постоянные Т₀ и Т₁  выбираются из условия необходимой точности системы в статическом и динамических режимах, причем Т₁ может быть подвергнута коррекции  в процессе сопряжения низкочастотного и среднечастотного участков ЛАХ.

При необходимости значение Т₃ можно уточнить:

.

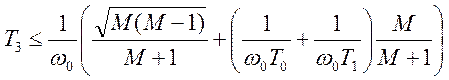9. Система 0-1-2-1-2-3-4... (Статическая симметричная система с малыми инерционностями)

Для данной системы расчет среднечастотной области с целью обеспечения требуемой динамики выполняется по аналогичным формулам:

,  ,   ,              

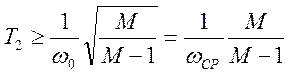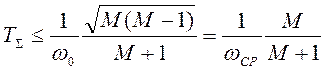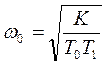или 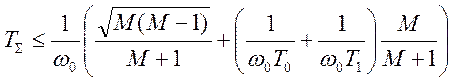, где .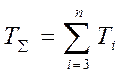

10. Учет нестабильности параметров в статических симметричных системах

Рассматриваются случаи, когда  и   ,  или   и 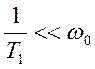 . Показатель колебательности 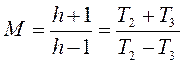 . Функции чувствительности и отклонение М от расчетного (заданного) значения определяются также, как и для случая системы 2-1-2, то есть:

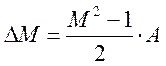,    где   (при детерминированном уходе),

 (при случайном уходе параметров),

  .

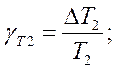
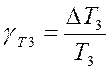Приведенные формулы справедливы для системы 0-1-2-1-2. В случае системы 0-1-2-1-2-3-4...  применяются уточненные формулы:

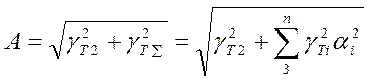   -  случайный уход, или  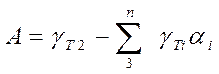   - детерминированный уход параметров.

Расчетное значение М для определения Т₂ и Т₃ имеет в обоих случаях один и тот же вид: 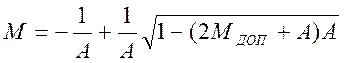         , (А≠0).

11. Статические системы с колебательными звеньями

.

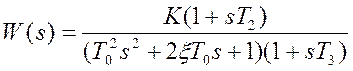Синтез среднечастотной области ЛАХ таких систем осуществляется относительно просто в случаях, когда собственная частота колебательного звена расположена вне рассматриваемой области частот, то есть в низкочастотной или в высокочастотной областях ЛАХ. Если же она принадлежит области средних частот, то учет его очень сложен, и в нашем курсе не исследуется.