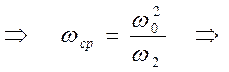
![]() .
.
Тогда
окончательно 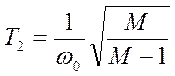 ,
, 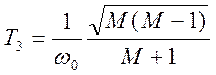 .
.
Обычно система
настраивается таким образом, чтобы ее качество было не хуже заданного.
Применительно к нашему случаю должно выполняться неравенство ![]() . Здесь Мдоп - расчетное значение
показателя колебательности (используемое для определения постоянных Т2 и Т3). С учетом данного требования получаем:
. Здесь Мдоп - расчетное значение
показателя колебательности (используемое для определения постоянных Т2 и Т3). С учетом данного требования получаем:
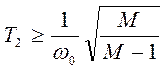 ,
,
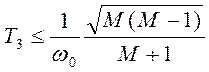 , или
, или 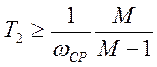 ,
, 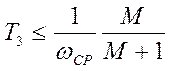 .
.
Дополнительно можно отметить тот факт, что
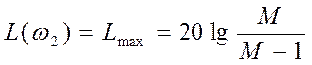 ,
,
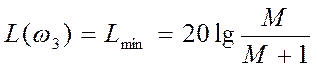 , а w2
и w3 - граничные точки запретной зоны по
фазе (смотри рисунок в начале пункта).
, а w2
и w3 - граничные точки запретной зоны по
фазе (смотри рисунок в начале пункта).
ЛАХ типа 1-2 (с наклонами -1, -2)
Передаточная функция системы
имеет вид: 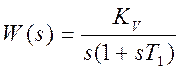 .
.
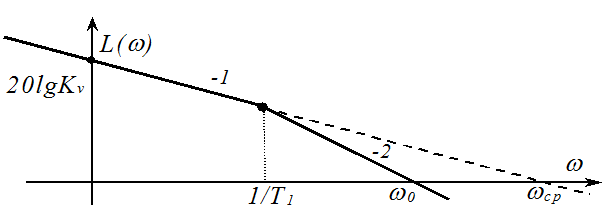
Частота среза wср введена условно.
Частотные
характеристики разомкнутой и замкнутой систем соответственно равны: 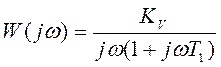 ,
, 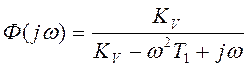 (при
Wос(s)=
1).
(при
Wос(s)=
1).
Показатель
колебательности ![]() , где
, где 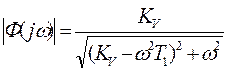
Для
нахождения Ам необходимо
получить уравнение 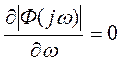 , откуда последовательно
найдем
, откуда последовательно
найдем ![]() :
:
![]() .
.
![]() .
.
![]() ,
,
![]() ,
, 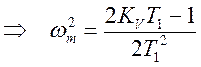 .
.
Подставим ![]() в
в ![]()
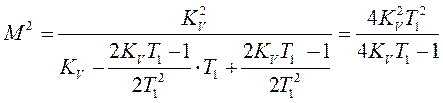 .
.
Окончательно получаем 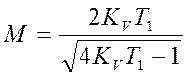 .
.
Если в выражении
для М ввести обозначение ![]() , тогда из уравнения
, тогда из уравнения ![]() после преобразований:
после преобразований: ![]()
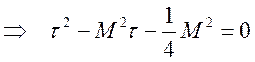 ,
будем иметь
,
будем иметь 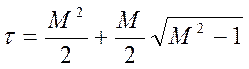 , и искомое
неравенство
, и искомое
неравенство 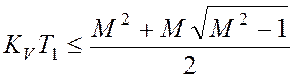 , позволяющее
определить Т1 из условия
требуемого показателя колебательности системы М.
, позволяющее
определить Т1 из условия
требуемого показателя колебательности системы М.
Ниже изображены частотные характеристики разомкнутой системы.
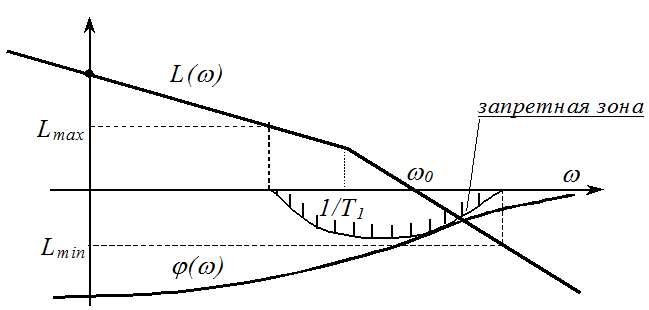
Расчет среднечастотной области ЛАХ системы
на базе типовой ЛАХ 2-1-2
(Предварительно перед изучением каждого пункта
следует повторить материал на стр. 42-45)
1. Система 2-1-2-3-4-5-... (учет малых инерционностей)
Передаточная функция такой системы:
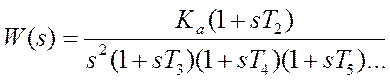 , при этом
, при этом 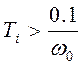 , i = 4, 5, …
, i = 4, 5, …
Частотные
характеристики системы изображены ниже на рисунке. Данная система при
определенном соотношении параметров может быть, в отличие от системы 2-1-2,
неустойчивой. Границы запретной зоны в области средних частот (точки перегиба
ЛАХ) определяются как: 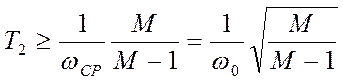 (аналогично
системе 2-1-2);
(аналогично
системе 2-1-2);
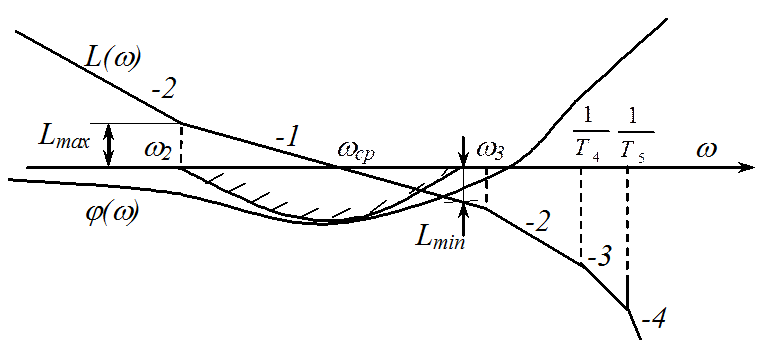
вместо неравенства для
определения постоянной времени Т3
используют неравенство вида 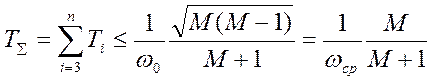 , взаимно
увязывающее постоянные времени Т3,
Т4, Т5, … Как следует из рисунка, ω3 находится правее границы
запретной зоны по фазе. Сдвиг ω3
вправо является компенсационной мерой более интенсивного роста фазовой
характеристики вследствие наличия постоянных Т4,
Т5, …
, взаимно
увязывающее постоянные времени Т3,
Т4, Т5, … Как следует из рисунка, ω3 находится правее границы
запретной зоны по фазе. Сдвиг ω3
вправо является компенсационной мерой более интенсивного роста фазовой
характеристики вследствие наличия постоянных Т4,
Т5, …
Такой подход к определению параметров среднечастотной области не идеален. Погрешность результата в некоторых случаях может достигать до 10%. Но получение симметричной ЛАХ (типа 2-1-2) в области средних частот считается значительным достижением.
2. Учет нестабильности параметров в системе 2-1-2
Показатель
качества системы ![]() (показатель
колебательности).
(показатель
колебательности).
Определим
функции чувствительности 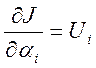 . Ранее
получили
. Ранее
получили 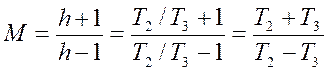 .
.
Тогда 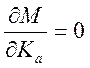 ,
, 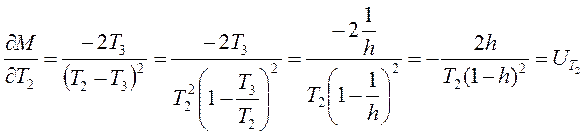 ,
,
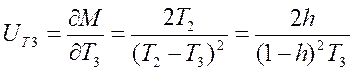 .
.
В результате отклонение показателя колебательности М от расчетного значения при изменении параметров системы будет равно:
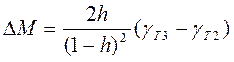 - при детерминированном уходе,
и
- при детерминированном уходе,
и
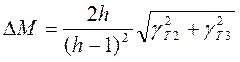 - при случайном уходе, где
- при случайном уходе, где 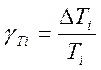 - относительное изменение
(уход) постоянной времени.
- относительное изменение
(уход) постоянной времени.
Упростим полученные выражения.
Нам известно,
что ![]() , тогда
, тогда ![]() .
.
Отсюда 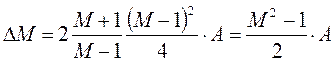 где
где 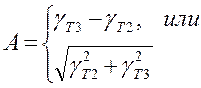
Далее, после
соответствующих преобразований, с учетом ![]() (или граничный случай
(или граничный случай ![]() ):
):
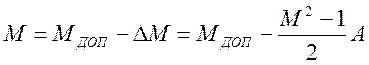 ,
,
![]() ,
,
![]() , получаем:
, получаем: 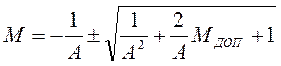 , или (оставляем правильный
знак)
, или (оставляем правильный
знак) 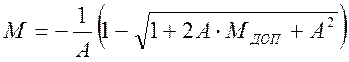 - расчетное значение показателя
колебательности М, используемого
при определении параметров среднечастотной области ЛАХ с учетом их (параметров)
возможной вариации.
- расчетное значение показателя
колебательности М, используемого
при определении параметров среднечастотной области ЛАХ с учетом их (параметров)
возможной вариации.
3. Учет нестабильности параметров в системе 2-1-2-3-4-…
Методика уточнения расчетного показателя колебательности М с учетом возможных отклонений параметров системы аналогична рассмотренному ранее случаю.
Результаты не должны отличаться от полученных в предыдущем пункте, приведенных к выражению
![]() ,
, 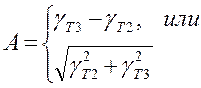 .
.
При этом должен быть учтен важный момент: при совместном изменении постоянных Т3, Т4, Т5, …, их сумма в любом случае должна удовлетворять неравенству:
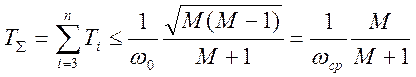 .
.
4. Система 1-2-1-2 (Система с астатизмом первого порядка)
Ее
передаточная функция имеет вид: 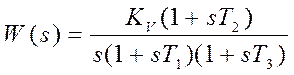 .
.
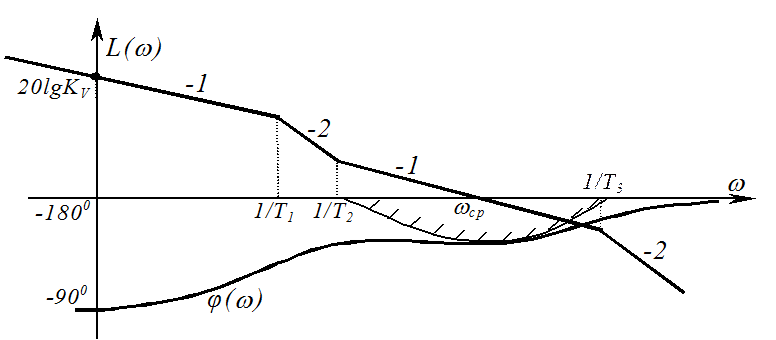
В большинстве
случаев ![]() , и при этом соотношении низкочастотная
зона удалена от среднечастотной области. Следовательно, при частотах средней области,
можно принять:
, и при этом соотношении низкочастотная
зона удалена от среднечастотной области. Следовательно, при частотах средней области,
можно принять:
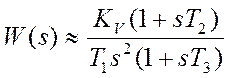 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.