Вывод: Для того чтобы
система обладала заданными динамическими свойствами, однозначно определяемые
показателем колебательности М, необходимо,
чтобы фазовая характеристика синтезируемой системы не входила в запретную зону,
а лишь касалась ее в одной из точек (смотри рисунок). Ширина запретной зоны
определяется диапазоном частот, при которых ЛАХ системы находится в пределах 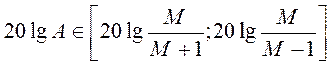 .
.
На плоскости
частотной характеристики разомкнутой системы рассмотрим точку на границе запретной
зоны с максимальным ![]() .
.
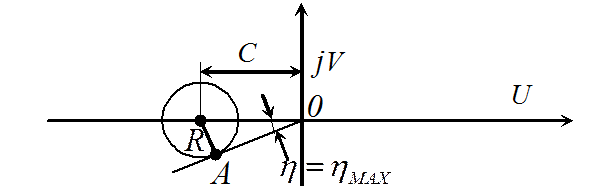
Из теоремы Пифагора следует:
![]() .
.
При
![]()
![]() ,
и
,
и 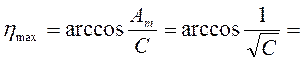
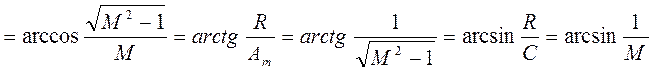 .
.
Типовые ЛАХ, используемые в среднечастотной области
Методика определения параметров разомкнутой системы в среднечастотной области определяется типом (видом) ЛАХ в этом диапазоне частот. Рассмотрим наиболее важные случаи, к которым в дальнейшем будут сведены другие логарифмические характеристики.
ЛАХ типа 2-1 (с наклонами -2, -1)
Передаточная
функция разомкнутой системы, у которой ЛАХ имеет указанные наклоны,
определяется выражением ![]() .
.
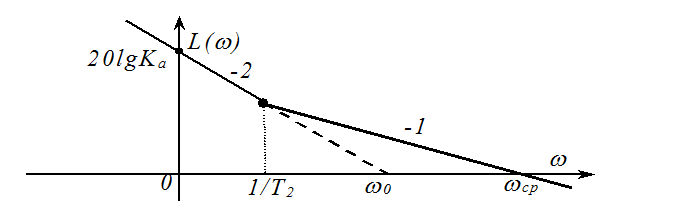
Ка - добротность системы по
ускорению. ![]() (проверяется легко).
(проверяется легко).
Считаем, что добротность по ускорению Ка известна из условия точности, следовательно, запас устойчивости (и требуемые динамические свойства) определяется только постоянной Т2.
Для определения Т2 по передаточной функции
замкнутой системы 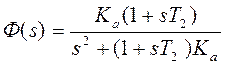 получим частотные
характеристики:
получим частотные
характеристики:
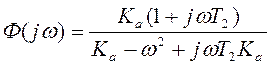 - АФЧХ,
- АФЧХ, 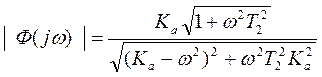 - ВЧХ.
- ВЧХ.
Показатель колебательности ![]() . Для его нахождения
выполняется дифференцирование
. Для его нахождения
выполняется дифференцирование ![]() . Далее,
решая уравнение
. Далее,
решая уравнение ![]() относительно w, находим wm, которая после
подстановки в
относительно w, находим wm, которая после
подстановки в ![]() позволит получить
выражение, связывающее М и Т2 . Схематично данная
последовательность действий изображается в виде:
позволит получить
выражение, связывающее М и Т2 . Схематично данная
последовательность действий изображается в виде: ![]() .
.
В результате получаем неравенство
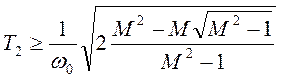 , позволяющее определить точку
излома ЛАХ (частоту излома 1/Т2).
Все промежуточные вычисления ввиду их сложности опущены. Если учесть, что
, позволяющее определить точку
излома ЛАХ (частоту излома 1/Т2).
Все промежуточные вычисления ввиду их сложности опущены. Если учесть, что ![]() , то неравенство, определяющее Т2, преобразуется к виду
, то неравенство, определяющее Т2, преобразуется к виду 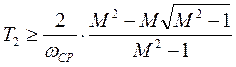 . (Рекомендуется данный переход
выполнить самостоятельно).
. (Рекомендуется данный переход
выполнить самостоятельно).
При определении Т2 обошлись без построения запретной зоны для фазовой характеристики. Но можно с уверенностью сказать, данная характеристика рассматриваемой системы не зайдет в эту зону, однозначно определяемую показателем колебательности М, и, значит, в синтезируемой системе будут реализованы требуемые качества переходного процесса.
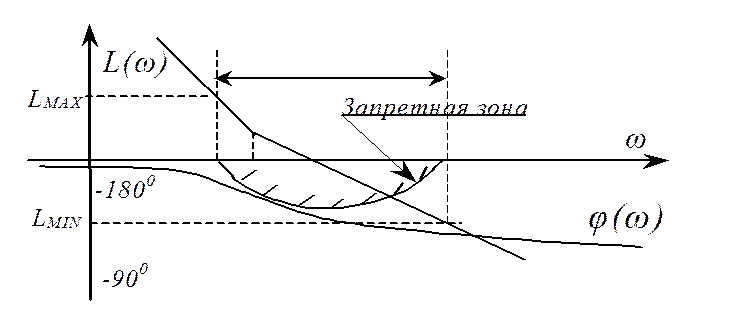
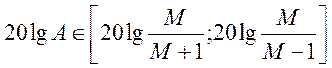 =
= ![]() .
.
Рассмотренный случай системы с типовой ЛАХ типа 2-1 встречается редко. Такие системы применяются в качестве интегрирующих в маломощных приводах.
ЛАХ типа 2-1-2 (с наклонами -2, -1, -2)
Передаточная
функция разомкнутой системы с данной типовой ЛАХ имеет вид: 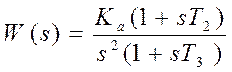 , причем
, причем ![]() .
.
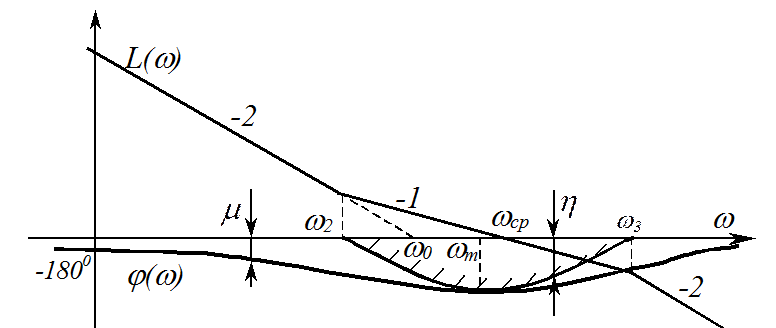
Запас по фазе ![]() .
.
Нам известно, что 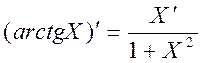 .
.
Тогда для определения максимального запаса по фазе вычислим
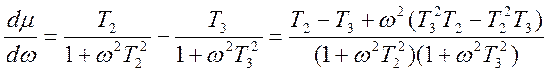 и,
с целью отыскания экстремума, из уравнения
и,
с целью отыскания экстремума, из уравнения ![]() ,
преобразуемого к виду
,
преобразуемого к виду ![]() , получаем
, получаем 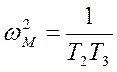 и
и 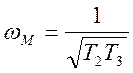 .
.
Далее, после
подстановки значения ![]() в выражение для m, с учетом того, что
в выражение для m, с учетом того, что ![]() , вычислим искомое
, вычислим искомое
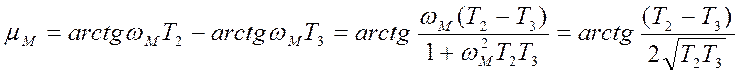 .
.
Введем понятие «протяженность
линии единичного наклона» ![]() .
.
Тогда 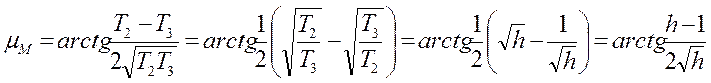 .
.
Необходимый
запас устойчивости системы по фазе ![]() , а значит и
параметры ЛАХ, будем определять из условия, что АФЧХ разомкнутой системы коснется
запретного круга, соответствующего требуемому показателю колебательности М, что соответствует уравнению
, а значит и
параметры ЛАХ, будем определять из условия, что АФЧХ разомкнутой системы коснется
запретного круга, соответствующего требуемому показателю колебательности М, что соответствует уравнению ![]() , где
, где 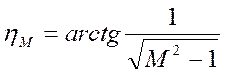 - максимальное значение угла в
запретной зоне по фазе, было определено ранее.
- максимальное значение угла в
запретной зоне по фазе, было определено ранее.
Тогда из уравнения
![]()
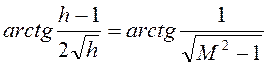 получаем
получаем
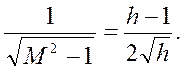 Откуда
Откуда 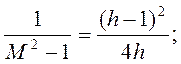
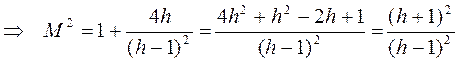 , и окончательно -
, и окончательно - 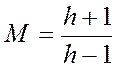 .
.
Вывод: Показатель колебательности М однозначно связан с протяженностью зоны единичного наклона ЛАХ h. Увеличение протяженности зоны единичного наклона ЛАХ ведет к снижению колебательности. И наоборот.
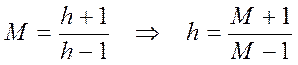 (рекомендуется проверить).
(рекомендуется проверить).
Определим основные параметры этой зоны.
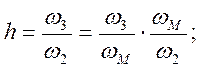
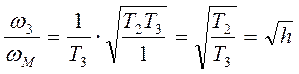 ;
; 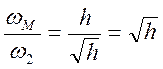 .
.
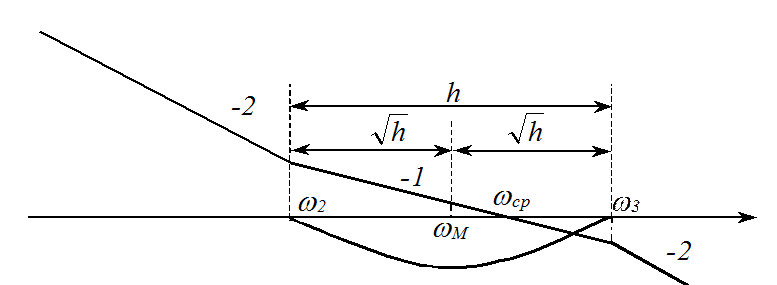
Установим взаимосвязь wср с wм.
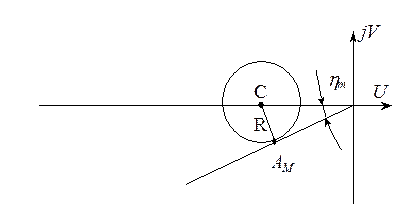
Ранее было получено
![]() .
.
![]() при
при ![]() ,
,
![]() при
при ![]() .
.
Так как наклон L(w) = - 1, то должно выполняться
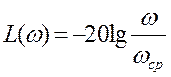 и
и
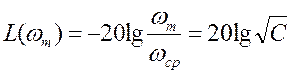 , откуда
, откуда 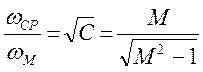 .
.
Тогда 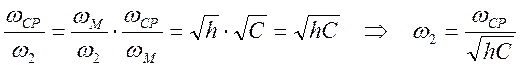 .
.
И, окончательно, 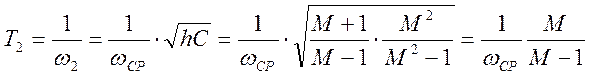 .
.
Кроме того 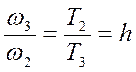 , значит
, значит 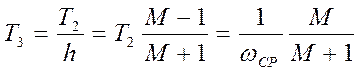 .
.
Осталось связать параметры среднечастотной зоны ЛАХ с w0.
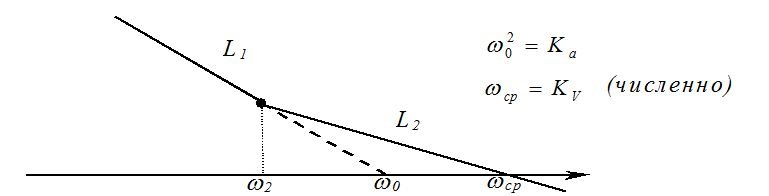
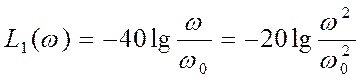 ;
; 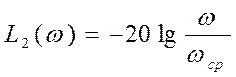 .
.
При w = w2
L1(w2)=L2(w2).
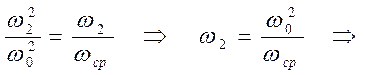
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.