Динамический синтез с использованием запретных зон. Определение параметров среднечастотной зоны желаемой ЛАХ, страница 5

Определим параметры среднечастотной зоны, когда собственная частота колебательного звена относительно низка. Будем полагать (что удобно), что ЛАХ системы в среднечастотной области является симметричной:

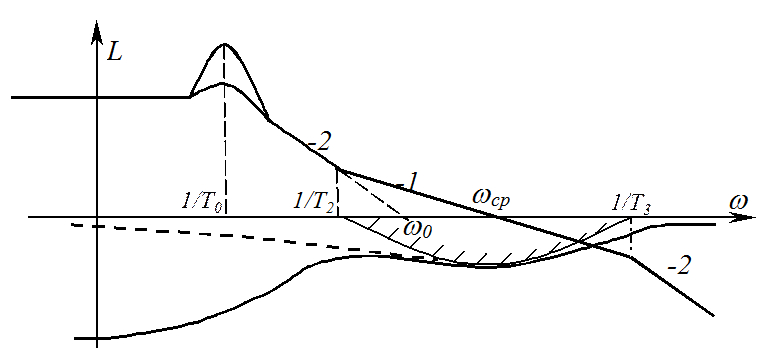
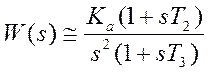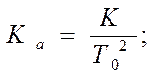
;     .  Тогда в области средних частот передаточная функция системы записывается в приближенном виде:  ;   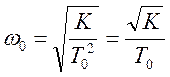     .   В этом случае параметры системы могут быть определены как: 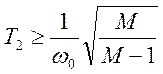  , 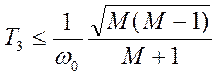 .  Для получения более точных результатов следует воспользоваться формулой:  .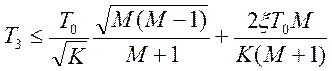

При наличии в системе апериодических звеньев более высоких порядков в приведенных выше формулах следует вместо  положить .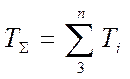

Учет нестабильности параметров в данной системе решается аналогично системе с наклоном ЛАХ в среднечастотной области 2-1-2.

Если в качестве типовой для среднечастотной зоны используется несимметричная ЛАХ (типа 2-1 или 1-2), то решение данной задачи существенно усложняется. При наличии же астатизма в системе - все значительно сложнее.

Расчет среднечастотной области ЛАХ системы

на базе типовой ЛАХ 1-2

(Предварительно перед изучением каждого пункта

следует повторить  материал на стр. 45-46)

1.  Система 1-2-3-4... Системе с такой ЛАХ соответствует передаточная функция   .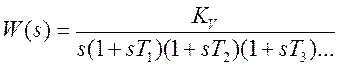

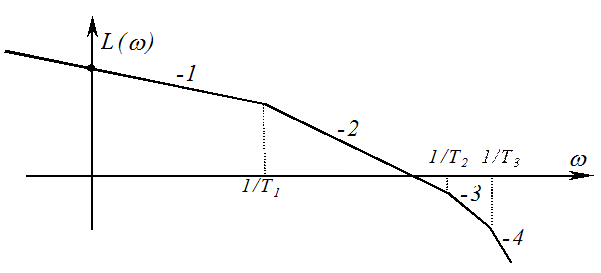
В отличие от системы 1-2 данная система имеет дополнительно апериодические звенья с малыми постоянными времени Т₂, Т₃,…

Для обеспечения требуемых динамических свойств в замкнутой системе должно выполняться ограничение на сумму постоянных времени:  

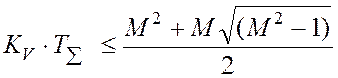,   где

В таких системах показатель колебательности  (не более).

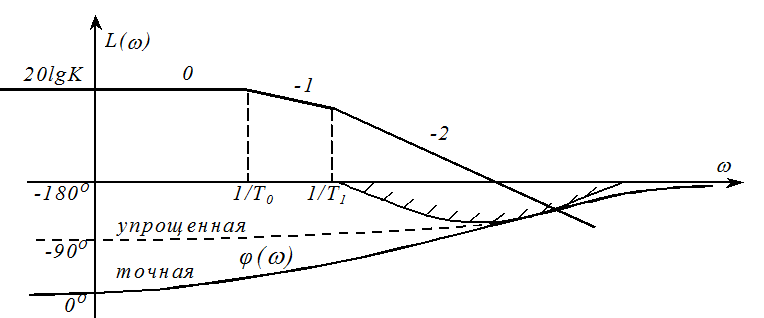
          2. Система 0-1-2.  Данная система является статической системой. В низкочастотной области ЛАХ разомкнутой системы расположена горизонтально, с наклоном 0 дб/дек. Передаточная функция ее имеет вид:

.

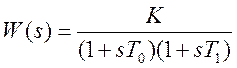Если постоянные времени таковы, что   (что чаще всего и бывает),  то  передаточная функция разомкнутой системы в области средних частот может быть приближенно представлена:  , - получили систему вида 1-2, которой соответствует передаточная функция: 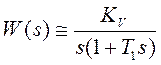 , где 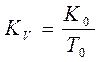   . Значения величин Т₀ и К определяются точностными требованиями к системе.

Для упрощенной системы (1-2) у нас ранее было получено соотношение

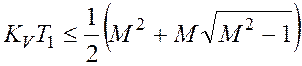, которое для данного случая принимает вид:

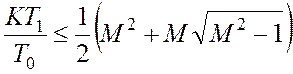, откуда определяется постоянная времени Т₁.

В этой формуле большая постоянная времени Т₀ выполняет стабилизирующую функцию. При переходе от упрощенной системы к точной (исходной) повышается запас устойчивости. Данный факт отчетливо наблюдается на рисунке, где изображены фазовые характеристики статической (точная) и астатической (упрощенная) систем.

3. Система 0-1-2-3-4-... Данная система, как и предыдущая, также является статической.

В ней с целью обеспечения требуемых динамических свойств должно выполняться неравенство:

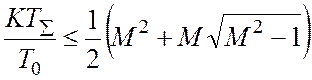,       где     

Как показывает практика, хорошее качество динамических процессов редко удается получить в статических несимметричных ЛАХ. Для этой цели целесообразно в статических системах в области средних частот использовать типовую симметричную ЛАХ с наклонами 2-1-2.

4. Учет нестабильности параметров для системы 1-2

Из предыдущего имеем   ,  .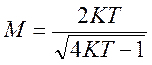

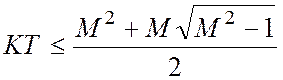Параметры системы, влияющие на ее колебательность, - К и Т.

Функции чувствительности М  по этим параметрам:

,

.

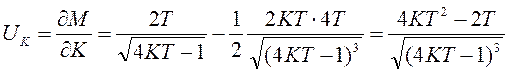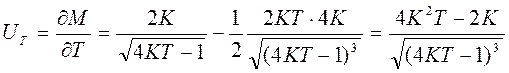Отклонение показателя колебательности М от расчетного значения составит:

.

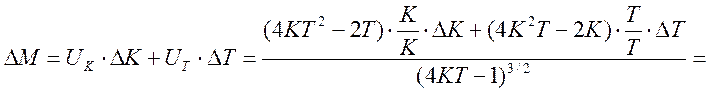
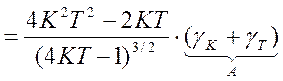Для учета случайного ухода параметров принимается .

Потребуем, чтобы  .  Тогда после подстановки имеем:

.

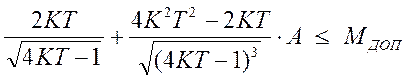Последнее неравенство необходимо решить относительно Т или КТ. Результат можно получить только численно при конкретных значениях А и М_ДОП.

5. Учет нестабильности параметров в системах 1-2-3-4-…, 0-1-2, 0-1-2-3-4-…

Задача учета нестабильности параметров в системах 1-2-3-4…,  0-1-2,  0-1-2-3-4… решается аналогично системе 1-2. С целью обеспечения  в системе  требуемых динамических свойств  получают соответствующие функции чувствительности, выражения для и аналогичное неравенство для нахождения искомой постоянной Т₁.

Получить самостоятельно по аналогии!