«…Действительно, если треугольник АВС совмещается с треугольником DEF и кладутся точка А на точку D, а прямая АВ на DE, то и точка В совместится с Е вследствие того, что АВ равна DE; а так как АВ совместилось с DE, то и прямая АС совместится с DF вследствие того, что угол ВАС равен EDF; так что и точка С совместится с точкой F вследствие того, что АС тоже равно DF …»
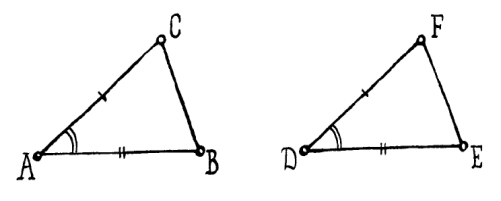
Рис. 1
(Далее Евклид объясняет неизбежность совмещения сторон ВС и ЕF , иначе возникнет противоречие с его первым постулатом; мы бы сказали, что «иначе через две различные точки Е и F пройдут две различные прямые») «…так что и весь треугольник АВС совместится со всем треугольником DEF и будет ему равен…»
Постараемся разобраться: что такое «совмещать»? Видимо, не следует полагать право «совмещать фигуры» как бы заранее данным, ведь речь не идет о треугольных предметах, которые можно брать руками. Надо признать, что «мысленное совмещение» есть поточечное отображение одной фигуры на другую, при котором сохраняются расстояния между парами точек в их образах. Мы будем называть это «движением» плоскости, при котором, в частности, точки А, В, С отобразились соответственно в D, E, F .
Определение. Движением называют такое преобразование плоскости, при котором для любых двух точек А1 и В1 их образы А2 и В2 удовлетворяют условию | А1В1| = | А2В2 |, то есть при движении сохраняются расстояния в их образах.
Термин «движение» в геометрии понимается не механически (во времени), а как отображение исходного состояния в конечное (мгновенно). Образно говоря, в киноленте событий оставляют лишь первый и последний кадры.
§ 1. 1 Простейшие виды движений плоскости
1). Осевая симметрия. Обозначение: Sl (первая буква слова symmetry).
Определение. Осевая симметрия, задаваемая прямой l (осью симметрии) – это преобразование плоскости , для которого всякая точка М1 получает образ М2 так , что прямая l – серединный перпендикуляр к отрезку М1М2.
Осевую симметрию часто называют зеркальной, потому что полуплоскость как бы отражается в зеркале l . В «зазеркалье» левое становится правым.
Неподвижными при симметриии останутся лишь точки оси l .
Замечание. Осевая симметрия является движением.
Докажем это свойство с применением координат. Введем ось Ох декартовой системы вдоль оси симметрии. Пусть образами точек М1(x1, y1) и К1(x3, y3) стали точки М2(x2, y2) и К2(x4, y4) (Рис.2). Зависимость между «новыми» (x2, y2) и «старыми» (x1, y1) значениями координат точки М характеризуется тем, что «икс сохраняется, а игрек меняет знак», что выражается формулами:
|
Рис. 2 |
Система (1) дает правило пересчета координат для образов при осевой симметрии. Зависимость (1) называют аналитическим представлением симметрии. |
В силу выявленной закономерности ( 1 ) используем координаты точек М1, К1 и их образов М2 , К2 для сравнения расстояний
![]() и
и ![]() , убеждаясь в их равенстве.
Значит, симметрия является движением.
, убеждаясь в их равенстве.
Значит, симметрия является движением.
Замечание. Зеркально симметричные фигуры имеют разную ориентацию
|
Рис. 3 |
Математически это можно описать, например, с помощью вращения векторов до их совмещения. В «зеркальных» треугольниках (Рис.3) поворот А1С1 → А1В1 происходит против часовой стрелки , а поворот А2С2 → А2В2 - по часовой стрелке . |
2).Параллельный перенос (вектор). Обозначения: ![]() ,
,
![]() .
.
Определение. Параллельный перенос (либо вектор), задаваемый упорядоченной парой точек А, В – это преобразование плоскости, для которого всякая точка М1 получает образ М2 так, что лучи АВ и М1М2 сонаправлены, а отрезки АВ и М1М2 - равны.
Иначе говоря, все точки плоскости переносятся на одинаковое расстояние в общем направлении.
Неподвижных точек при параллельном переносе нет.
Исключение
составляет лишь нулевой вектор ![]() , равносильный
тождественному преобразованию плоскости.
, равносильный
тождественному преобразованию плоскости.
Замечание. Параллельный перенос является движением.
|
Рис.4 |
Доказательство очевидное: между концами двух равных направленных отрезков расстояние такое же, как и между их началами, потому что они образуют параллелограмм (Рис.4). Формулы пересчета координат при параллельном переносе
говорят о том, что абсциссы всех точек |
меняются на одинаковую величину a,
а ординаты – на b. То есть имеем вектор ![]() с координатами (a, b).
с координатами (a, b).
3).Скользящее отражение (переносная симметрия).Обозначение: ![]() ,
,
![]() .
.
Определение. Скользящее отражение
– это композиция осевой симметрии Sl и параллельного
переноса ![]() при условии, что вектор
при условии, что вектор ![]() и ось симметрии lпараллельны.
и ось симметрии lпараллельны.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.