Движения плоскости. Простейшие виды движений плоскости. Параллельный перенос (вектор). Скользящее отражение, страница 2

Если плоскость рассматривать в пространстве, то симметрия относительно оси будет равносильна повороту вокруг нее на угол 180⁰. Тогда скользящее отражение составиться из такого поворота и параллельного переноса вдоль оси. Образно это напоминает ключ в замочной скважине, который поворачивают, а затем вытаскивают.

Частным случаем скользящего отражения (при нулевом векторе ) является осевая симметрия.

 

 Скользящее отражение при  ненулевом векторе  не имеет ни одной неподвижной точки.

Рис.5

Формулы пересчета координат точек при скользящем отражении наиболее просто выглядят  (3) в декартовой системе с осью Ох вдоль оси симметрии  l :                  (3) Здесь подразумевается, что вектор  имеет координаты (a, 0) (Рис.5).

       4). Поворот плоскости.  Обозначение:   .

Для обозначения берется первая буква слова Round (круг, вокруг). Легко представить себе поворот листа фанеры вокруг вбитого в стену гвоздя.

Частный случай поворота на угол  при нечетном значении k называют центральной симметрией  или  симметрией относительно центра О. При четном значении коэффициента k получится поворот на нулевой угол, то есть тождественное преобразование плоскости.

Поворот на ненулевой угол имеет ровно одну неподвижную точку – центр О.

Рис.6

Доказательство. Пусть при  повороте на угол  вокруг центра О точки К1 и М1 получают образы К2   и  М2  (Рис.6).                    Докажем, что К2М2=К1М1 , путем рассмотрения треугольников ОК2М2 и ОК1М1 . Они равны по первому признаку, т.к. ОК1=ОК2, ОМ1=ОМ2, К1ОМ1=К2ОМ2 (от равных углов  вычитается их общая часть).

Для поворота на угол  обратным преобразованием будет поворот вокруг того же центра, но уже на угол  (-), то есть в обратном направлении.

Рассмотрим изменение координат точек при повороте вокруг начала декартовой системы.

Рис. 7

Пусть при повороте на угол  точка М1, имевшая  координаты  x1, y1  , отобразилась в точку М2 с координатами   x2,  y2  (Рис.7) . Найдем зависимость «новых» значений координат от «старых». В прямоугольных треугольниках катеты x  иy определяются равными гипотенузами  ОМ1=ОМ2=r.  Поэтому х 1= ОМ1 cos φ           х2 = ОМ2 cos(φ+α)       y 1= OM1 sin φ            y2 = ОМ2 sin(φ+α)

Используя формулы сумм косинуса и синуса, в выражениях х₂ = ρ cos(φ+α) = ρcos φ cos α - ρsin φ sin α

y₂ = ρ sin(φ+α) = ρcos φ sin α + ρsin φ cos α

заменим компоненты      ρcos φ=x₁ ,         ρsin φ=y₁       и   получим

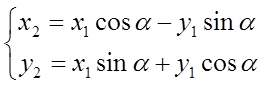                   (4)

(аналитическое представление поворота вокруг начала координат).

           Пример. При повороте плоскости на угол α=π/6 вокруг начала координат точка М₁(4,2) отобразится в некоторую точку М₂, координаты которой x₂, y₂  легко найти из формул (4) непосредственной подстановкой в правую часть значений x₁=4,  y₁=2, α=π/6 . После вычислений получим x₂=2-1,  y₂=2+,     то есть   .

§ 1. 2.  Общие  свойства  движений  плоскости

Нужно доказать, что если точки А₁ и В₁ отображаются  в А₂ и В₂, то образы всех точек, лежащих между А₁ и В₁  заполнят внутренность отрезка [А₂В₂].

Доказательство. Пусть некоторая точка С₁ лежит между А₁ и В₁ (Рис.8), тогда А₁С₁ + С₁В₁ =  А₁В₁. По определению, при движении сохраняются расстояния между точками в их образах.   Поэтому после замены в формуле величин на соответственно равные им  А₂С₂ , С₂В₂  и  А₂В₂  получим  новое  соотношение