Движения плоскости. Простейшие виды движений плоскости. Параллельный перенос (вектор). Скользящее отражение, страница 5

В §1.1 обсуждались  виды движений, которые мы условно называли «простейшими». Они  качественно отличаются, причем по разным признакам. Например, поворот имеет неподвижную точку, а параллельный перенос не имеет.

Оказывается, в природе вообще нет других типов движений, т.е. любое движение (хотя бы и полученное сложной композицией) будет равносильно одному из ранее названных «простейшими». Сейчас мы это строго докажем. 

Доказательство. Ранее мы выяснили, что всякое  движение задается парой конгруэнтных  треугольников.  Движение  первого рода  сохраняет  ориентацию фигур, а, значит, определяется парой равных треугольников. Помня об этом, достаточно следить при отображении лишь за парой соответственных сторон образа и прообраза, например, А₁В₁ и А₂В₂ (Рис.13).

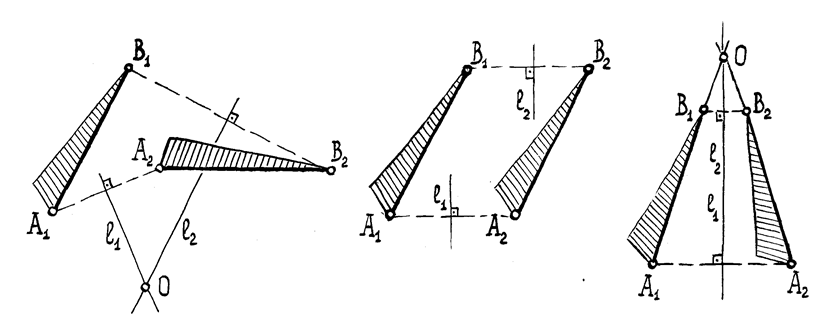
Рис.13                      (а)                                              (б)                                          (в)

Тривиальный случай (совпадение этих отрезков) означал бы тождественное преобразование.

Если бы выполнялось , то  отрезки задавали бы параллельный перенос плоскости. Пусть . Покажем, что отрезки можно совместить поворотом. Т.к. при повороте точки и ее образ лежат на общей окружности с центром О, то этот центр должен принадлежать серединному перпендикуляру l₁ к отрезку А₁А₂. С другой стороны, этот центр принадлежит к серединному перпендикуляру l₂, к отрезку В₁В₂. Если = 0, то это искомый центр поворота (Рис.13, а).

Случай l₁ || l₂ соответствует параллельному переносу (Рис.13, б).

Если же прямые l₁  и  l₂  совпадают, то  на пересечении l₁  и А₁В₁  найдется снова центр поворота (Рис.13, в). Таким образом, два равных отрезка (а, значит, и два равных треугольника) удастся совместить «за один этап» (параллельный перенос либо поворот вокруг подходящего центра). Ч.т.д.

        Пример. Пусть известно, что некоторое движение сохраняет ориентацию фигур и имеет ровно одну неподвижную точку. Что можно о нем сказать? Ответ следует из теоремы Шаля: речь идет о движении первого рода, но не о параллельном переносе (у которого нет неподвижных точек) и не о тождественном преобразовании (у которого их бесконечно много). Значит, это движение – поворот.

        Доказательство. Движение второго рода будет задано парой конгруэнтных

треугольников с  разной ориентацией .  Продемонстрируем на чертеже, как для них восстановить ось скользящего отражения (Рис.14).

Построив ось скользящего отражения, мы тем самым доказали теорему.

      Пример. Если некоторое движение второго рода не имеет неподвижных точек, то оно является скользящим отражением. Если же имеет хоть одну неподвижную точку, то является осевой симметрией.

Можно говорить, что мы провели полную классификацию движений. Отразим эти результаты в таблице 1, обращая особое внимание на наличие неподвижных точек  отображения  (это понадобится  в дальнейших рассуждениях).  Кроме того, бывают ситуации,  когда неподвижных точек  может не быть,  но найдется какая-нибудь прямая, точки которой отобразились в точки этой же прямой. Такую прямую будем называть инвариантной (неизменной). Например, прямая может параллельно переноситься вдоль себя, сохраняя свое положение на плоскости. Образное сравнение: молекулы воды переместились, но русло реки сохранилось (оно инвариантно). Другой пример: при повороте на угол 180⁰ вокруг своей точки прямая переходит в себя, то есть остается инвариантной.

Таблица 1 систематизирует всевозможные движения плоскости. Любое другое движение при внимательном рассмотрении совпадет с одним из указанных.