В результате измерений получена выборка x1, x2, …, xN из генеральной совокупности с неизвестным законом распределения.
1. Построить:
1.1. Выборочную функцию распределения F(x);
1.2. Гистограмму
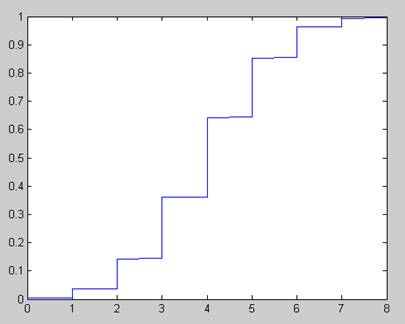
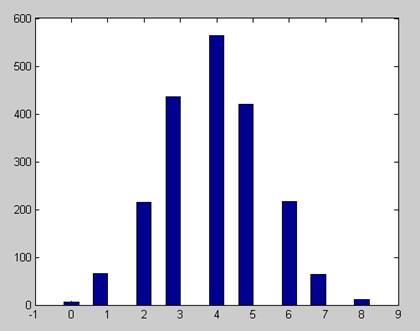
Рис 1: выборочная функция распределения Рис 2: Гистограмма
2. Вычислить:
2.1. Точечные оценки:
2.1.1. моментов
· первого начального:
математическое ожидание, среднее арифметическое:
|
|
![]()
|
![]()
· центральных моментов:
второй:
|
|
третий:
|
|
![]()
· определить моду: xmod = 4 (распределение одномодальное симметричное, мода совпадает с выборочной медианой и средним арифметическим)
2.1.2. асимметрии и эксцесса:
|
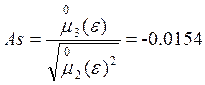
|
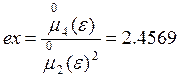
2.1.3. границ интерквантильного промежутка для P = 0.95 только по полной выборке:
Jp=SX((1+0.95)/2*N)
Jq=SX(0.05/2*N)
[1,7] – границы интерквантильного промежутка
2.1.4. характеристики по п. 2.1.1-2.1.2 по отдельным частям выборки, содержащим по N/10 значений (всего 10 частичных выборок):
|
|
|
|
|
|
|
|
|
|
|
|
N |
4,005 |
4 |
4 |
2,017 |
1,4202 |
0,14875 |
11,41 |
0,051927 |
2,8046 |
|
N/10 |
4,02 |
4 |
4 |
1,7896 |
1,3378 |
-0,23738 |
7,6247 |
-0,099156 |
2,3807 |
|
N/10 |
4,075 |
4 |
4 |
2,0794 |
1,442 |
0,20672 |
12,633 |
0,068941 |
2,9217 |
|
N/10 |
3,915 |
4 |
4 |
2,0878 |
1,4449 |
0,358 |
13,226 |
0,11867 |
3,0344 |
|
N/10 |
4,095 |
4 |
4,5 |
2,196 |
1,4819 |
0,54829 |
13,518 |
0,16849 |
2,8032 |
|
N/10 |
4,035 |
4 |
3,5 |
1,9938 |
1,412 |
-0,024389 |
10,804 |
-0,0086633 |
2,7178 |
|
N/10 |
4,01 |
4 |
4,5 |
1,8399 |
1,3564 |
0,2248 |
9,4499 |
0,090076 |
2,7915 |
|
N/10 |
3,785 |
4 |
4 |
2,1088 |
1,4522 |
-0,1349 |
11,832 |
-0,044053 |
2,6607 |
|
N/10 |
4,075 |
4 |
4,5 |
1,7194 |
1,3112 |
-0,012281 |
8,6306 |
-0,0054474 |
2,9194 |
|
N/10 |
4,03 |
4 |
4,5 |
2,0491 |
1,4315 |
0,62555 |
11,924 |
0,21327 |
2,8398 |
|
N/10 |
4,01 |
4 |
4 |
2,2299 |
1,4933 |
0,033102 |
13,207 |
0,0099409 |
2,6561 |
Представить эти же результаты графически:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
2.2. Интервальные оценки с доверительной вероятностью Q=0,8:
· первого начального и второго центрального моментов (по полной выборке и по отдельным частям)
интервальная оценка первого начального момента по полной выборке:
![]()
|
|
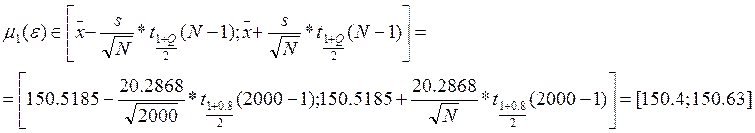
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.