Моделирование системы диагностирования, построенной с использованием структурных инвариантов

Санкт-Петербургский Государственный Политехнический Университет

__________________________________________________________________

Факультет Технической Кибернетики

Компьютерных Систем и Программных Технологий

Отчет

по лабораторной работе №3

Моделирование системы диагностирования, построенной с использованием структурных инвариантов

Работу выполнил: Ульзутуев П.С.

группа 5081/10

Преподаватель: Сабонис С.С.

Санкт-Петербург

2011

1.  Осуществить построение структурных инвариантов, заданных в следующем виде:

1.1.  Разность одноименных параметров различных ИК.

clear all

count = 5000;   % число измерений

M = 0;          % значение мат. ожидания

D = 3;          % значение дисперсии

Dfm = 2500;     % момент возникновения неисправности

T = 1:count;     

for i=1:count

    if (i < Dfm)

        base1(i) = normrnd(0,1);

        base2(i) = normrnd(0,1);

        base3(i) = normrnd(0,1);

    else

        base1(i) = normrnd(M,D);

        base2(i) = normrnd(0,1);

        base3(i) = normrnd(0,1);

    end

    % Инвариант

    delta12(i) = base1(i) - base2(i);

    delta13(i) = base1(i) - base3(i);

    delta23(i) = base2(i) - base3(i);

    % Оценка инварианта

    mu1(i) = mean(delta12);

    mu2(i) = mean(delta13);

    mu3(i) = mean(delta23);

    d1(i) = std(delta12);

    d2(i) = std(delta13);

    d3(i) = std(delta23);

end

figure

subplot(3,1,1);

plot(T,base1,'b');

ylabel('y1');

subplot(3,1,2);

plot(T,base2,'r');

ylabel('y2');

subplot(3,1,3);

plot(T,base3,'g');

xlabel('t');

ylabel('y3');

figure

% Оценка мат. ожидания

subplot(2,1,1);

plot(T,mu1,'b',T,mu2,'r',T,mu3,'g');

ylabel('M');

% Оценка дисперсии

subplot(2,1,2);

plot(T,d1,'b',T,d2,'r',T,d3,'g');

xlabel('t');

ylabel('D');

Результаты:

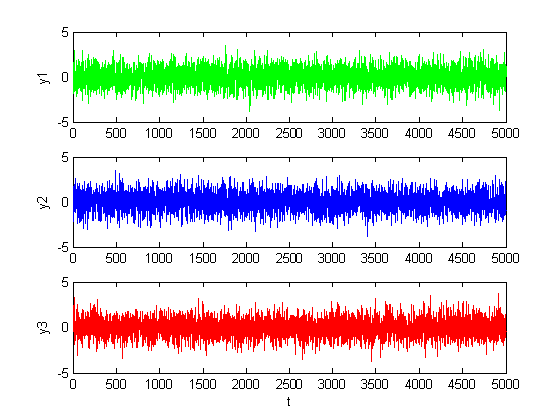
                                    Рис. 1.1.1. Графики сигналов в каналах при отсутствии дефектов (M = 0, D = 1).                       

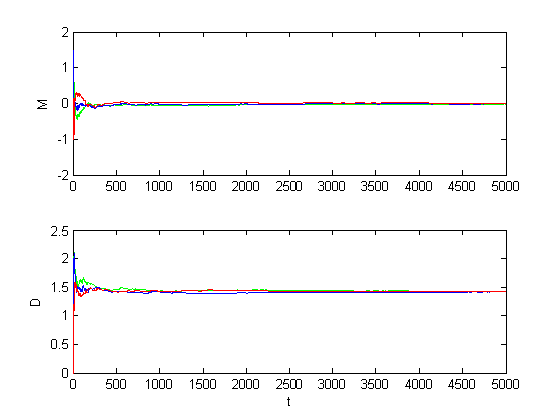
Рис. 1.1.2. Графики оценок инвариантов при отсутствии дефектов (M = 0, D = 1).

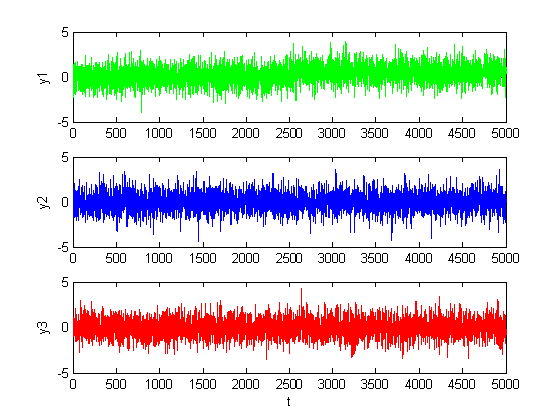
Рис. 1.1.3. Графики сигналов в каналах при малом сдвиге (M = 0.5, D = 1).

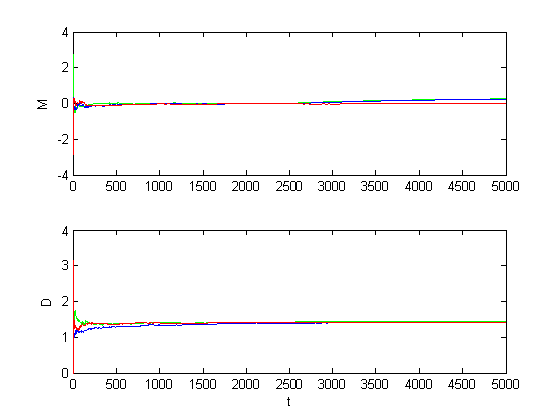
Рис. 1.1.4. Графики оценок инвариантов при малом сдвиге (M = 0.5, D = 1).

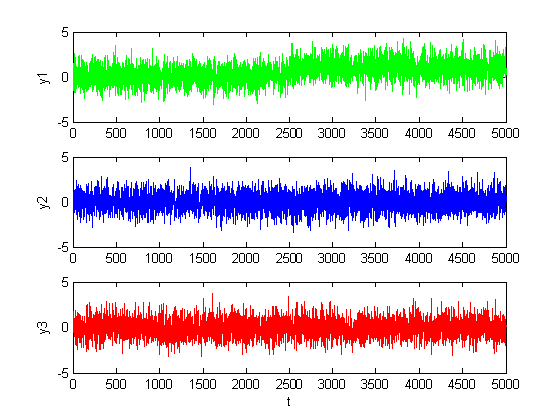
Рис. 1.1.5. Графики сигналов в каналах при среднем сдвиге (M = 1, D = 1).

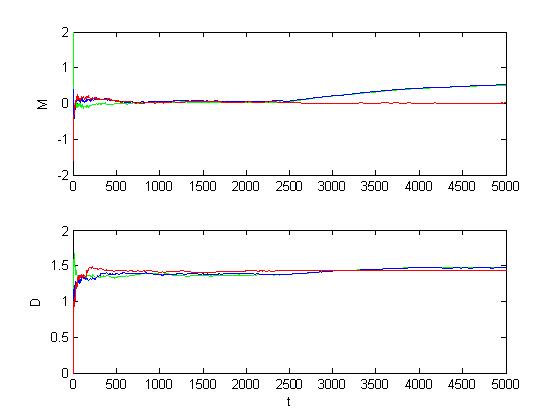
Рис. 1.1.6. Графики оценок инвариантов при среднем сдвиге (M = 1, D = 1).