delta3(i) = base3(i) - median(cat(2,base1(i), base2(i), base3(i)));
% Оценка инварианта
mu1(i) = mean(delta1);
mu2(i) = mean(delta2);
mu3(i) = mean(delta3);
d1(i) = std(delta1);
d2(i) = std(delta2);
d3(i) = std(delta3);
end
figure
subplot(3,1,1);
plot(T,base1,'g');
ylabel('y1');
subplot(3,1,2);
plot(T,base2,'b');
ylabel('y2');
subplot(3,1,3);
plot(T,base3,'r');
xlabel('t');
ylabel('y3');
figure
% Оценка мат. ожидания
subplot(2,1,1);
plot(T,mu1,'g',T,mu2,'b',T,mu3,'r');
ylabel('M');
% Оценка дисперсии
subplot(2,1,2);
plot(T,d1,'g',T,d2,'b',T,d3,'r');
xlabel('t');
ylabel('D');
Результаты:
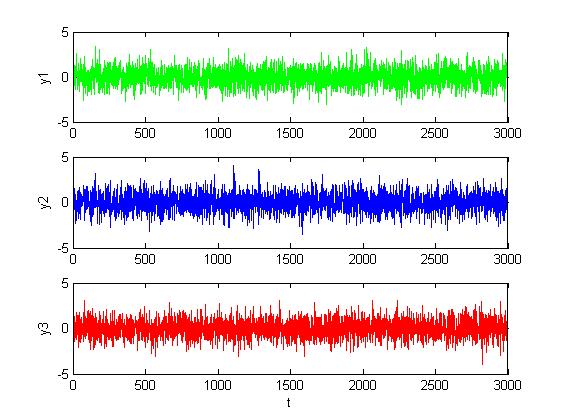
Рис. 1.3.1. Графики сигналов в каналах при отсутствии дефектов (M = 0, D = 1).
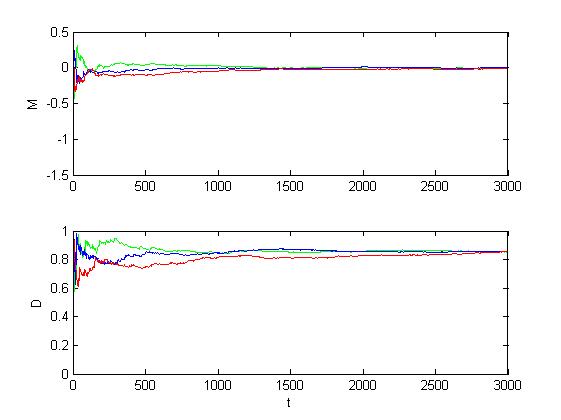
Рис. 1.3.2. Графики оценок инвариантов при отсутствии дефектов (M = 0, D = 1).
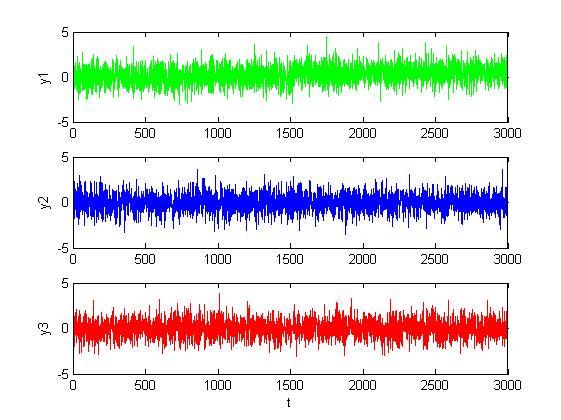
Рис. 1.3.3. Графики сигналов в каналах при малом сдвиге (M = 0.5, D = 1).
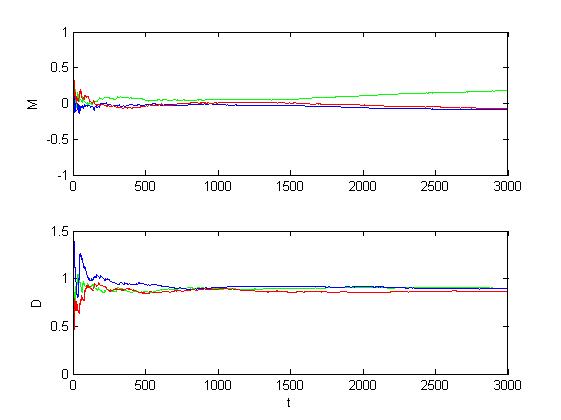
Рис. 1.3.4. Графики оценок инвариантов при малом сдвиге (M = 0.5, D = 1).
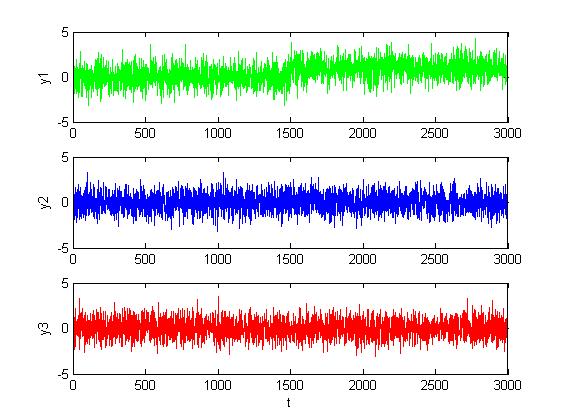
Рис. 1.3.5. Графики сигналов в каналах при среднем сдвиге (M = 1, D = 1).
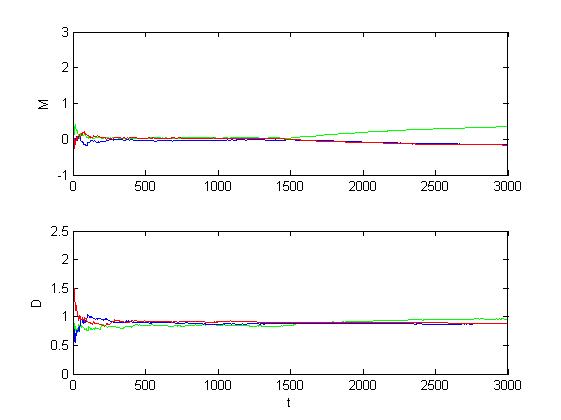
Рис. 1.3.6. Графики оценок инвариантов при среднем сдвиге (M = 1, D = 1).
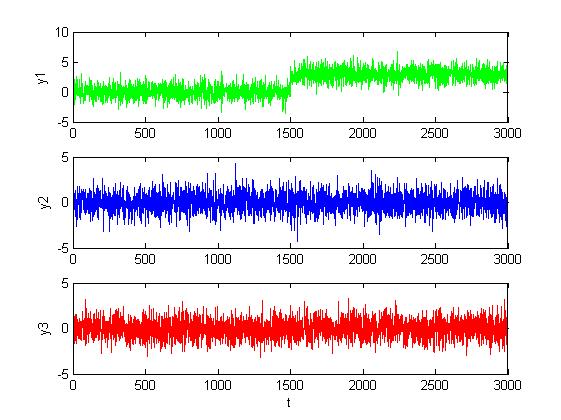
Рис. 1.3.7. Графики сигналов в каналах при большом сдвиге (M = 3, D = 1).
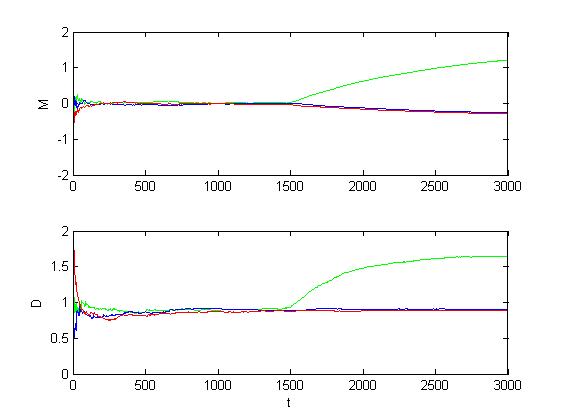
Рис. 1.3.8. Графики оценок инвариантов при большом сдвиге (M = 3, D = 1).
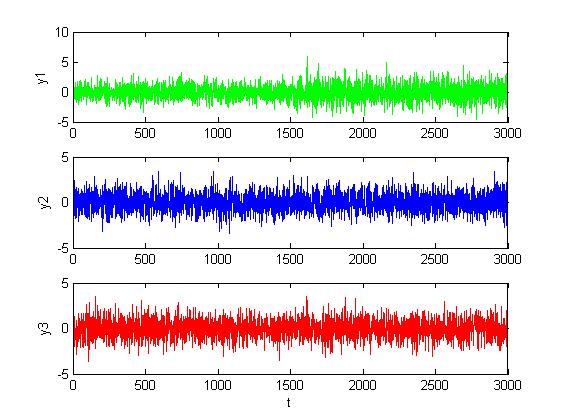
Рис. 1.3.9. Графики сигналов в каналах при малом изменении уровня шумов
(M = 0, D = 1.5).
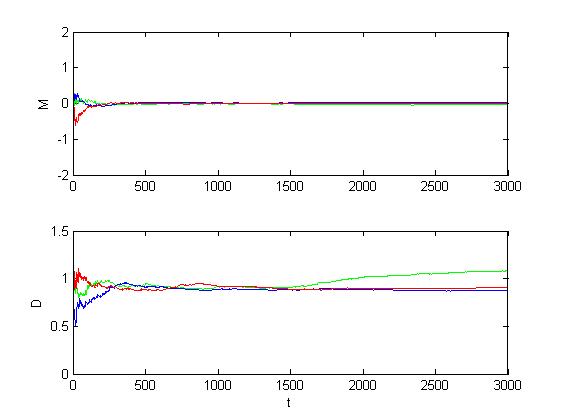
Рис. 1.3.10. Графики оценок инвариантов при малом изменении уровня шумов
(M = 0, D = 1.5).
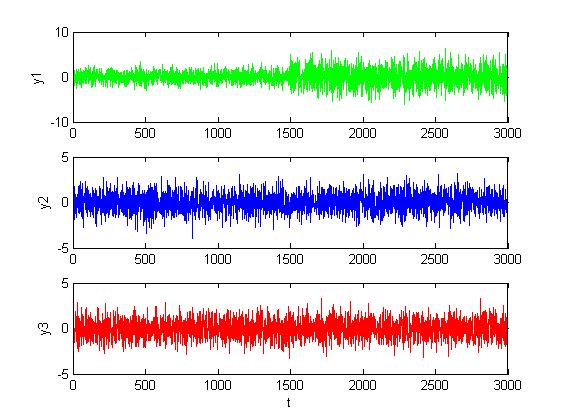
Рис. 1.3.11. Графики сигналов в каналах при среднем изменении уровня шумов
(M = 0, D = 2).
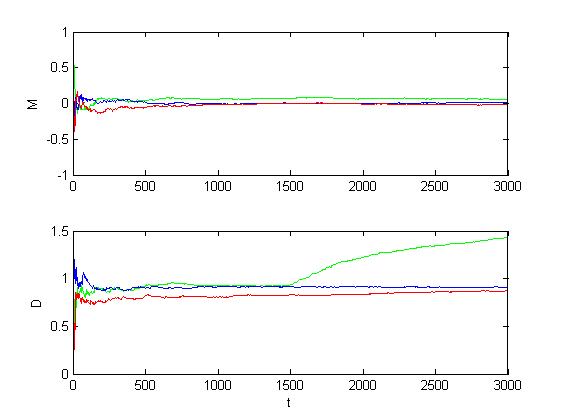
Рис. 1.3.12. Графики оценок инвариантов при среднем изменении уровня шумов
(M = 0, D = 2).
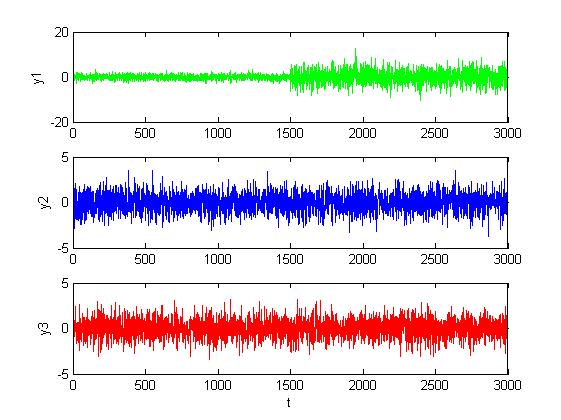
Рис. 1.3.13. Графики сигналов в каналах при большом изменении уровня шумов
(M = 0, D = 3).
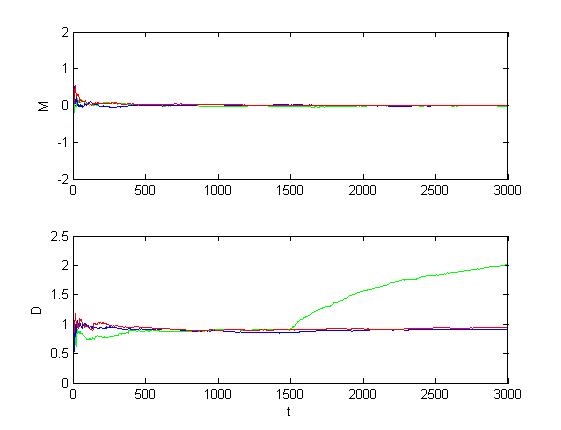
Рис. 1.3.14. Графики оценок инвариантов при большом изменении уровня шумов
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.