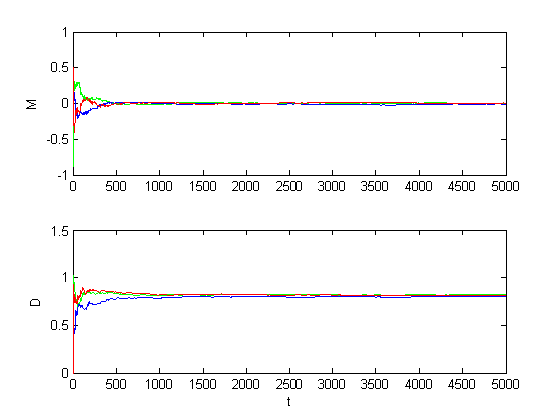
Рис. 1.2.2. Графики оценок инвариантов при отсутствии дефектов (M = 0, D = 1).
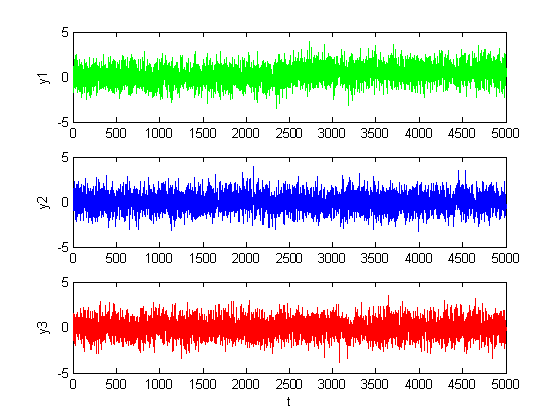
Рис. 1.2.3. Графики сигналов в каналах при малом сдвиге (M = 0.5, D = 1).
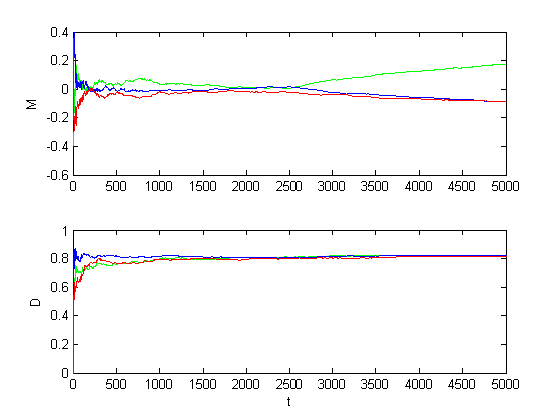
Рис. 1.2.4. Графики оценок инвариантов при малом сдвиге (M = 0.5, D = 1).
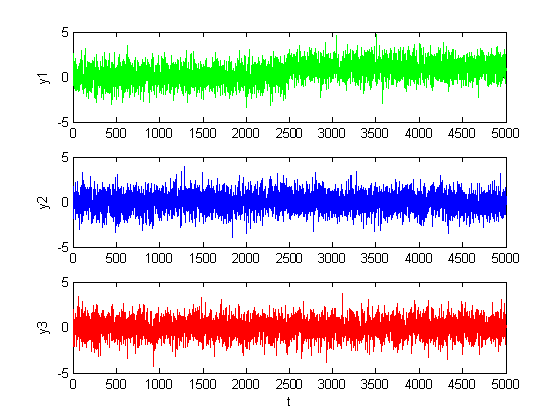
Рис. 1.2.5. Графики сигналов в каналах при среднем сдвиге (M = 1, D = 1).
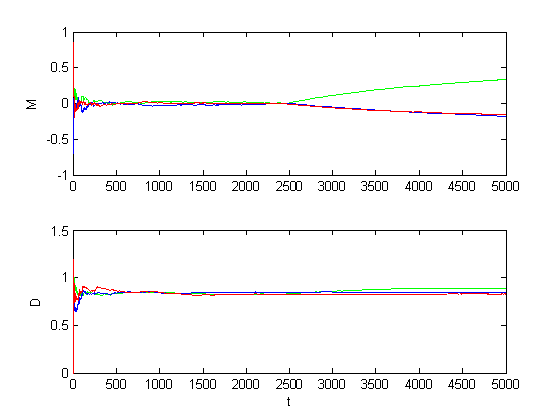
Рис. 1.2.6. Графики оценок инвариантов при среднем сдвиге (M = 1, D = 1).
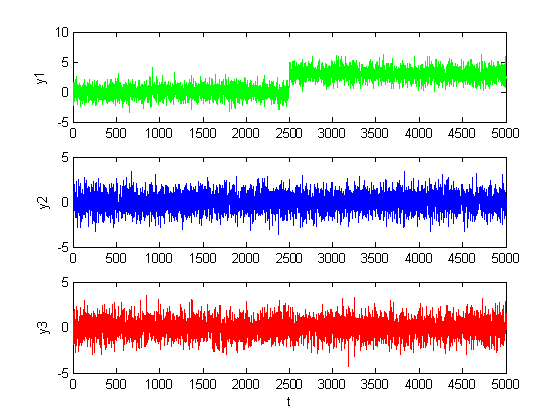
Рис. 1.2.7. Графики сигналов в каналах при большом сдвиге (M = 3, D = 1).
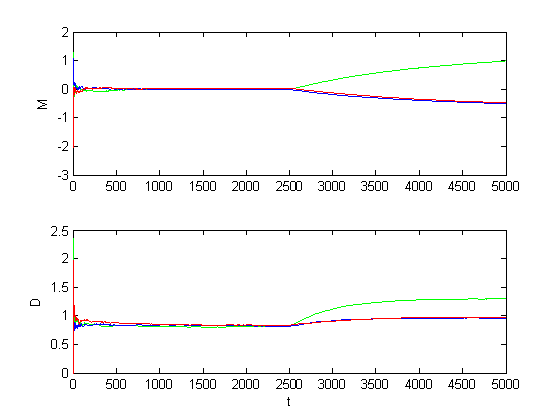
Рис. 1.2.8. Графики оценок инвариантов при большом сдвиге (M = 3, D = 1).
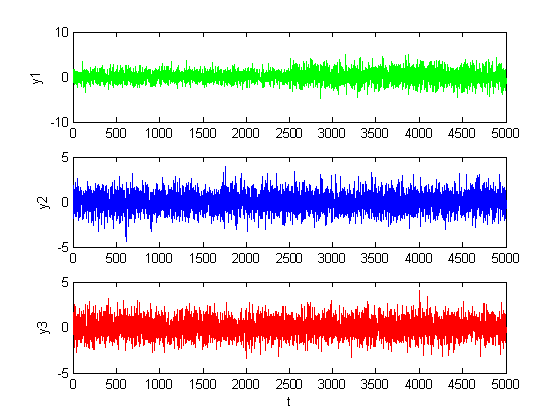
Рис. 1.2.9. Графики сигналов в каналах при малом изменении уровня шумов
(M = 0, D = 1.5).
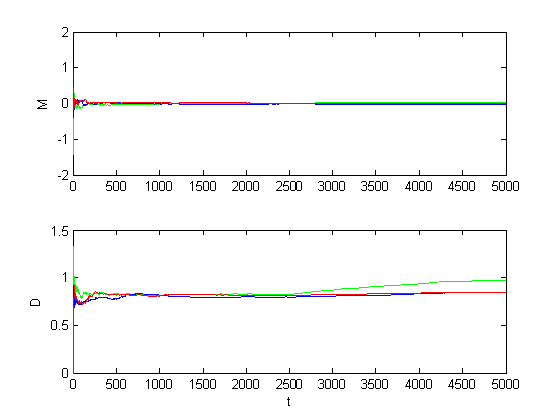
Рис. 1.2.10. Графики оценок инвариантов при малом изменении уровня шумов
(M = 0, D = 1.5).
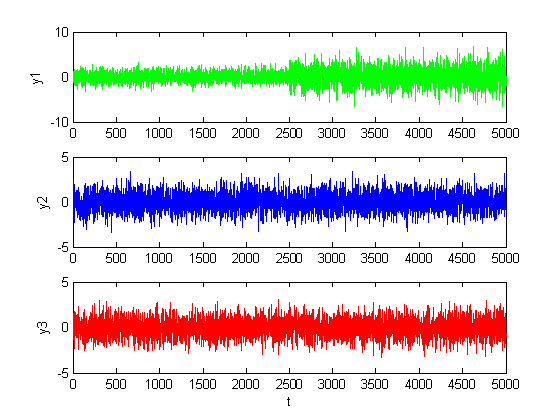
Рис. 1.2.11. Графики сигналов в каналах при среднем изменении уровня шумов
(M = 0, D = 2).
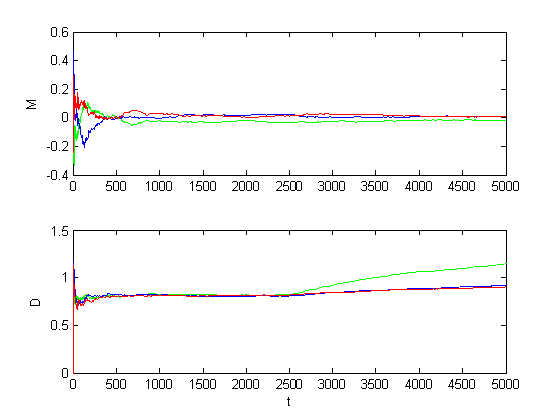
Рис. 1.2.12. Графики оценок инвариантов при среднем изменении уровня шумов
(M = 0, D = 2).

Рис. 1.2.13. Графики сигналов в каналах при большом изменении уровня шумов
(M = 0, D = 3).
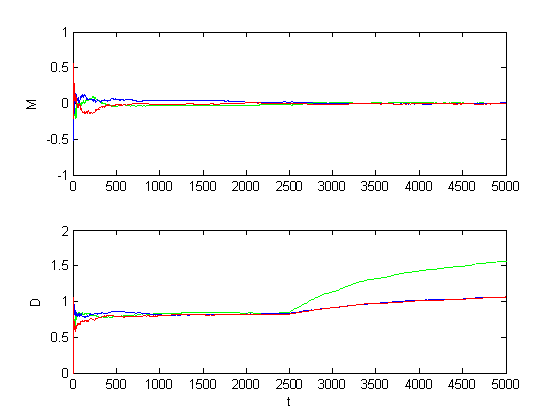
Рис. 1.2.14. Графики оценок инвариантов при большом изменении уровня шумов
(M = 0, D = 3).
1.3. Разность между параметрами ИК и порядковым средним.
clear all
count = 3000; % число измерений
M = 0; % значение мат. ожидания
D = 1; % значение дисперсии
Dfm = 1500; % момент возникновения неисправности
T = 1:count;
for i=1:count
if (i < Dfm)
base1(i) = normrnd(0,1);
base2(i) = normrnd(0,1);
base3(i) = normrnd(0,1);
else
base1(i) = normrnd(M,D);
base2(i) = normrnd(0,1);
base3(i) = normrnd(0,1);
end
% Инвариант
delta1(i) = base1(i) - median(cat(2,base1(i), base2(i), base3(i)));
delta2(i) = base2(i) - median(cat(2,base1(i), base2(i), base3(i)));
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.