Санкт-Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Автоматики и Вычислительной Техники
Расчетное задание
по
Теории вероятностей
Работу выполнил студент группы 2081/1
Ульзутуев П.С.
Преподаватель: Никитин Кирилл Вячеславович
________________________________
Санкт-Петербург
2009
Партия из N=100 тензорезисторов подвергается выборочному контролю с разрушением. Партия бракуется, если из m=18 наудачу выбранных тензорезисторов хотя бы один не удовлетворяет требованиям технических условий. Какова вероятность забраковать партию тензорезисторов, если она содержит k=0.08% дефектных.
Решить задачу сначала точно. Затем аппроксимировать процедуру выбора тензорезисторов а) биномиальным распределением и б) распределением Пуассона и получить приближенное решение. Сравнить точные и приближенные ответы и объяснить различие.
1. Точное решение
Вероятность забраковать партию p=1-q, где q-вероятность ее не забраковать.
p=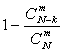 =
=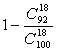 =0.8084697
=0.8084697
2. Аппроксимация биномиальным распределением
Вероятность не выбрать ни одного бракованного элемента:
Q(n)=![]() =
= ![]() =0.2229364
=0.2229364
где n=0-число выбранных бракованных, N=18-число попыток, q=1-p=0.92- вероятность не выбрать бракованный элемент при одной попытке.
P(n)=1-Q(n)=0.7770636
3. Аппроксимацияраспределением Пуассона
Вероятность не выбрать ни одного бракованного элемента:
Q(x)=![]() =
= ![]() =0.2369278
=0.2369278
Вероятность забраковать партию:
P(x)=1-Q(x)=0.7630722
Вывод:
Результаты точных и приближенных вычислений отличаются не более чем на 5.6%, что говорит о высокой степени точности использованных распределений для описания процессов в подобных условиях.
Передаче по каналу связи с равной вероятностью подлежат кодовые слова X1, X2, X3, X4. Канал симметричный, вероятность искажения каждого отдельного символа равна q. В результате однократной передачи на приемной стороне принято слово Y1. В результате повторной передачи того же слова на приемной стороне принято слово Y2. В результате последней (третьей) передачи того же слова на приемной стороне принято слово Y3.
Для исходного ансамбля (X1,X2,X3,X4) рассчитать:
Рассмотреть три передачи как одну передачу слова утроенной длины (кодовые слова X1X1X1, X2X2X2, X3X3X3, X4X4X4, на выходе Y1Y2Y3). Рассчитать
Графически представить априорные и апостериорные распределения возможных сообщений (на одном графике) для первого и второго случая. Проанализировать результаты с точки зрения здравого смысла
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.