Биномиальное распределение и распределение Пуассона (Отчет по расчетному заданию), страница 2

Часть 3

3.1.

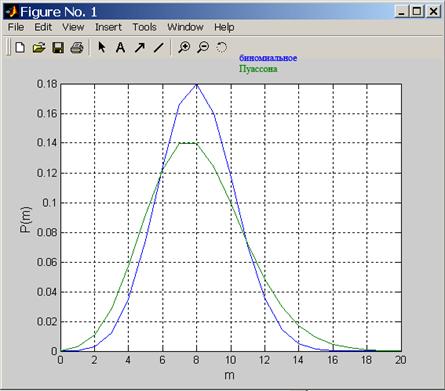
Рассчитать и представить на одном графике биномиальное распределение и распределение Пуассона для различных вариантов np и n.

np	n	p
8	20 и 300	0.2

3.1.1.

n=20;

np=8;

p=np/n;

q=1-p;

for m=0:20

y1=nchoosek(20,m)*((p).^(m))*((q).^(20-m));

y2=((np).^(m))/factorial(m)*exp(-np);

if m==0

vect1=y1;

vect2=y2;

else

vect1=[vect1 y1];

vect2=[vect2 y2];

end

end

plot ((0:20),vect1, (0:20), vect2), grid

xlabel('m', 'Fontsize',12); ylabel('P(m) ', 'Fontsize',12) ;

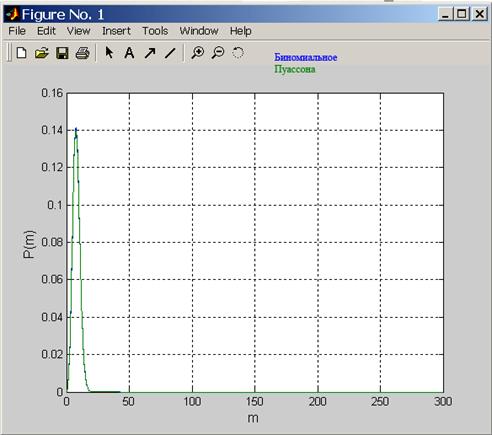
3.1.2.

n=300;

np=8;

p=np/n;

q=1-p;

for m=0:n

y1=nchoosek(n,m)*((p).^(m))*((q).^(n-m));

y2=((np).^(m))/factorial(m)*exp(-np);

if m==0

vect1=y1;

vect2=y2;

else

vect1=[vect1 y1];

vect2=[vect2 y2];

end

end

plot ((0:n),vect1, (0:n), vect2), grid

xlabel('m', 'Fontsize',12); ylabel('P(m) ', 'Fontsize',12) ;

3.2.

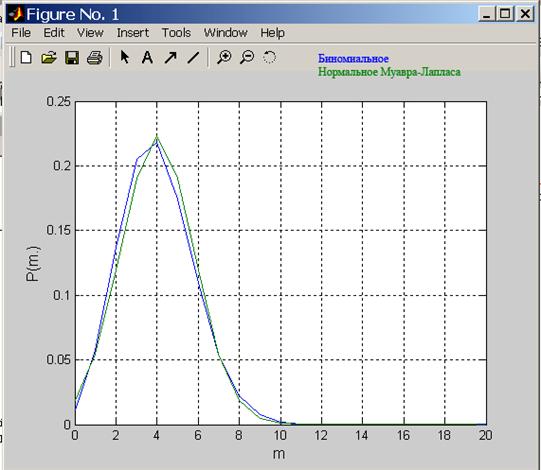
Рассчитать и представить на одном графике биномиальное и аппроксимирующее его по теореме Муавра - Лапласа нормальное распределение для различных вариантов n и p.

3.2.1

n=20;

p=0.2;

q=1-p;

for m=0:n  

y1=nchoosek(n,m)*((p).^(m))*((q).^(n-m));

x=(m-n*p)/sqrt(n*p*q);

fi=exp(-((x).^2)/2)/sqrt(2*pi);

y2=fi/sqrt(n*p*q);

if m==0

vect1=y1;

vect2=y2;

else

vect1=[vect1 y1];

vect2=[vect2 y2];

end

end

plot ((0:n),vect1, (0:n), vect2), grid

xlabel ('m', 'FontSize', 12) ; ylabel (' P(m.) ', 'FontSize', 12) ;

3.2.2.

n=300;

p=0.2;

q=1-p;

for m=0:n  

y1=nchoosek(n,m)*((p).^(m))*((q).^(n-m));

x=(m-n*p)/sqrt(n*p*q);

fi=exp(-((x).^2)/2)/sqrt(2*pi);

y2=fi/sqrt(n*p*q);

if m==0

vect1=y1;

vect2=y2;

else

vect1=[vect1 y1];

vect2=[vect2 y2];

end

end

plot ((0:n),vect1, (0:n), vect2), grid

xlabel ('m', 'FontSize', 12) ; ylabel (' P(m.) ', 'FontSize', 12) ;

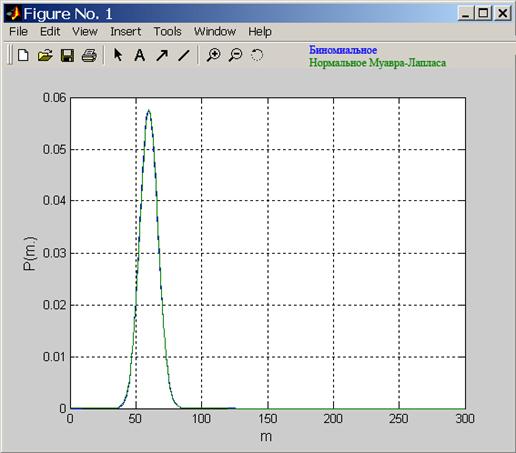
Вывод:

Использованные распределения совпадают тем сильнее, чем больше n.