Массив выборочных значений. Интервальные оценки с доверительной вероятностью. Выборочная функция распределения

Выборочную функцию распределения F(x) (она должна быть ступенчатой!!!)

1.2. Гистограмму

2. Вычислить:

2.1. Точечные оценки:

2.1.1. моментов:

·  первого начального,

·  центральных моментов: второго, третьего, четвертого по выборочной функции распределения.

Для оценки первого начального момента использовать среднее арифметическое, выборочную медиану, средину размаха. Определить моду.

2.1.2. асимметрии и эксцесса;

2.1.3. границ интерквантильного промежутка для P=0.95 только по полной выборке; 2.1.4. характеристики по пп. 2.1.1-2.1.2 по отдельным частям выборки, содержащим по N/10 значений (всего 10 частичных выборок). (!!!! Подвыборки должны быть взяты из неотсортированной изначальной выборки)

Результаты представить в таблице следующей формы.

					s			As	Ex
N
N/10
N/10
…
N/10

Представить эти же результаты графически точками на осях с указанием масштаба на этих осях по форме:

2.2. Интервальные оценки с доверительной вероятностью Q=0.8:

·  первого начального и второго центрального моментов (вычисления выполнить по полной выборке и по отдельным частям, как в п. 2.1.4 - по N/10 значений в каждой частичной выборке).

·  интерквантильного промежутка J для P=0.95:

o  по всей выборке с помощью непараметрических толерантных пределов, симметричных и несимметричных относительно среднего арифметического

o  по частичным выборкам с помощью параметрических толерантных пределов, считая закон распределения генеральной совокупности нормальным.

Результаты представить только графически аналогично тому, как описано выше – под графическим представлением соответствующей точечной оценки, предусмотрев для каждого варианта расчета отдельную ось.

Графическое представление толерантных пределов — также на отдельных осях для каждого варианта. Все оси обозначить.

3. Идентифицировать закон распределения и выбрать подходящий методом проб, определяя параметры закона (если моменты параметрами не являются) и проверяя для КАЖДОЙ пробы гипотезу о соответствии предполагаемого закона распределения экспериментальным данным с помощью ТРЕХ критериев:

"хи-квадрат",     Колмогорова-Смирнова,     "омега-квадрат".

Для начальной ориентировки в выборе закона использовать вид гистограммы, соотношения между моментами и полученные значения эксцесса и асимметрии. Многие теоретические сведения можно найти в интернете по адресу http://ru.wikipedia.org/wiki/Распределение_вероятностей

Зам. В отчете отобразить все ваши пробы относительно выбора подходящего закона распределения, а не одну последнюю (наиболее подходящую).

Подсказка к п.3 – возможные распределения:

Дискретные – биномиальное,  геометрическое, гипергеометрическое, отрицательное биномиальное, Пуассона, равномерное

Непрерывные – арксинус, треугольное, Симпсона, Хи-квадрат, экспоненциальное, нормальное, равномерное, Стьюдента, бета, гамма.

Решение:

1.1  . Выборочная функция распределения F(x).

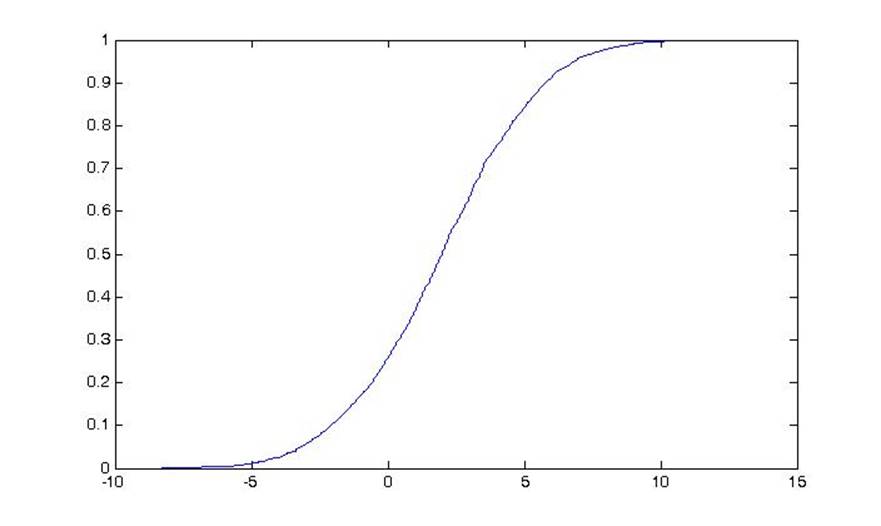
1.2  Гистограмма.

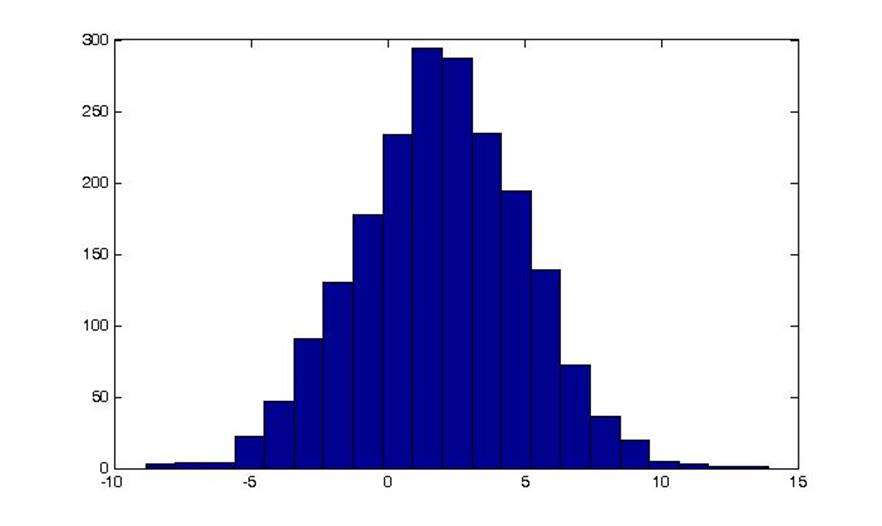
2.1.1 Первый начальный момент.

Выборочная медиана: .

Середина размаха: .

Второй центральный момент:

.

Среднеквадратическое отклонение: .

Третий центральный момент:

Четвертый центральный момент:

Для данного распределения мода совпадает со средним арифметическим и выборочной медианой. .

2.1.2.Асимметрия: .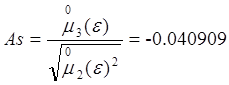

Эксцесс: .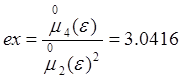

2.1.3Границы интерквантильного промежутка при P=0.95:  J_p=[ -4.0392 ; 7.8061]  

2.1.4 Таблица данных по пп. 2.1.1-2.1.2 по отдельным частям выборки, содержащим по N/10 значений:

Табл.1

N	1,931	1,9765	2,534	9,2347	3,0389	-1,148	259,39	-0,040909	3,0416
N/10	2.0508	1.8638	2.2202	9.1819	3.0302	6.1684	239.21	0.2217	2.8373
N/10	1.5829	1.8409	0.36189	10.511	3.2421	-10.833	335.99	-0.31787	3.041
N/10	1.9199	1.866	0.8799	8.189	2.8616	-0.32405	213.04	-0.013828	3.1768
N/10	2.6783	2.7009	4.1048	9.3634	3.06	-1.3801	279.03	-0.048167	3.1826
N/10	2.0856	2.0155	2.7214	9.6848	3.112	4.9872	274.56	0.16547	2.9272
N/10	1.8823	1.9611	0.37956	8.0636	2.8397	-7.3357	205.29	0.32036	3.1572
N/10	1.7385	2.1953	1.2788	10.475	3.2365	-4.1382	283.05	-0.12206	2.5795
N/10	1.6587	1.5955	3.2253	9.0173	3.0029	7.7992	274.1	0.28803	3.3709
N/10	1.6917	1.5572	0.70022	8.375	2.894	-5.7703	188.24	-0.23808	2.6837
N/10	2.0218	2.0209	2.0949	8.5887	2.9306	-0.24758	231.51	-0.009836	3.1385

Оценка первого начального момента

Оценка выборочной медианы

Оценка середины размаха

Оценка второго центрального момента

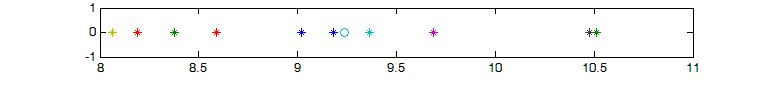
Оценка среднеквадратичного отклонения

Оценка третьего центрально момента

Оценка четвертого центрального момента

Оценка асимметрии

Оценка эксцесса

○ – оценки для n=N,          * – оценки для n=N/10

2.2. Интервальные оценки с доверительной вероятностью Q=0.8.

Для первого центрального момента по полной выборке:

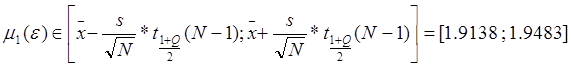
Для второго центрального момента по полной выборке:

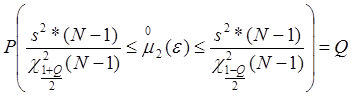
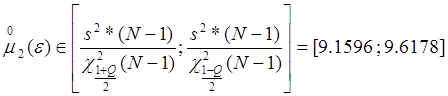
Интервальные оценки с доверительной вероятностью Q=0.8 по отдельным частям выборки n=N/10 для первого и второго центральных моментов.

Табл.2 Интервальные оценки с доверительной вероятностью Q=0.8

	первого начального момента			второго центрального момента
2.0508	2.0337	2.068	9.1819	9.1072	9.5627
1.5829	1.5645	1.6012	10.511	10.426	10.947
1.9199	1.9037	1.9361	8.189	8.1224	8.5287
2.6783	2.6609	2.6956	9.3634	9.2872	9.7517
2.0856	2.0679	2.1032	9.6848	9.6061	10.087
1.8823	1.8662	1.8984	8.0636	7.998	8.3981
1.7385	1.7202	1.7569	10.475	10.39	10.91
1.6587	1.6417	1.6757	9.0173	8.944	9.3914
1.6917	1.6753	1.7081	8.375	8.3068	8.7223
2.0218	2.0052	2.0384	8.5887	8.5188	8.9449

Для первого центрального момента.

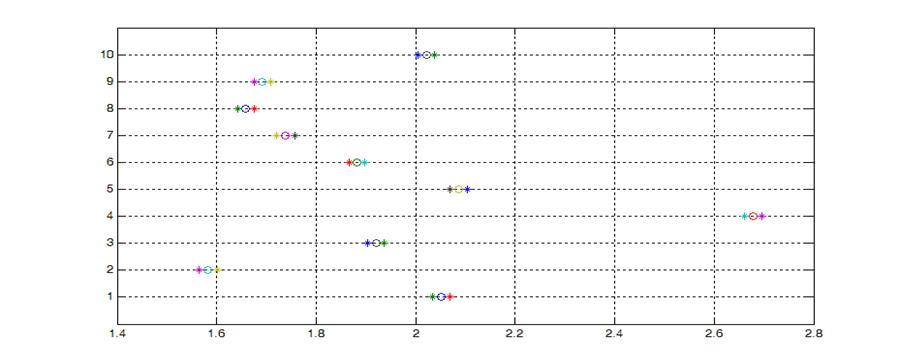
Для второго центрального момента.

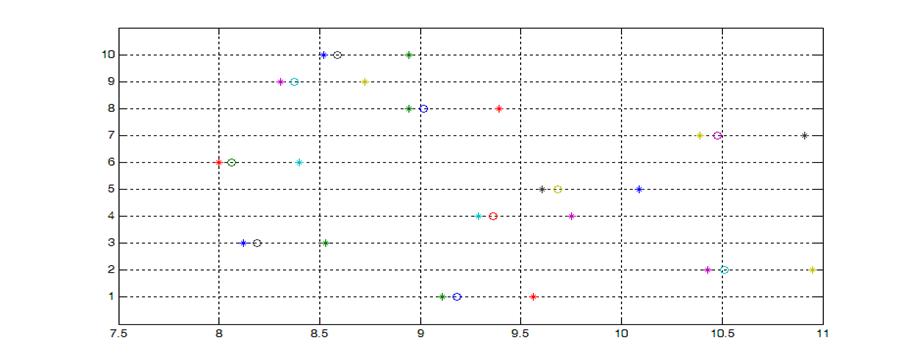
* - границы промежутков      ○ – значения моментов

Интервальные оценки с доверительной вероятностью Q=0.8 интерквантильного промежутка J для P=0.95 по всей выборке с помощью непараметрических толерантных пределов, симметричных и несимметричных относительно среднего арифметического:

J_p=[ 3.3169 ; 6.9448] (элементы отсортированной выборки, где k находится из условия )

k=90 , N-k=1910;

Интервальные оценки с доверительной вероятностью Q=0.8 интерквантильного промежутка J для P=0.95 по частичным выборкам с помощью параметрических толерантных пределов, считая закон распределения генеральной совокупности нормальным.

,  k - толерантный множитель

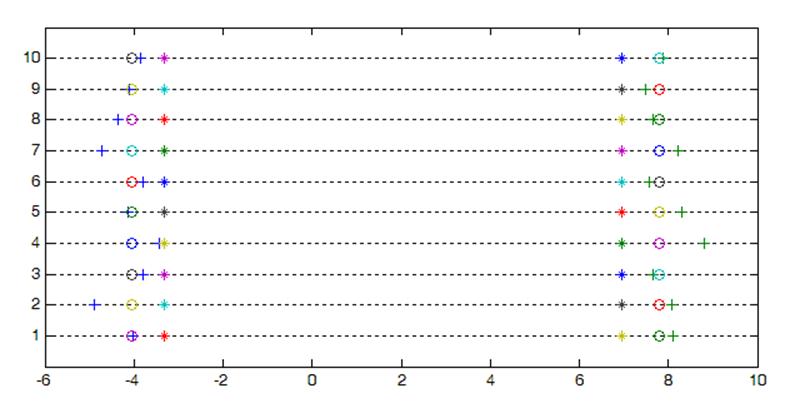
*  - Jр по всей выборке с помощью непараметрических толерантных пределов

○  - Jp для точечной оценки

+  - Jp по частичным выборкам с помощью параметрических толерантных пределов.

3. Идентифицировать закон распределения и выбрать подходящий методом проб, определяя параметры закона (если моменты параметрами не являются) и проверяя для КАЖДОЙ пробы гипотезу о соответствии предполагаемого закона распределения экспериментальным данным с помощью ТРЕХ критериев:

"хи-квадрат",     Колмогорова-Смирнова,     "омега-квадрат".

Согласно полученному графику и гистограмме, можно выдвинуть гипотезу, что выборка  – “нормальное распределение”. Кривая описывается уравнением:

Проверим гипотезу с помощью функции dfittool в MatLab, параметры посчитанные для нормального распределения совпадают с посчитанными вручную.

σ= 3.0389; μ= 1.9765

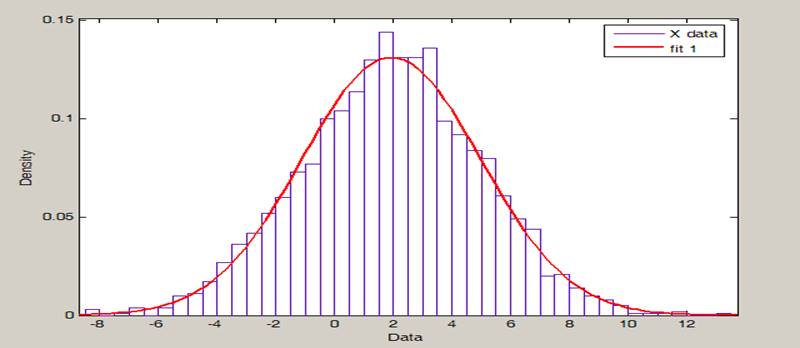
a)  Проверка гипотезы с помощью критерия «хи-квадрат»:

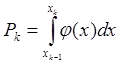 - вероятность попадания значения в интервал.

Статистика критерия  = 50.944007

Критическое значение критерия  = 59.303512, α=0.05;

50.944007 < 59.303512

Выборочные данные не противоречат гипотезе.

b)  Проверка гипотезы с помощью критерия Колмогорова-Смирнова: