Генеральная совокупность с неизвестным законом распределения. Выборочная функция распределения, страница 2

интервальная оценка второго центрального момента по полной выборке:

 

[2,0006; 2,1006]

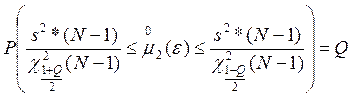
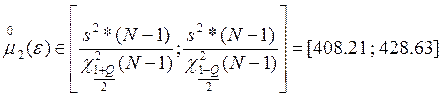
интервальные оценки отдельно по частям:

интервальная оценка первого начального момента			интервальная оценка второго центрального момента
4,0124	4,0276	4,02	1,775	1,8638	1,7896
4,0668	4,0832	4,075	2,0625	2,1656	2,0794
3,9068	3,9232	3,915	2,0708	2,1744	2,0878
4,0866	4,1034	4,095	2,1781	2,2871	2,1960
4,027	4,043	4,035	1,9776	2,0765	1,9938
4,0023	4,0177	4,01	1,8249	1,9162	1,8399
3,7768	3,7932	3,785	2,0916	2,1962	2,1088
4,0676	4,0824	4,075	1,7054	1,7907	1,7194
4,0219	4,0381	4,03	2,0324	2,1341	2,0491
4,0015	4,0185	4,01	2,2118	2,3224	2,2299

                

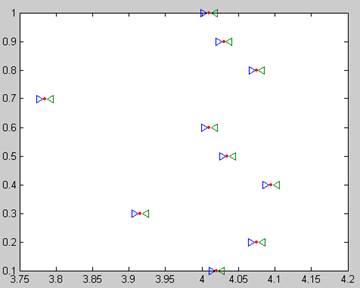
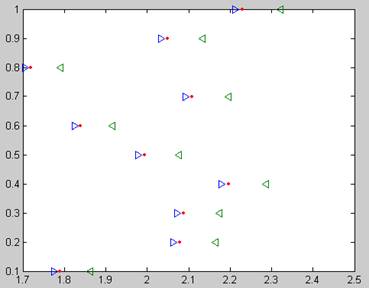
  Рис.3 Интервальная оценка первого начального момента                 Рис.4 Интервальная оценка второго центрального момента

·  интерквантильного промежутка J для P=0.95:

o  по всей выборке с помощью непараметрических толерантных пределов:

k находится из условия:  

(k=90 и N-k=1910 элементы отсортированной выборки)

J_p=[2; 6]

o  по частичным выборкам с помощью параметрических толерантных пределов, считая закон распределения генеральной совокупности нормальным:

k- толерантный множитель

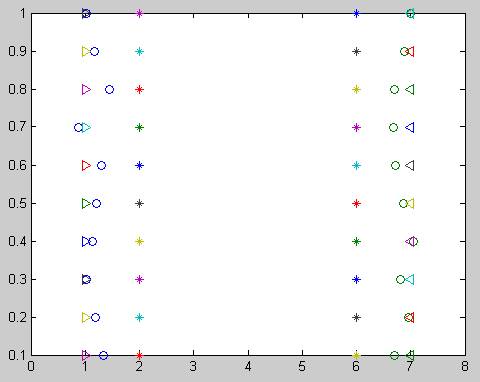
Рис.5:

* - J_р по всей выборке с помощью непараметрических толерантных пределов о   -   J_p для точечной оценки

> < - J_p по частичным выборкам с помощью параметрических толерантных пределов

3. Идентификация закона распределения по различным критериям

Гипотеза 1: выборочные значения извлечены из биномиального распределения: F=binocdf(x,2000,pi);

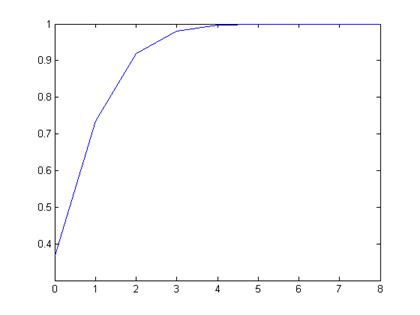Проверка гипотезы:

·   проверка гипотезы о соответствии плотности распределения выборочным данным по критерию Колмогорова-Смирнова:

статистика критерия = 0.88374

критическое значение критерия = 0.51961

0.88374 > 0.51961

Гипотеза не была подтверждена.

·   проверка гипотезы о соответствии плотности распределения выборочным данным по критерию омега-квадрат Мизеса:

статистика критерия = 0.00016667

критическое значение критерия при уровне значимости 0.05 = 0.4614 

0.00016667 < 0.4614

Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с биномиальной плотностью распределения.

·    проверка гипотезы о соответствии плотности распределения выборочным данным по критерию χ²:

статистика критерия = 600.79

критическое значение критерия = 12.592

600.79 > 12.592, Гипотеза не была подтверждена.

Гипотеза 2: выборочные значения извлечены из геометрического распределения: F = geocdf(x, pi);

Проверка гипотезы:

 

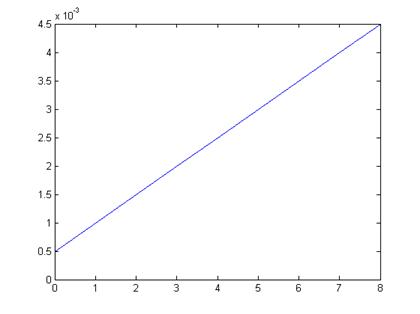
·    проверка гипотезы о соответствии плотности распределения выборочным данным по критерию Колмогорова-Смирнова:

статистика критерия = 0.99551

критическое значение критерия = 0.51961

0.99551 > 0.51961

Гипотеза не была подтверждена.

·    проверка гипотезы о соответствии плотности распределения выборочным данным по критерию омега-квадрат Мизеса:

статистика критерия = 0.00016667

критическое значение критерия при уровне значимости 0.05 = 0.4614 

0.00016667 < 0.4614

Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с биномиальной плотностью распределения.

·  проверка гипотезы о соответствии плотности распределения выборочным данным по критерию χ²:

статистика критерия = 4902.5

критическое значение критерия = 12.592

4902.5 > 12.592

Гипотеза не была подтверждена.

Гипотеза 3: выборочные значения извлечены из гипергеометрического распределения: F = hygepdf(x,400,40,100);

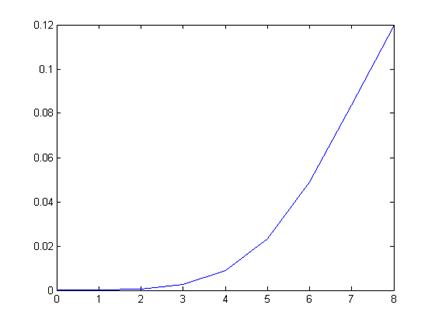Проверка гипотезы: