Генеральная совокупность с неизвестным законом распределения. Выборочная функция распределения, страница 3

·  проверка гипотезы о соответствии плотности распределения    выборочным    данным  по  критерию

Колмогорова-Смирнова:

статистика критерия = 0.2131

критическое значение критерия = 0.51961

0.3965 < 0.51961

Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с плотностью гипергеометрического распределения.

·  проверка гипотезы о соответствии плотности распределения   выборочным   данным   по   критерию омега-квадрат Мизеса:

статистика критерия = 0.00016667

критическое значение критерия при уровне значимости 0.05 = 0.4614

0.00016667 < 0.4614

Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с гипергеометрической плотностью распределения.

·  проверка гипотезы о соответствии плотности распределения выборочным данным по критерию χ²:

статистика критерия = -1.7452e+003

критическое значение критерия = 12.592

-1.7452e+003 < 12.592

Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с плотностью гипергеометрического распределения.

Гипотеза 4: выборочные значения извлечены из отрицательного биномиального распределения:

F = nbincdf(x,2001,pi);

Проверка гипотезы:

·  проверка гипотезы о соответствии плотности распределения выборочным данным по критерию Колмогорова-Смирнова:

статистика критерия = 1

критическое значение критерия = 0.51961

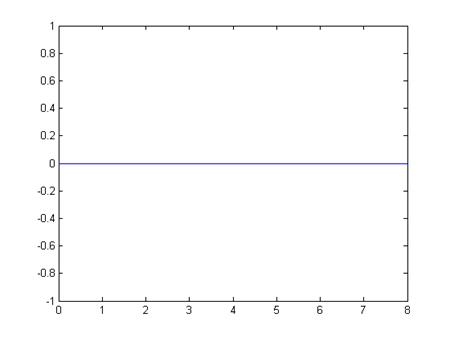1 > 0.51961, Гипотеза не была подтверждена.

·    проверка гипотезы о соответствии плотности распределения выборочным данным по критерию омега-квадрат Мизеса:

статистика критерия = 0.00016667

критическое значение критерия при уровне значимости 0.05 = 0.4614

0.00016667 < 0.4614

Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с отрицательной биномиальной плотностью распределения.

·  проверка гипотезы о соответствии плотности распределения выборочным данным по критерию χ²:

статистика критерия = Inf

критическое значение критерия = 12.592

Гипотеза не была подтверждена.

Гипотеза 5: выборочные значения извлечены из распределения Пуассона: F = poisscdf(x,4);

Проверка гипотезы:

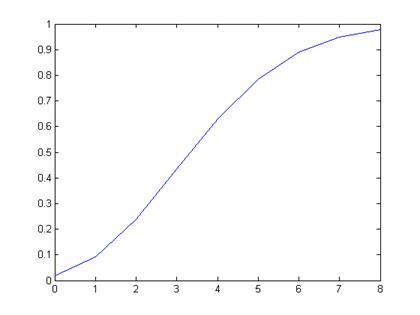
·  проверка гипотезы о соответствии плотности распределения выборочным данным по критерию Колмогорова-Смирнова:

статистика критерия = 0.28997

критическое значение критерия = 0.51961

0.28997 < 0.51961

Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с плотностью распределения Пуассона.

·  проверка гипотезы о соответствии плотности распределения выборочным данным по критерию омега-квадрат Мизеса:

статистика критерия = 0.00016667

критическое значение критерия при уровне значимости 0.05 = 0.4614

0.00016667 < 0.4614

Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с плотностью распределения Пуассона.

·  проверка гипотезы о соответствии плотности распределения выборочным данным по критерию χ²:

статистика критерия = 38.929

критическое значение критерия = 12.592

38.929 > 12.592

Гипотеза не была подтверждена.

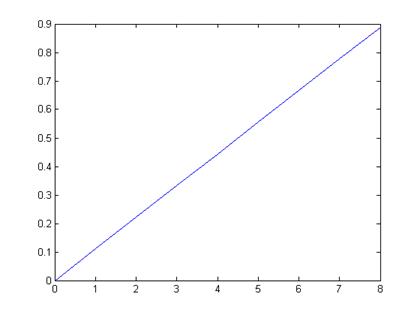Гипотеза 6: выборочные значения извлечены из равномерного распределения: F = unidcdf(x,9);

Проверка гипотезы:

·  проверка гипотезы о соответствии плотности распределения выборочным данным по критерию Колмогорова-Смирнова:

статистика критерия = 0.29794

критическое значение критерия = 0.51961

0.29794 < 0.51961

Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с плотностью распределения Пуассона.

·  проверка гипотезы о соответствии плотности распределения выборочным данным по критерию омега-квадрат Мизеса:

статистика критерия = 0.00016667

критическое значение критерия при уровне значимости 0.05 = 0.4614

0.00016667 < 0.4614

Выборочные данные не противоречат гипотезе о том, что они извлечены из генеральной совокупности с равномерной плотностью распределения.

·  проверка гипотезы о соответствии плотности распределения выборочным данным по критерию χ²:

статистика критерия = 102.91

критическое значение критерия = 12.592

102.91 > 12.592

Гипотеза не была подтверждена.

Вывод: проанализировав различные законы распределения, я пришла к выводу, что наиболее подходящим является гипергеомерическое распределение.