Санкт-Петербургский государственный технический университет Факультет Технической Кибернетики
Кафедра Компьютерных Систем и Программных Технологий
КУРСОВОЙ ПРОЕКТ
Дисциплина: Технические средства автоматики и управления
Выполнил студент гр. 4081/1
Руководитель, к.т.н., доцент
"___ "_________ 2010 г.
Санкт-Петербург 2010
1. Задание
Структурная схема исследуемой САУ представлена на рис. 1.1.

Рис. 1.1. Структурная схема исследуемой САУ.
Wн(x) – передаточная нелинейного элемента типа зазор, люфт. Его характеристика приведена на рисунке 1.2.
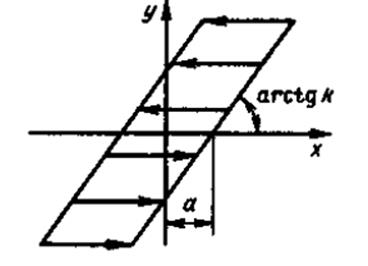
Рис. 1.2. Характеристика нелинейного элемента. a = 1, k = 1.
Передаточные функции объекта управления и регулирующего звена приведены ниже.
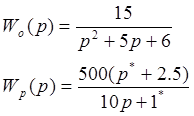
Звёздочкой отмечены изменяемые параметры.
2. Определение устойчивости системы
а) Устойчивость разомкнутой системы.
Передаточная функция разомкнутой системы:
![]()
Корни характеристического многочлена лежат в левой
полуплоскости, значит, система устойчива. ![]()
б) Устойчивость замкнутой системы.
Передаточная функция замкнутой системы:
![]()
Вещественные части корней характеристического полинома лежат
в левой комплексной полуплоскости(<0), значит, система устойчива. ![]()
3. Построение области устойчивости замкнутой системы в плоскости изменяемых параметров
Для определения устойчивости системы воспользуемся критерием Гурвица. Раскроем скобки в характеристическом полиноме замкнутой системы:
![]()
По критерию Гурвица, для того чтобы система была устойчива, должно выполняться условие: Произведение средних коэффициентов должно быть больше произведения крайних. Поэтому можно записать:
![]()
Здесь х и у – изменяемые параметры системы.
Для построения этой плоскости графически воспользуемся программой dcomв matlab, приведенной в следующем листинге:
|
function [] = dcom( q_string, range_x, range_y ) % DCOM (сокр. D-decomposition). Построение D-разбиения в % пространстве двух варьируемых параметров х,у системы % с характеристическим уравнением, заданным в строке q_string % q_string - символьная запись знаменателя передаточной функции % с двумя варьируемыми параметрами х и у % range_x - массив абсцисс в формате [минимум:шаг:максимум] % range_y - массив ординат в формате [минимум: шаг: максимум] % Пример вызова: % q_string - '[1, х-1.2, у-0.8*х+0.48, 0.16*х-0.4*у+0.936]'; % range_x = [0:0.1:10]; % range_y = [0:0.1:10]; % dcom( q_string, range_x, range_y ); n = length ( range_x ); m = length ( range_y ); P = zeros ( m, n ); % Матрица, соответствующая плоскости % двух параметров, ненулевые значения % элементов которой говорят % о неустойчивости системы % Сканирование и проверка на устойчивость в плоскости (х,у) for i = 1:n for j = 1:m x = range_x( i ); % Текущая абсцисса y = range_y( j ); % Текущая ордината q = eval( q_string ); % Значение знаменателя в текущей точке P ( j, i ) = rr( q ); % Количество правых полюсов % в данной точке end end % Построение окна F = figure; A = axes( 'Parent', F, ... 'Position', [0.1 0.1 0.85 0.85], ... 'Units', 'normalized', ... 'NextPlot', 'add', ... 'ButtonDownFcn', 'dcom_action;', ... 'Tag', 'Axes', ... 'UserData', q_string ); % Построение графика D-разбиения contour ( range_x, range_y, P ); xlabel( 'x' ), ylabel( 'y' ); title( 'D-разбиение' ); grid on; function [] = dcom_action() % DCOM_ACTION - функция обработки нажатия левой кнопки мыши % в активном окне h = gcbo; % Объект, для которого вызван обработчик cp = get( h, 'CurrentPoint' ); % Указываемая мышью точка х = ср( 1, 1 ); у = ср( 1, 2 ) ; q_string = get( h, 'UserData' ); % Исследуемый полином n = rr ( eval ( q_string ) ); % Количество правых полюсов s = sprintf( ' D(%i)', n ); % Подготовка строки text ( x, y, s )'; % Вывод строки на график plot ( x, y, '.' ); % Вывод текущей точки на гра function n = rr( q ) % RR (RightRoots) вычисляет n - количество правых полюсов I полинома q p = roots( q ); k= find( real ( p ) >= 0 ); % Индексы полюсов, расположенных % в правой полуплоскости if( isempty( k ) == 0 ) % Имеется length(к) правых полюсов n = length( k ); else n = 0; % Правые полюса отсутствуют end |
Для построения D-разбиения выполним следующую команду:
dcom('[10, 51, 65+7500*x, 18750+6*y]', -0.4:0.01:1, -5000:100:5000)
Результат D-разбиения представлен на рисунке.
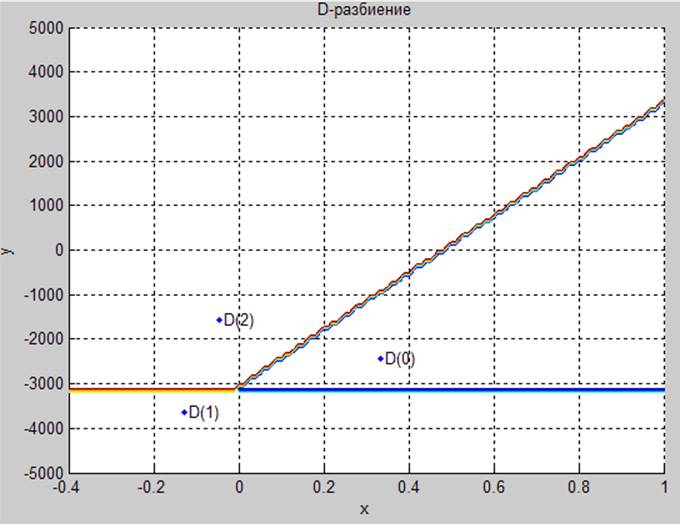
Рис 3.1. Области устойчивости в плоскости двух параметров системы
Система устойчива только в области параметров D(0).
4. Подбор корректирующего звена для установки переходного процесса с заданными параметрами
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.