Исследование системы автоматического управления. Построение границ областей устойчивости в плоскости заданных параметров

1).  Задание на курсовой проект ..........................................................................

2).  Исследование системы автоматического управления ………………….

2.1). Исследование устойчивости замкнутой системы …………………………

2.2). Построение границ областей устойчивости в плоскости заданных параметров…………………………………………………...........................

2.3). Построение линий равной степени устойчивости в плоскости заданных  параметров.                             

2.4). Построение переходного процесса для оптимальных значений                   параметров и определение показателей качества переходного процесса...

2.5). Построение фазового портрета нелинейной системы…………………….

2.6). Исследование автоколебаний при включении на входе регулятора                 нелинейного звена…………………………………………………………...

3).  Выводы ……………………………………………………………………….

4).  Список используемой литературы ……………………………………….

1.  Задание на курсовой проект

1.1. Описание исследуемой САУ

На  рисунке 1.1 представлена структурная схема исследуемой системы автоматического управления.

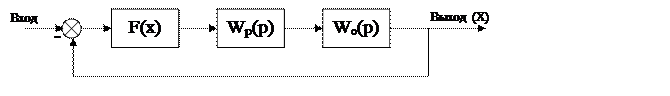Рис. 1.1. Структурная схема исследуемой САУ

F(x) – передаточная функция нелинейного элемента (трехпозиционного реле), характеристика которого представлена на рисунке 1.2, где b = 0,2; c = 1.

 - передаточная функция устройства управления;

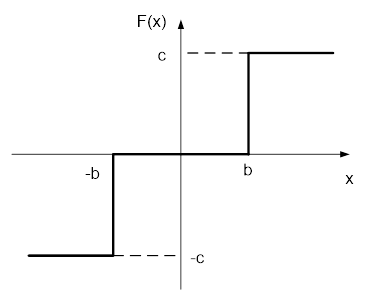
Рис.1.2  Характеристика нелинейного элемента

Заданные параметры САУ:

Объекта управления: К₀ =2; Т₀₁ =0,12с; Т₀₂ =0,4с.

Устройства управления:T =0,05с;=20.

Нелинейного звена: b =0,2;  c =1.

1.2.    Этапы исследования САУ        

1.  Исследовать устойчивость замкнутой и разомкнутой линейной системы.

2.  Построить границы областей устойчивости в плоскости параметров, отмеченных *.

3.  Построить линии равной степени устойчивости в плоскости тех же параметров.

4.  Построить переходный процесс для единичного ступенчатого воздействия на входе при нулевых начальных условиях для оптимальных значений параметров (по п.3). Определить показатели качества переходного процесса.

5.  Построить фазовый портрет нелинейной системы второго порядка, считая регулятор безынерционным звеном и полагая W_р(p)=1. Сделать выводы о характере процессов в системе.

По фазовым траекториям построить примерный вид переходных процессов для  характерных начальных условий.

6.  Промоделировать нелинейную систему 2-го порядка в Simulink. Сравнить фазовые портреты, полученные расчетным способом с результатами моделирования.

Ввести обратную связь по скорости и исследовать ее влияние на процессы в системе.

7.  Исследовать автоколебания при включении в систему на входе регулятора нелинейного звена. Исследовать условия возникновения автоколебаний (найти К_гр. или Т_гр.).

Построить зависимости амплитуды и частоты автоколебаний от К или Т.

2.  Исследование системы автоматического управления

2.1.  Исследование устойчивости САУ

2.1.1.  Исследование устойчивости разомкнутой системы

Передаточная функция разомкнутой системы:

Подставим значения параметров САУ и получим:    

Характеристический полином разомкнутой системы:

Коэффициенты характеристического полинома разомкнутой системы:

Все коэффициенты характеристического полинома () не отрицательны.

Вычислим определитель Гурвица D_n-1:

Определитель Гурвица положителен, поэтому с учетом равенства нулю одного из коэффициентов  характеристического полинома, можно сделать вывод о том, что разомкнутая система находится на границе устойчивости.

2.1.2.  Исследование устойчивости замкнутой системы

Передаточная функция замкнутой системы:

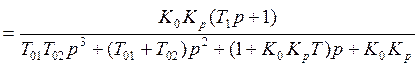
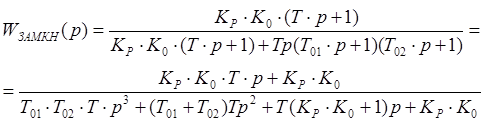
Подставим значения параметров САУ и получим:    

Характеристический полином замкнутой системы:

Коэффициенты характеристического полинома замкнутой системы:

Все коэффициенты характеристического полинома () положительны.

Вычислим определитель Гурвица D_n-1:

Определитель Гурвица отрицателен, поэтому можно сделать вывод о том, что при  исходных значениях параметров замкнутая система неустойчива.

2.2.  Построение границ областей устойчивости в плоскости заданных параметров K_Р и Т

Апериодическая граница устойчивости (нулевой корень характеристического уравнения) будет в том случае, когда ; из этого равенства получаем первую границу устойчивости: .

Для нахождения колебательной границы устойчивости (пара чисто мнимых корней) воспользуемся критерием Михайлова, по которому колебательная граница устойчивости соответствует равенству: , т.е. прохождению кривой Михайлова через начало координат (здесь w – значение чисто мнимого корня, т.е. частота гармонических колебаний системы).

Преобразуем данное уравнение в систему уравнений:   

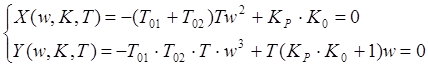    (1)

Решая данную систему уравнений, получаем следующие соотношения: