Исследование устойчивости разомкнутой и замкнутой системы. Построение фазового портрета нелинейной системы второго порядка

Линии равной степени колебательности в плоскости параметров K_p и T_p

Для более точной локализации оптимальной с точки зрения устойчивости области пределы отображения были изменены на “area = [ 0 0.0005 0.04; 0 0.01 1 ];”. Рассчитанные линии равной степени устойчивости для данного случая представлены на рис. 7.

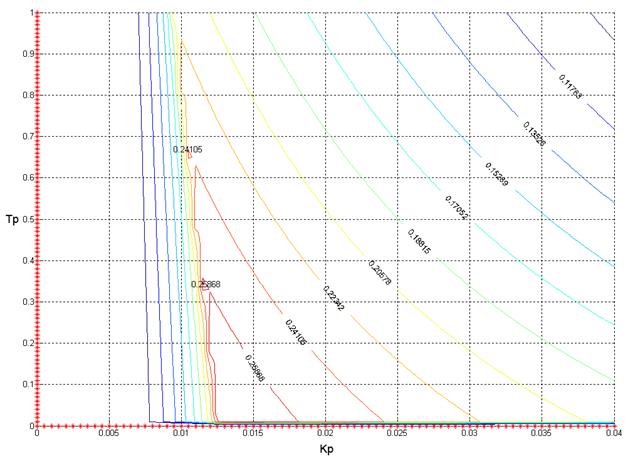
Рис. 7. Линии равной степени устойчивости в плоскости параметров K_p и T_p

при T_p=0..1, K_p=0..0,04

4. Построение переходного процесса для единичного ступенчатого воздействия на входе при нулевых начальных условиях для оптимальных значений параметров K_p и T_p. Определение показателей качества переходного процесса.

С помощью предоставляемых программой RTANALTI средств были получены переходные процессы для единичного ступенчатого воздействия на входе при нулевых начальных условиях для различных значений параметров Kp и Tp – были взяты значения как из области с оптимальными параметрами, так и вне ее.

Показатели качества переходного процесса вычислялись следующим образом:

Быстродействие: время достижения 0,95x_ст, где x_ст – установившееся значение.

Перерегулирование:

Колебательность:

Графики переходных процессов для различных наборов параметров представлены на рис. 8-12.

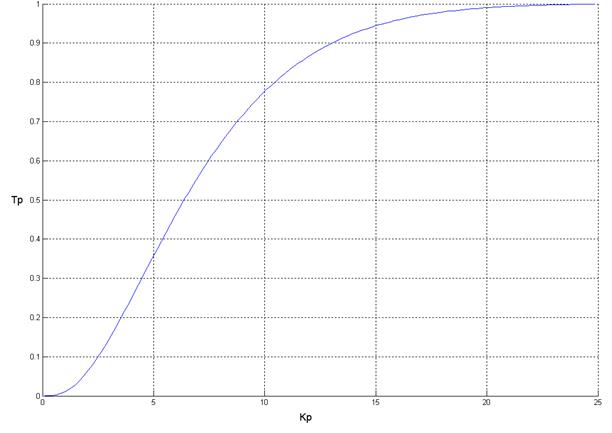
Рис. 8. Переходный процесс для единичного ступенчатого воздействия на входе при нулевых начальных условиях для Kp=0.01392, Tp=0.070242

Значение степени устойчивости: 0.268472

Значение степени колебательности: 0.407340

Быстродействие: 15 сек

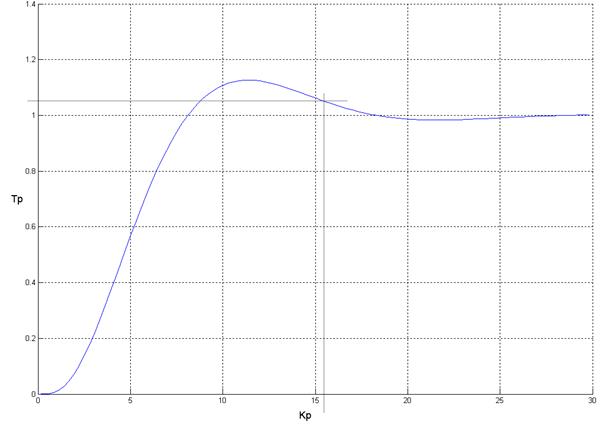
Рис. 9. Переходный процесс для единичного ступенчатого воздействия на входе при нулевых начальных условиях для Kp = 0.025038, Tp = 0.401057

Значение степени устойчивости: 0.198145

Значение степени колебательности: 1.551840

Быстродействие: 16 сек

Перерегулирование: 13%

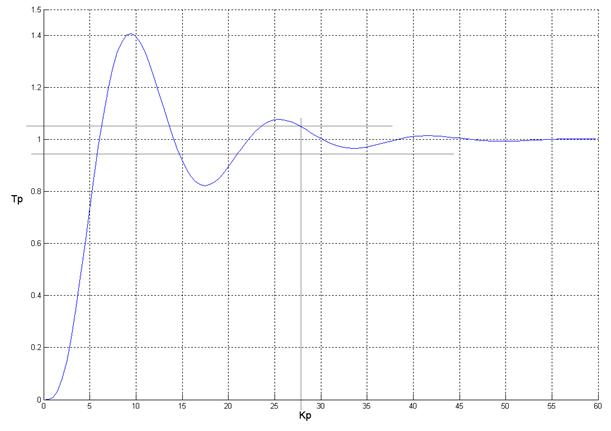
Рис. 10. Переходный процесс для единичного ступенчатого воздействия на входе при нулевых начальных условиях для Kp = 0.039110, Tp = 0.919184

Значение степени устойчивости: 0.103578

Значение степени колебательности: 3.766642

Быстродействие: 28 сек

Перерегулирование: 41%

Колебательность: 19,5%

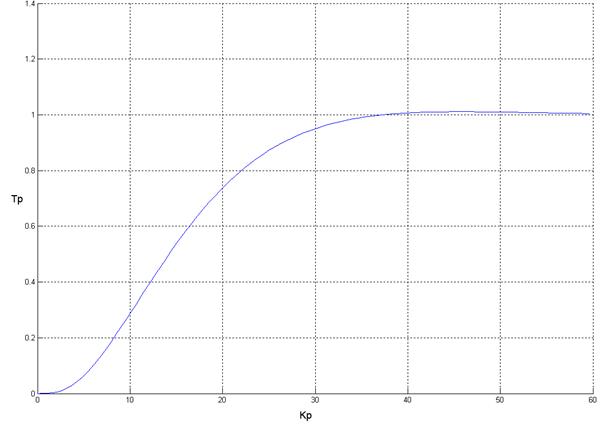
Рис. 11. Переходный процесс для единичного ступенчатого воздействия на входе при нулевых начальных условиях для Kp = 0.006623, Tp = 3.753776

Значение степени устойчивости: 0.103644

Значение степени колебательности: 0.700328

Быстродействие: 30 сек

Перерегулирование: 1%

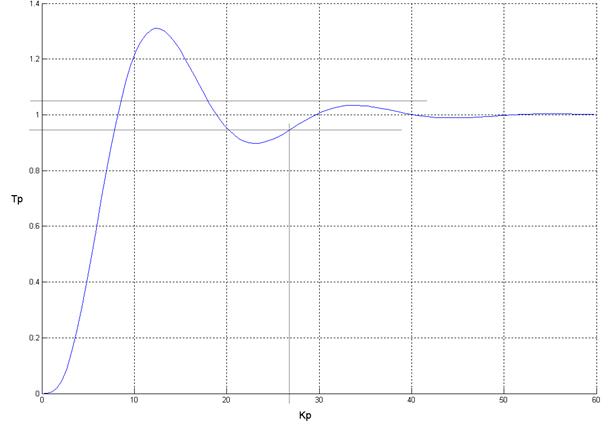
Рис. 12. Переходный процесс для единичного ступенчатого воздействия на входе при нулевых начальных условиях для Kp = 0.026819, Tp = 1.563444

Значение степени устойчивости: 0.103481

Значение степени колебательности: 2.835998

Быстродействие: 27 сек

Перерегулирование: 31%

Колебательность: 13%

5. Построение фазового портрета нелинейной системы второго порядка.

Регулятор считается безынерционным звеном, и W_р(p) полагается равным 1.

Передаточная функция линейной части системы:

Запишем в следующем виде:

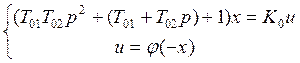
Преобразованная система:

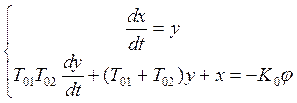
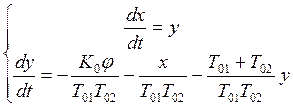
Получили ДУ, задающее фазовый портрет нелинейной системы:

Теоретический фазовый портрет нелинейной системы представлен на рис. 13, примерный вид переходного процесса, построенный на основании полученного фазового портрета, представлен на рис. 14.

Рис. 13. Теоретический фазовый портрет нелинейной системы.

Рис. 14. Примерный вид переходного процесса

6. Моделирование нелинейной системы 2-го порядка в Simulink.

Для моделирования нелинейного элемента – трехпозиционного реле, – использовалась связка из двух нелинейностей типа гистерезис. Схема элемента, реализованная в пакете Simulink, приведена на рис. 15. Результаты моделирования приведены на рис. 16.

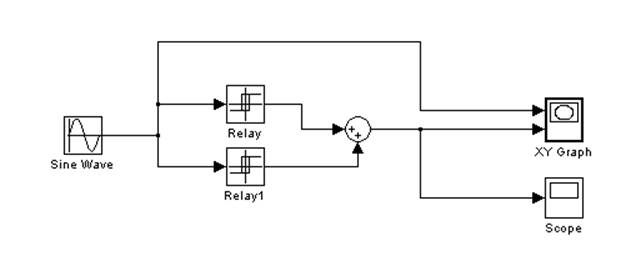
Рис. 15. Схема нелинейного элемента – трехпозиционного реле

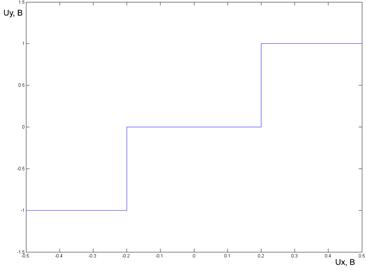
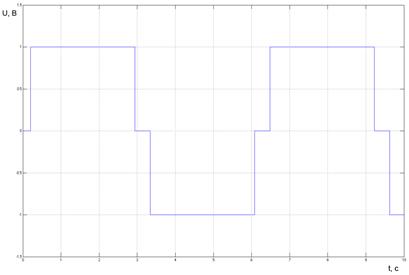
Рис. 16. Результаты моделирования работы трехпозиционного реле.

Передаточную функцию звена второго порядка  можно представить в виде:

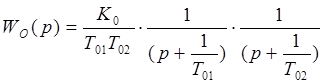
Исходя из этих соображений, система была смоделирована в пакете Simulink следующим образом:

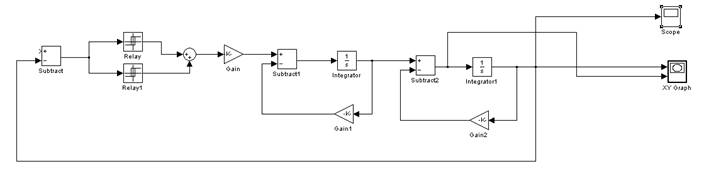
Рис. 17. Схема модели системы второго порядка

Фазовый портрет системы и переходный процесс для начального условия U=1В (в модели задаются на интеграторах) представлены на рис. 18, 19. Фазовый портрет системы и переходный процесс для начального условия U= -1В представлены на рис. 20, 21.

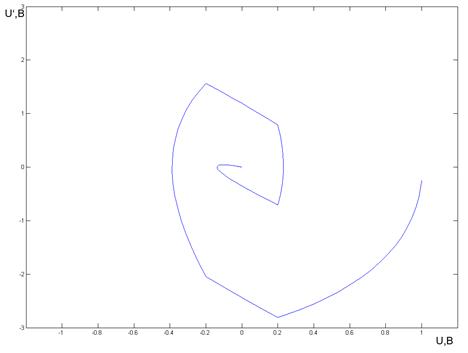
Рис. 18. Фазовый портрет системы 2 порядка при начальном условии U=1В

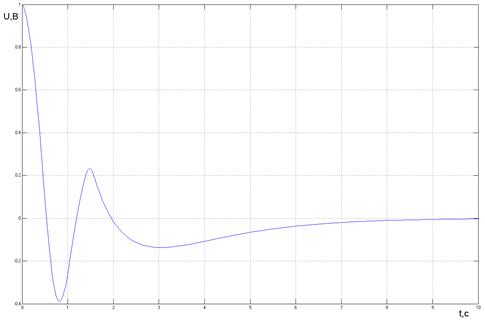
Рис. 19. Переходный процесс в системе 2 порядка при начальном условии U=1В

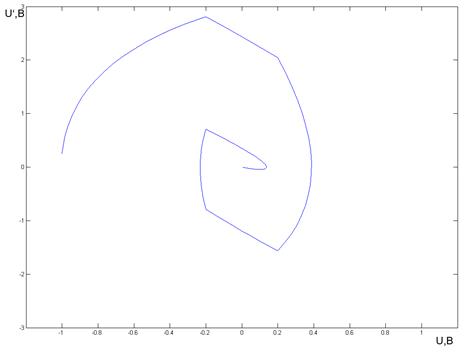
Рис. 20. Фазовый портрет системы 2 порядка при начальном условии U= -1В

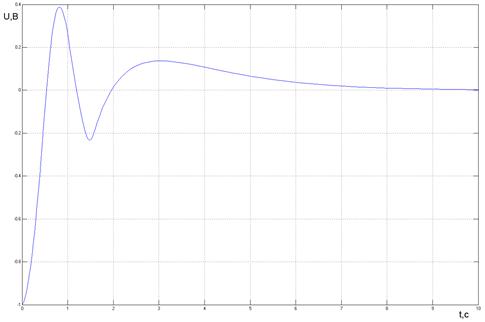
Рис. 21. Переходный процесс в системе 2 порядка при начальном условии