Санкт-Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Компьютерных Cистем и Программных Nехнологий
Отчет
о лабораторной работе №14
«Исследование динамических свойств замкнутых импульсных систем»
По дисциплине «Теория автоматического управления»
Работу выполнил студент группы 4081/1
Преподаватель:
Санкт-Петербург
2010
1. Цель работы.
Изучение методов анализа устойчивости замкнутой импульсной системы, исследование влияния изменения параметров системы и шага квантования по времени на динамические свойства системы.
Определение параметров системы с конечным временем переходного процесса.
2. Исходные данные.
1) W(p) = k/(Tp+1)
K = 6.5
T = 0.7
2) W(p) = k(Tp+1)/p2
K = 4
T = 0.75
3) W(p) = k/p(Tp+1)
K = 5
T = 0.6
3. Программа работы.
Для пунктов 1), 2) и 3) будем получать точные дискретные модели разомкнутых и замкнутых систем. По ним будет определять предельное значение коэффициента усиления и его оптимальное значение, если оно существует. Будем приводить осциллограммы выходного сигнала блока непрерывной передаточной функции и его цифрового представления с выхода АЦП для значений предельного коэффициента, 0.8 от предельного, заданного и оптимального. Используется пакет Simulink среды MatLab.
Во второй части исследования будем находить предельное значение периода квантования по времени. Будем получать переходные процессы для различных значений коэффициента передачи и периода квантования.
4. Исследуемые схемы.
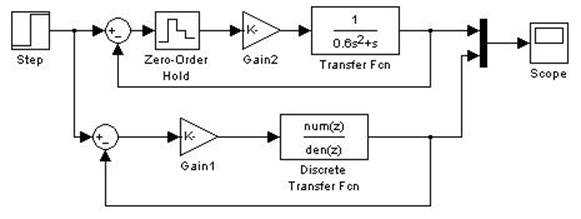
Рис.4. Схема для моделирования.
5. Выполнение работы.
5.1. Звено 1
Передаточная функция W(p)=k/(Tp+1).
W(p) = 6.5/(0.7p+1)
Исследование аналитическими методами и моделирование в Simulink.
Расчет дискретной передаточной функции разомкнутой и замкнутой системы, значений предельного и оптимального коэффициента усиления:
1. дискретная ПФ W(z) разомкнутой системы
С/Tp+1 => C(1-d)/(z-d), d = e-h/T
W(z) = 6.5(1 - e-1/7)/ (z - e-1/7)
W(z) = kb0/(a1z + a0)
b0 = 1 - e-1/7
a1 = 1
k = 6.5
a0 = - e-1/7
2. дискретная ПФ H(z) замкнутой системы
H(z) = W(z)/(1 + W(z))
H(z) = 6.5(1 - e-1/7)/(z +6.5 – 7 e-1/7)
H(z) = kb0/(a1z + a0 + kb0)
3. предельное значение k
Билинейное преобразование: z = (1+w)/(1-w)
Подставляем в знаменатель: a1((1+w)/(1-w)) + a0 + kb0
a1 (1 + w) + (a0 + kb0)(1 – w) = (a1 – a0 - kb0)w + a1 + a0 + kb0
a0’ = 0
a0’ = a1 – a0 - kb0 = 0
k = (a1 – a0)/ b0
kпред = (1 + e-1/7)/(1 - e-1/7)
kпред = 14, 0238
4. оптимальное значение H
Все коэффициенты H(z) = 0, кроме старшего
a0 = kb0 = 0
kопт = e-1/7/(1 - e-1/7)
kопт = 6,5119
Результаты моделирования с различными коэффициентами усиления и шагами дискретизации, полученные с помощью Simulink, приведены ниже.
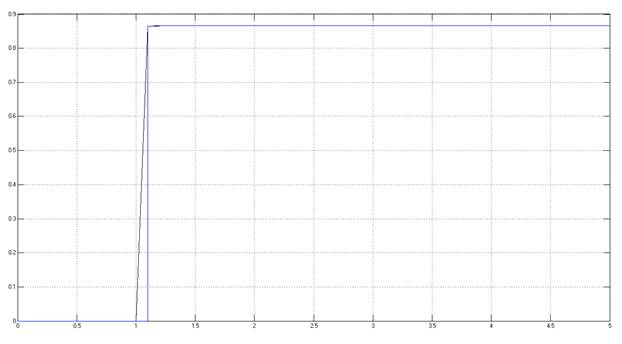
Рис.5.1.1. Осциллограмма выходных сигналов (К=6.5 (заданный), шаг=0.1с (заданный) ).
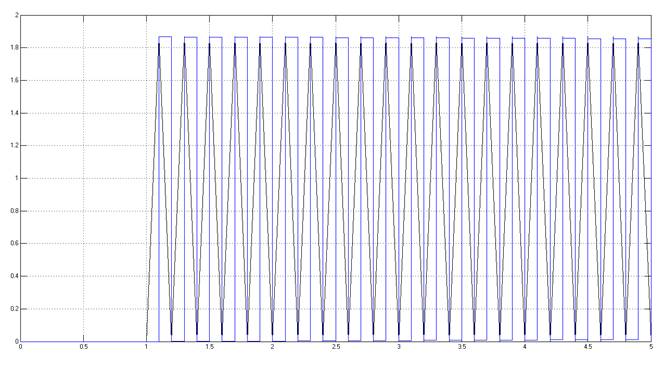
Рис.5.1.2. Осциллограмма выходных сигналов (К-предельный, шаг=0.1с (заданный) ).
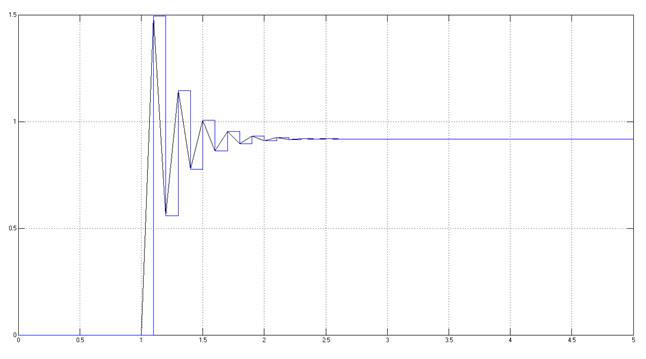
Рис.5.1.3. Осциллограмма выходных сигналов (К-0.8*предельный, шаг=0.1с (заданный) ).
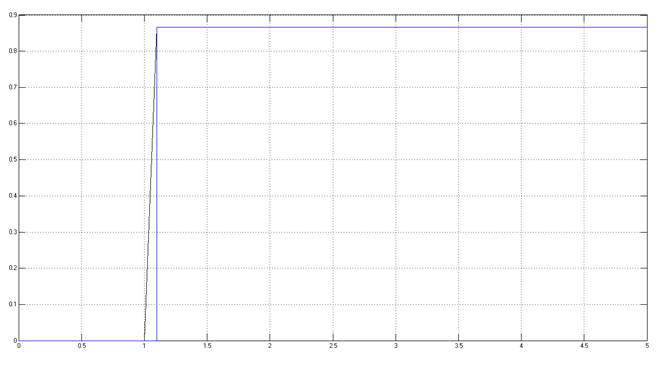
Рис.5.1.5. Осциллограмма выходных сигналов (К-оптимальный, шаг=0.1с (заданный) ).
Исследование влияния периода квантования на качество процессов и построение переходных процессов с помощью скрипта discr.
Расчет предельного значения периода квантования по времени:
Найдём из того же условия, что и предельное значение коэффициента усиления.
a0’ = 0
a1 - a0 - kb0 = 0
a0 = -d = -e-h/T
a1 = 1
k = 6.5
b0 = 1 – d = 1 -e-h/T
1 + d – k(1 – d) = 0
d = (k – 1)/(k + 1)
-e-h/T = (k – 1)/(k + 1)
h = -Tln((k - 1)/(k + 1))
k = 6.5
T = 0,7
h = 0,21708
Полученные переходные процессы для различных шагов дискретизации и коэффициентов усиления приведены ниже.
Предельный коэффициент передачи системы при шаге дискретизации 0.1 с, полученный с помощью скрипта discr, равен 14.0238.
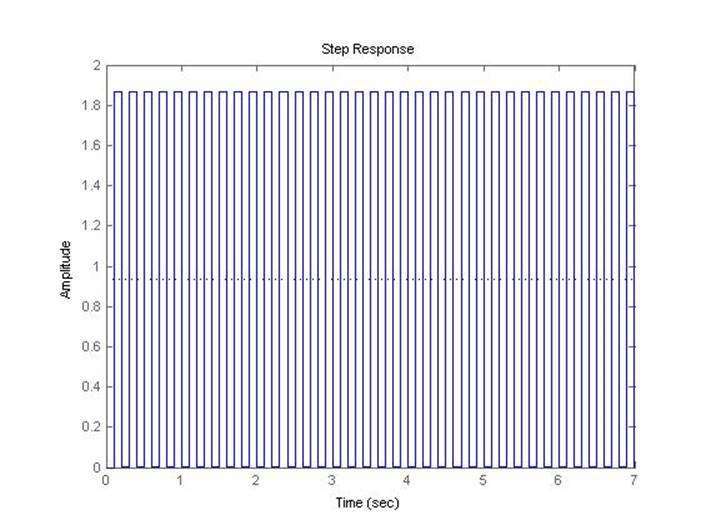
Рис.5.1.6. Осциллограмма выходного сигнала (К-предельный, шаг=0.1с).
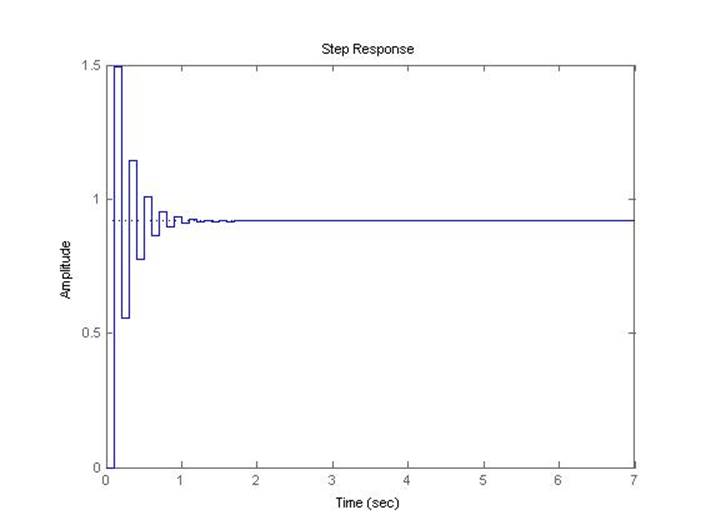
Рис.5.1.7. Осциллограмма выходного сигнала (К-0.5*предельный, шаг=0.1с).
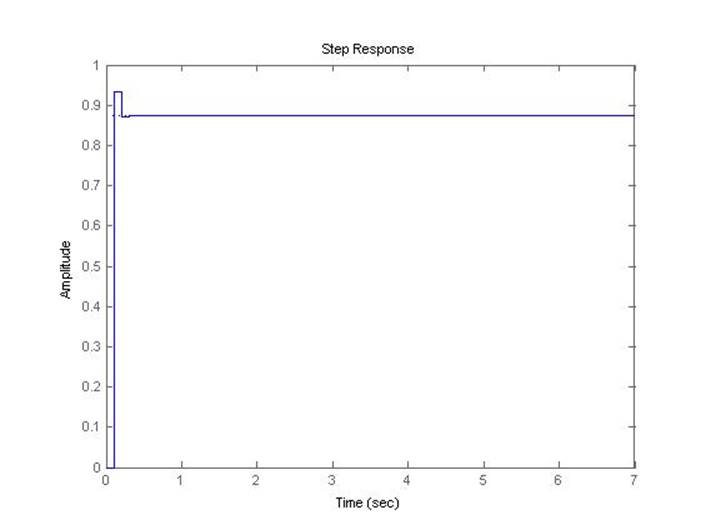
Рис.5.1.8. Осциллограмма выходного сигнала (К-0.8*предельный, шаг=0.1с).
Предельный коэффициент передачи системы при шаге дискретизации 0.5 с, полученный с помощью скрипта discr, равен 2.916.
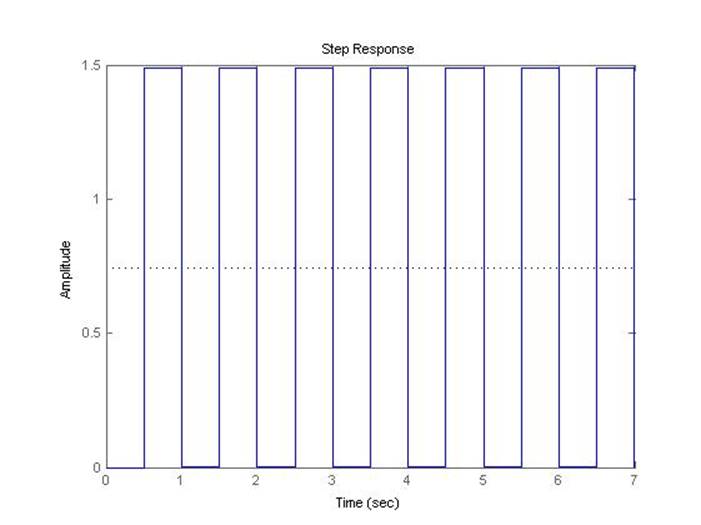
Рис.5.1.9. Осциллограмма выходного сигнала (К-предельный, шаг=0.5с).
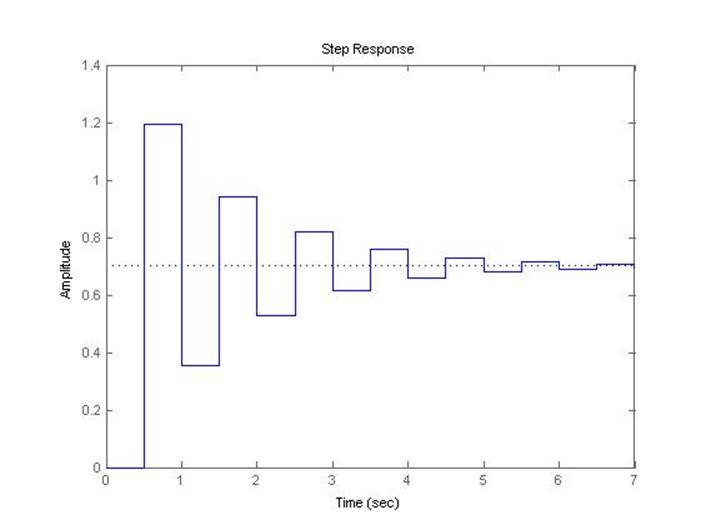
Рис.5.1.10. Осциллограмма выходного сигнала (К-0.5*предельный, шаг=0.5с).
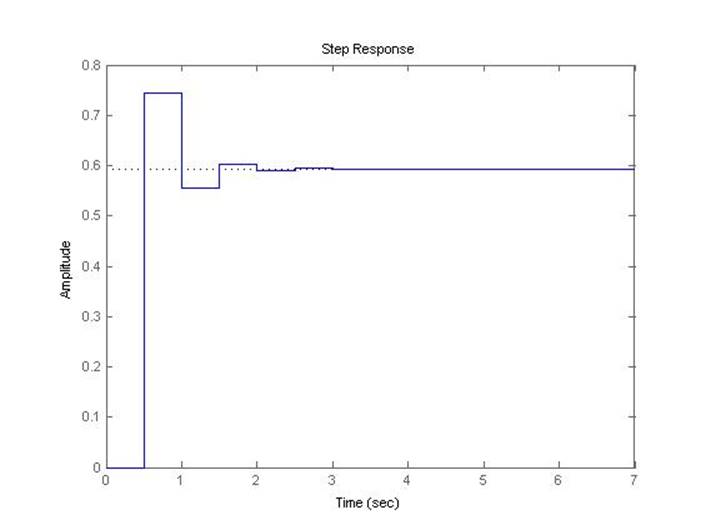
Рис.5.1.11. Осциллограмма выходного сигнала (К-0.8*предельный, шаг=0.5с).
Предельный коэффициент передачи системы при шаге дискретизации 1 с, полученный с помощью скрипта discr, равен 1.8031.
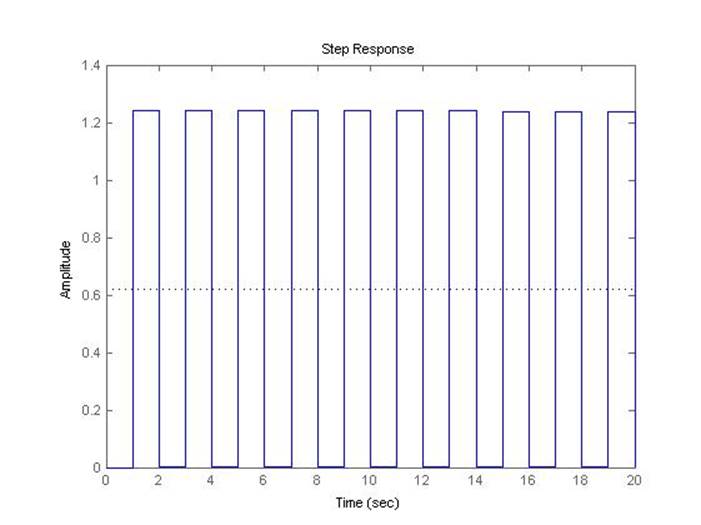
Рис.5.1.12. Осциллограмма выходного сигнала (К-предельный, шаг=1с).
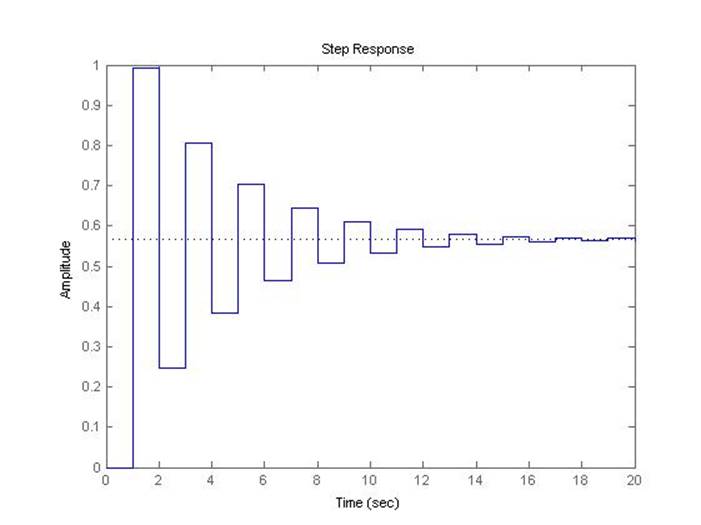
Рис.5.1.13. Осциллограмма выходного сигнала (К-0.5*предельный, шаг=1с).
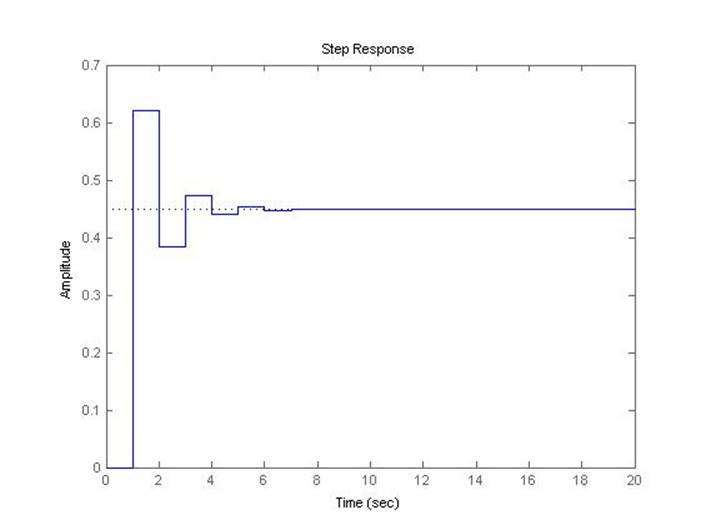
Рис.5.1.14. Осциллограмма выходного сигнала (К-0.8*предельный, шаг=1с).
5.2. Звено 2.
Заданная передаточная функция непрерывной системы.
W(p) = k(Tp+1)/p2
K = 4
T = 0.75
Дискретная передаточная функция системы с идеальным ключом и фиксатором на входе при Тдискр=0.07.
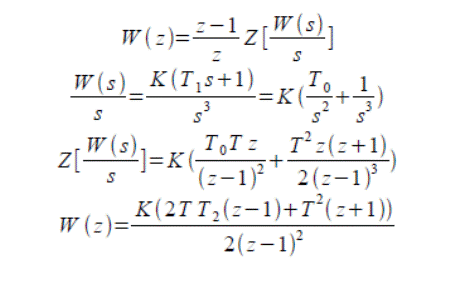
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.