Дискретную передаточную функцию разомкнутой и замкнутой системы можно рассчитать из исходной непрерывной системы используя функции пакета Control System Toolbox Matlab.
Wc = tf(4*[.75 1],[1 0 0])
T=0.07;
Wd = c2d(Wc, T);
[num_Wd,den_Wd,ts_Wd]=tfdata(Wd);
0.2198 z - 0.2002
W = ---------------------
z^2 - 1.78 z + 0.7998
H(z) – передаточная функция замкнутой системы. Рассчитывается аналогично непрерывной системе.
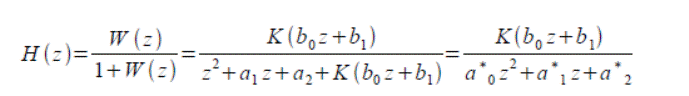
Передаточную функцию замкнутой системы можно так же рассчитать с помощью Control
System Toolbox.
Hd = feedback(Wd, 1)
[num_Hd,den_Hd,ts_Hd]=tfdata(Hd);
0.05495 z - 0.05005
W = ----------------------
z^2 - 1.945 z + 0.9499
Расчет предельного К
Сделаем замену переменных (билинейное преобразование) и применим критерий Гурвица.
Характеристическое уравнение системы:
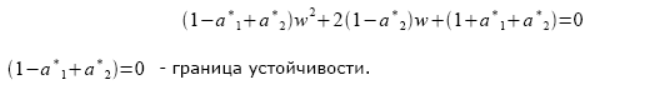
1+2-0,05495К+1-0,005005К=0
К=38,09523..
Оптимального К не существует
Моделирование системы в Simulink.
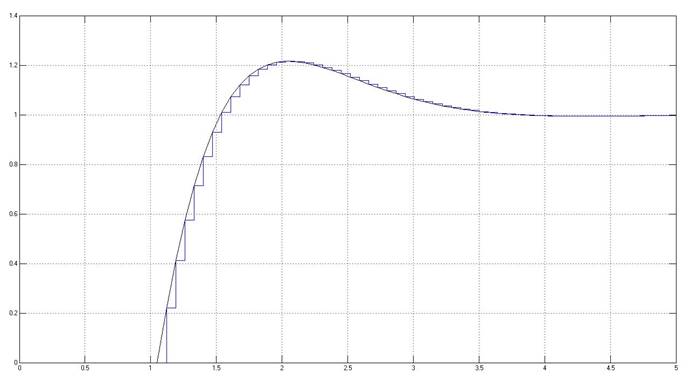
Рис.5.2.1. Осциллограмма выходных сигналов (К-4(заданный), шаг=0.07с).
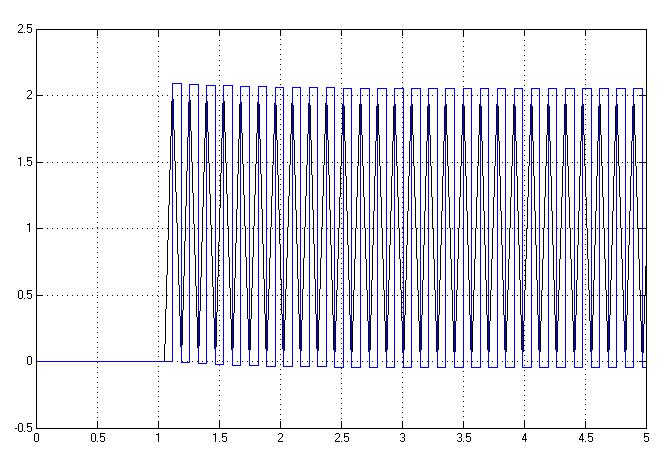
Рис.5.2.2. Осциллограмма выходных сигналов (К-предельный, шаг=0.07с).
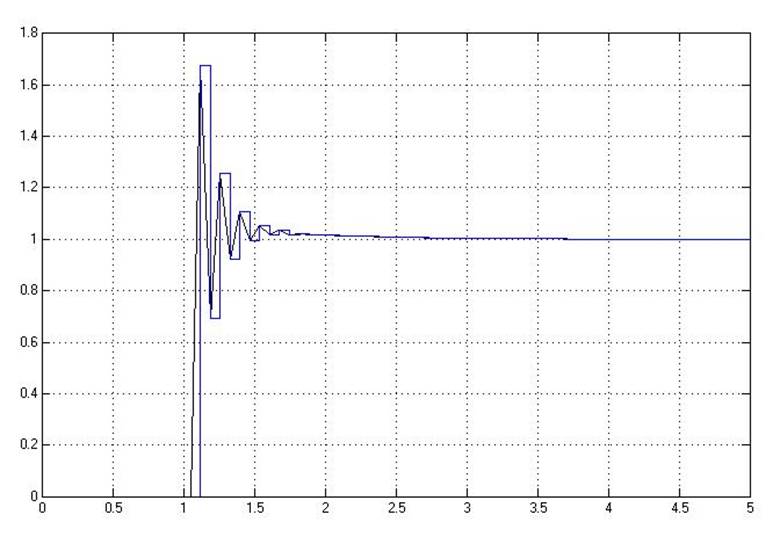
Рис.5.2.3. Осциллограмма выходных сигналов (К-предельный*0,8, шаг=0.07с).
Часть 2.
Исследование влияния периода квантования на качество процессов.
Предельное значение периода квантования найдем из того же условия, что и предельное значение коэффициента усиления.
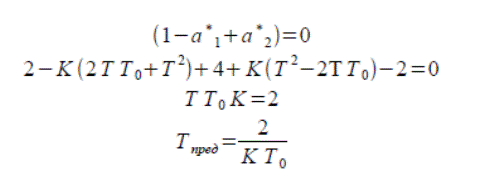
Тпред=2/3 с
Предельные коэффициенты передачи системы получены подстановкой в предыдущую формулу.
Т=0,1с Кпр=26,666..
Т=0,5с Кпр=5,3333…
Т=1с Кпр=2,6666…
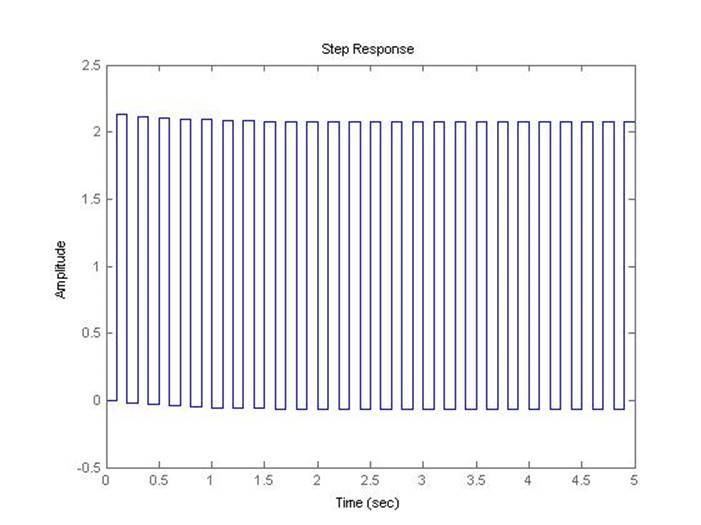
Рис.5.2.4. Осциллограмма выходного сигнала (К-предельный, шаг=0.1с).
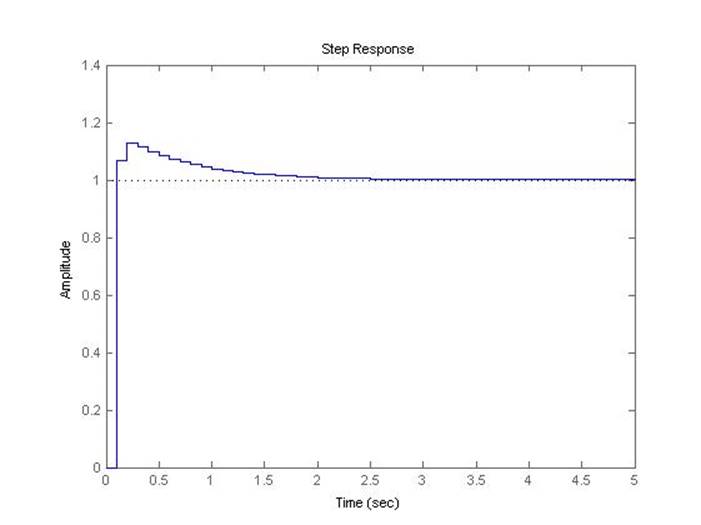
Рис.5.2.5. Осциллограмма выходного сигнала (К-0.5*предельный, шаг=0.1с).
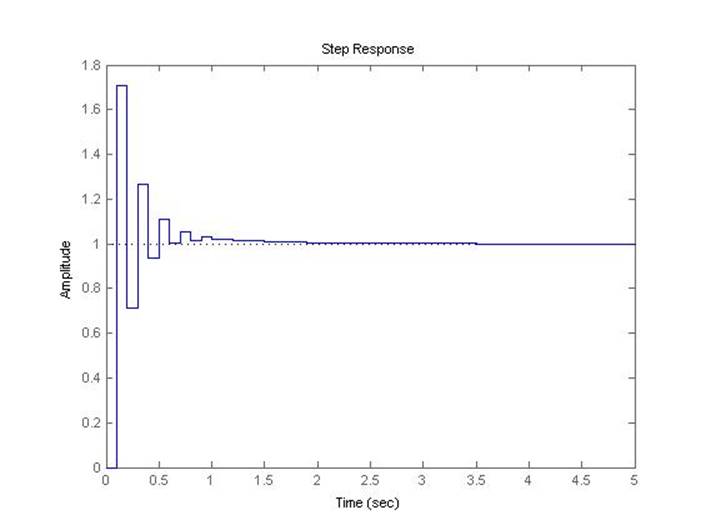
Рис.5.2.6. Осциллограмма выходного сигнала (К-0.8*предельный, шаг=0.1с).
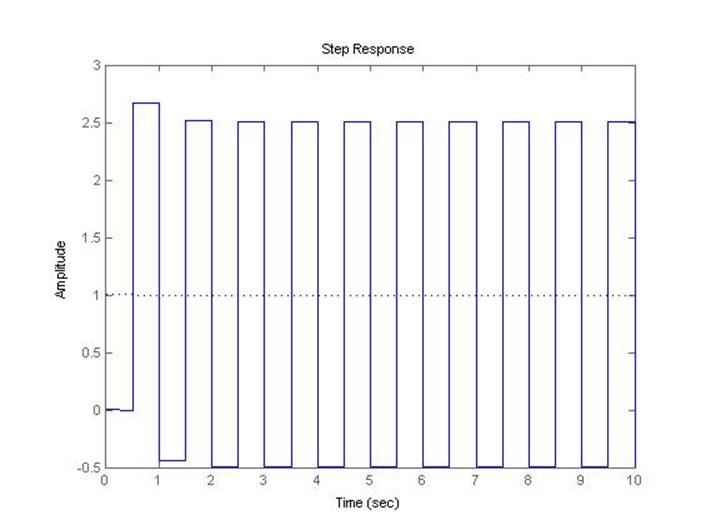
Рис.5.2.7. Осциллограмма выходного сигнала (К-предельный, шаг=0.5с).
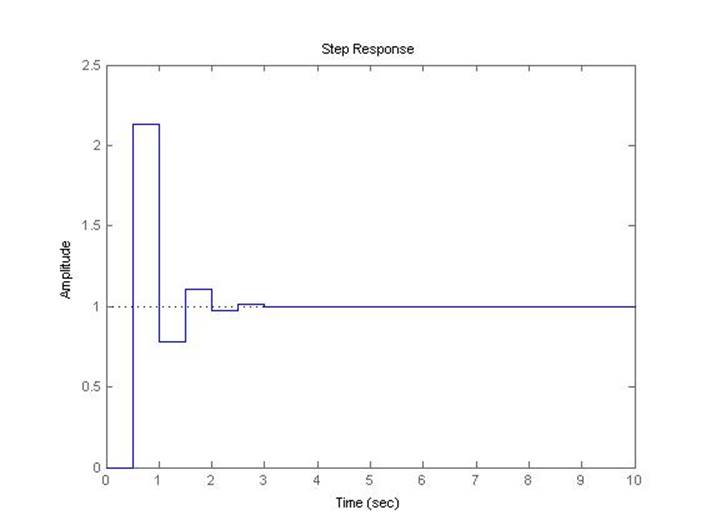
Рис.5.2.8. Осциллограмма выходного сигнала (К-0.8*предельный, шаг=0.5с).
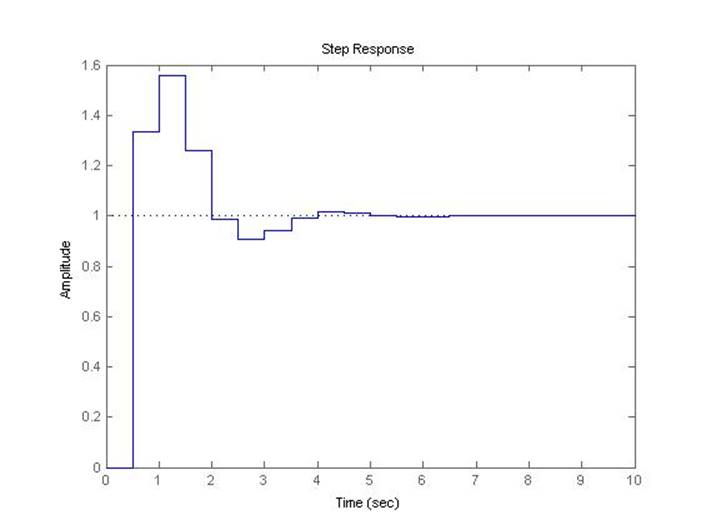
Рис.5.2.9. Осциллограмма выходного сигнала (К-0.5*предельный, шаг=0.5с).
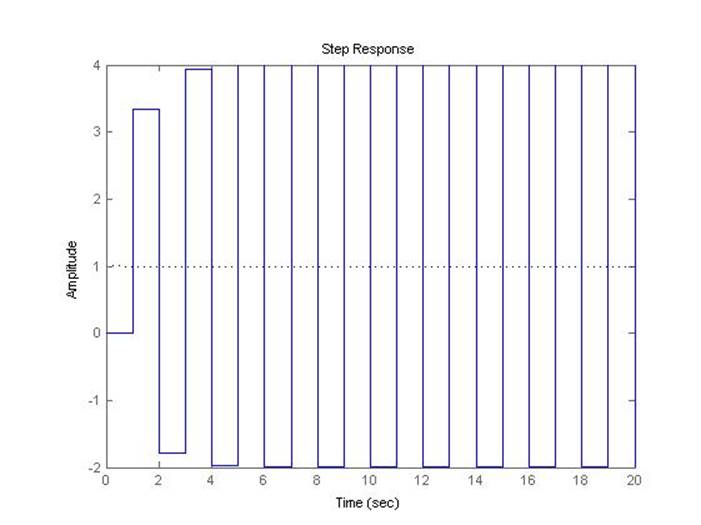
Рис.5.2.10. Осциллограмма выходного сигнала (К-предельный, шаг=1с).
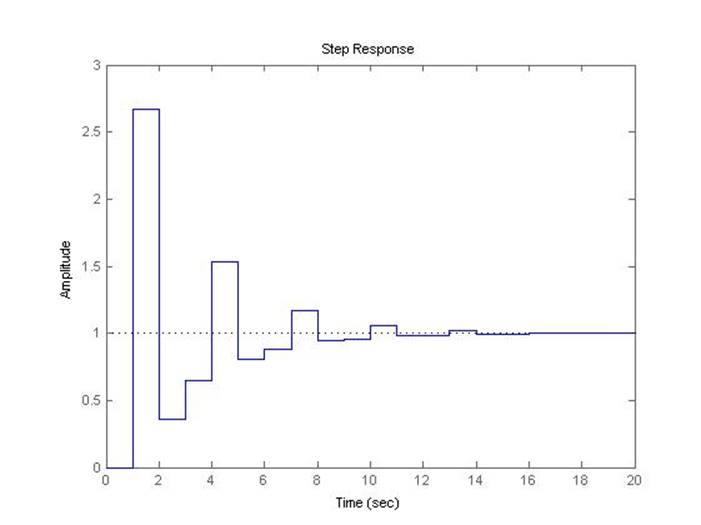
Рис.5.2.11. Осциллограмма выходного сигнала (К-0.8*предельный, шаг=1с).
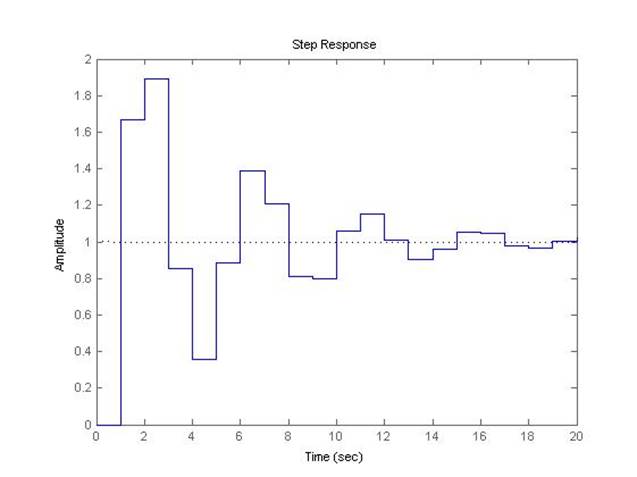
Рис.5.2.12. Осциллограмма выходного сигнала (К-0.5*предельный, шаг=1с).
5.3. Звено 3.
W(p) = k/p(Tp+1)
K = 5
T = 0.6
Дискретная передаточная функция системы с идеальным ключом и фиксатором на входе.
Дискретную передаточную функцию разомкнутой и замкнутой системы можно рассчитать из исходной непрерывной системы используя функции пакета Control System Toolbox Matlab.
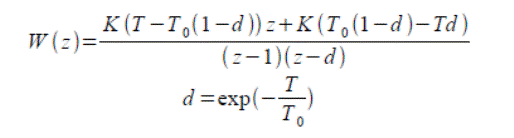
0.03945 z + 0.03731
W(z) = ----------------------
z^2 - 1.846 z + 0.8465
H(z) – передаточная функция замкнутой системы. Рассчитывается аналогично непрерывной системе.
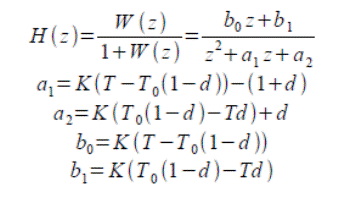
0.03945 z + 0.03731
W(z) = ----------------------
z^2 - 1.807 z + 0.8838
Расчет предельного значения K.
Сделаем замену переменных (билинейное преобразование) и применим критерий Гурвица.
Характеристическое уравнение системы:
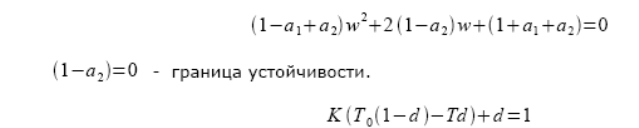
K=20.5711566…
Оптимального К не существует
Моделирование системы в Simulink.
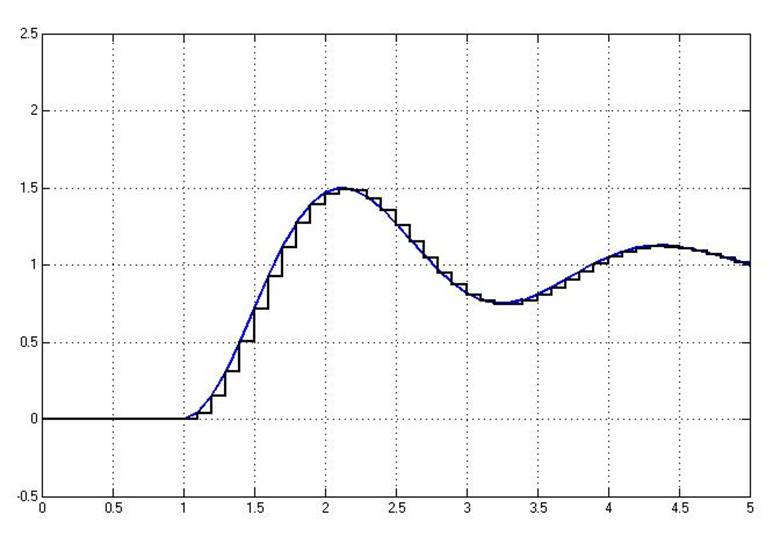
Рис.5.3.1. Осциллограмма выходных сигналов (К-5(заданный), шаг=0.1с).
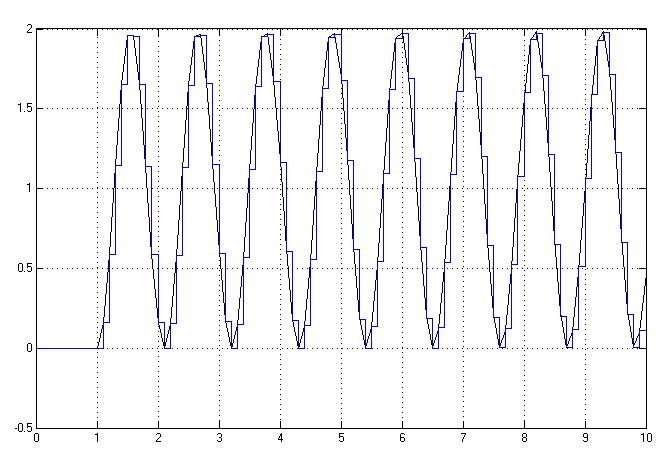
Рис.5.3.2. Осциллограмма выходных сигналов (К-предельный, шаг=0.1с).
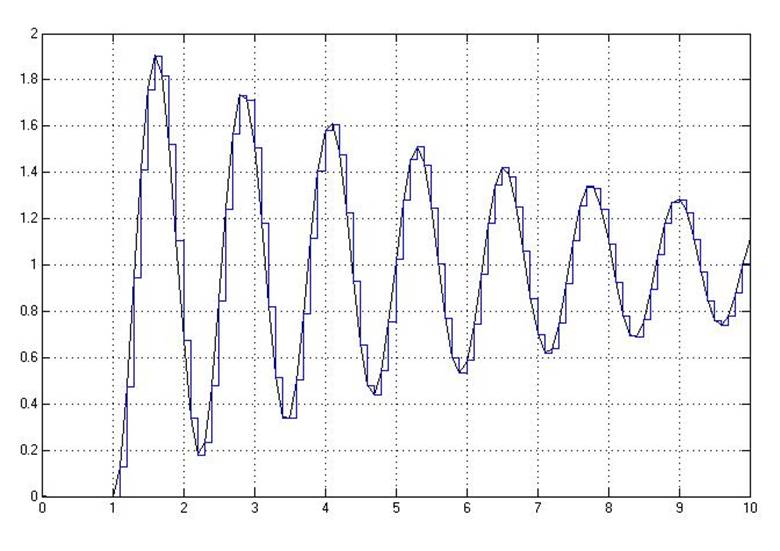
Рис.5.3.3. Осциллограмма выходных сигналов (К-0.8*предельный, шаг=0.1с).
Часть 2
Исследование влияния периода квантования на качество процессов.
Предельное значение периода квантования найдем из того же условия, что и предельное значение коэффициента усиления.
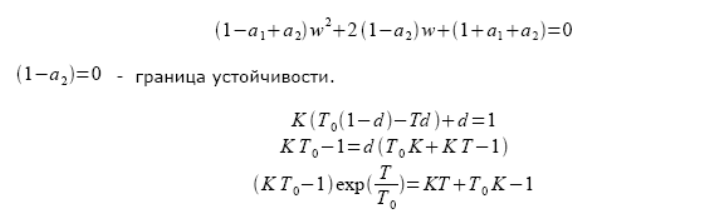
Уравнение решается численно функцией fzero.
Тпред = 0,4561313…
Предельные коэффициенты передачи системы получены подстановкой в предыдущую формулу.
Т=0,1с Кпр=20,57115..
Т=0,5с Кпр=4,63664…
Т=1с Кпр=2,7237..…
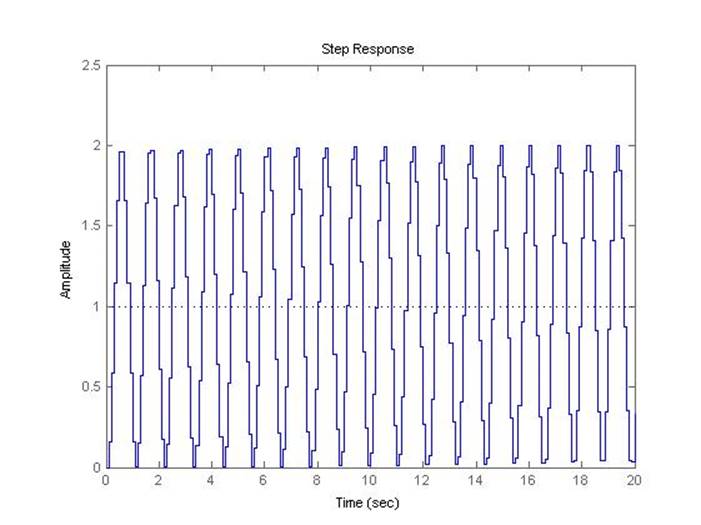
Рис.5.3.4. Осциллограмма выходного сигнала (К-предельный, шаг=0.1с).
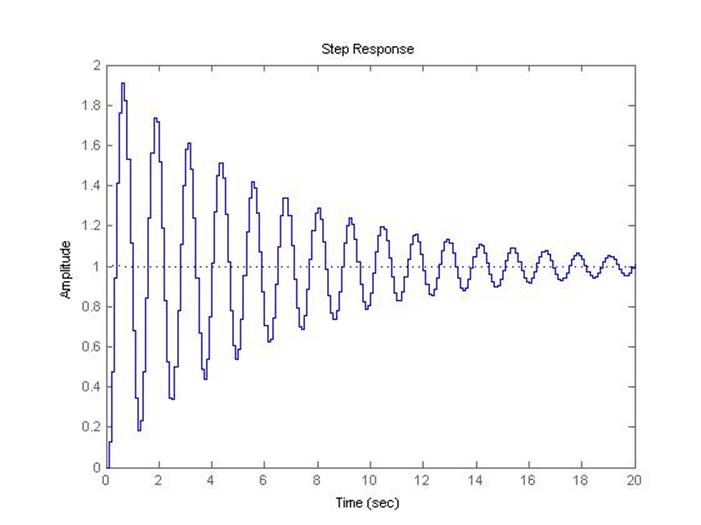
Рис.5.3.5. Осциллограмма выходного сигнала (К-предельный*0,8, шаг=0.1с).
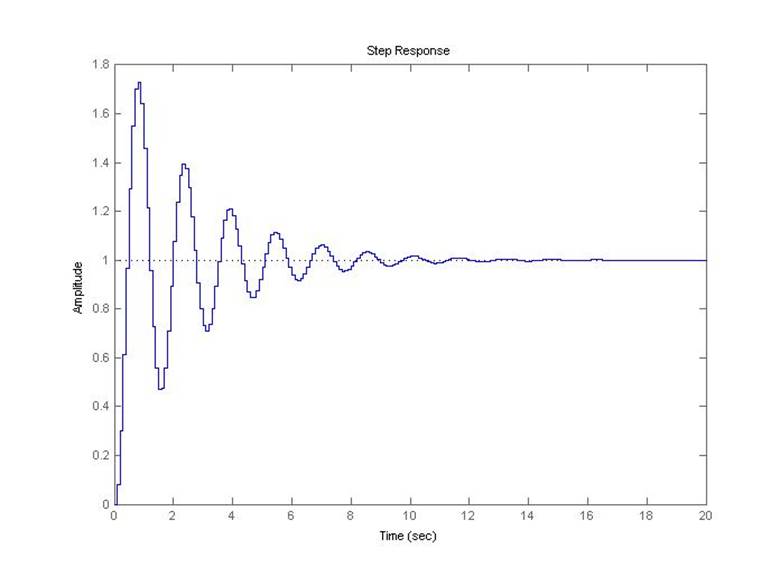
Рис.5.3.6. Осциллограмма выходного сигнала (К-предельный*0,5, шаг=0.1с).
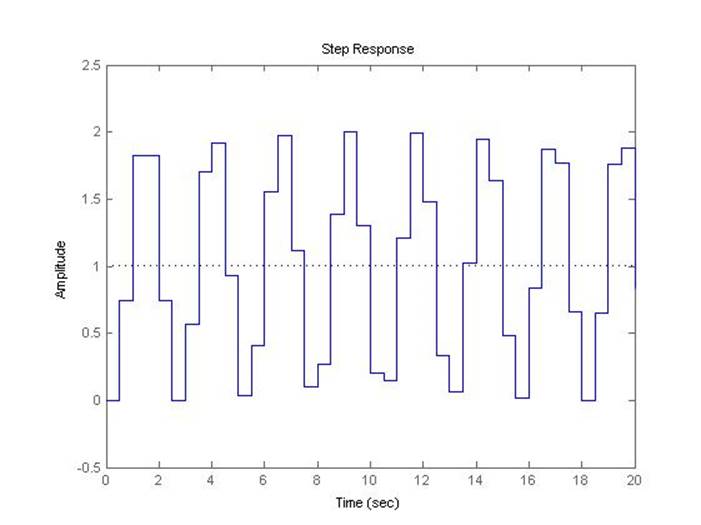
Рис.5.3.7. Осциллограмма выходного сигнала (К-предельный, шаг=0.5с).
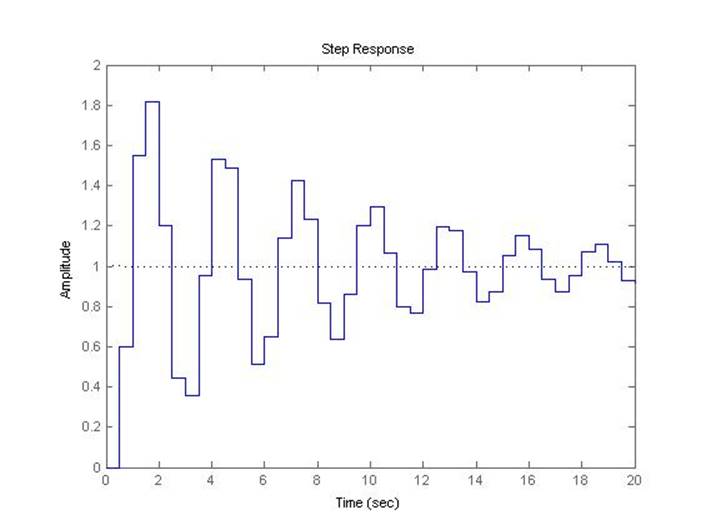
Рис.5.3.8. Осциллограмма выходного сигнала (К-предельный*0,8, шаг=0.5с).
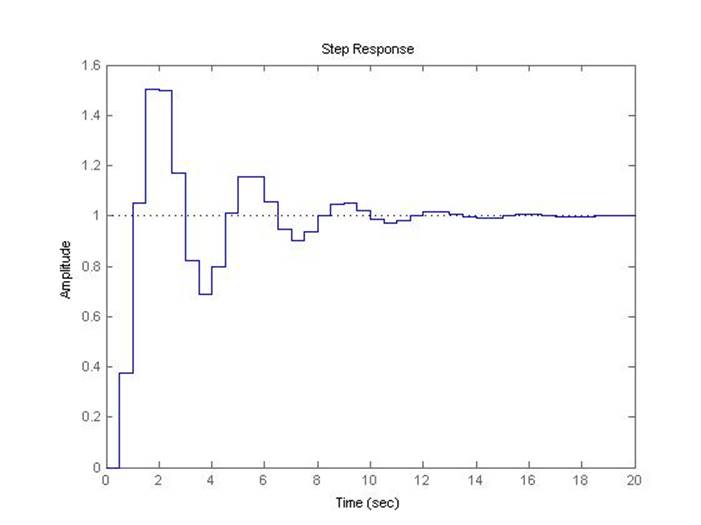
Рис.5.3.9. Осциллограмма выходного сигнала (К-предельный*0,5, шаг=0.5с).
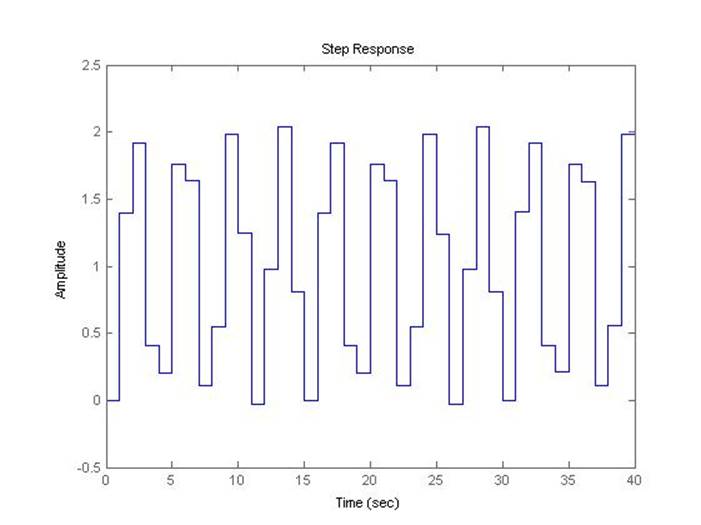
Рис.5.3.10. Осциллограмма выходного сигнала (К-предельный, шаг=1с).
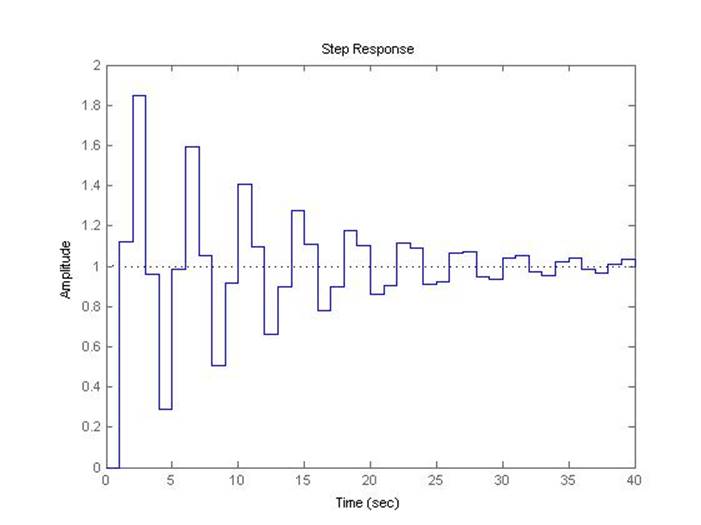
Рис.5.3.11. Осциллограмма выходного сигнала (К-предельный*0,8, шаг=1с).
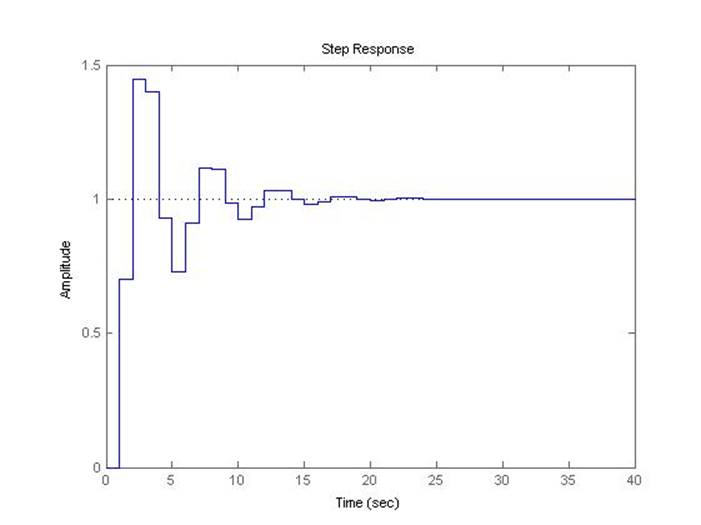
Рис.5.3.12. Осциллограмма выходного сигнала (К-предельный*0,5, шаг=1с).
6.Выводы.
Устойчивость и качество переходных процессов в дискретных системах так же как и в непрерывных зависит от параметров звеньев системы (таких как коэффициент усиления и постоянная времени).
Так же на динамические свойства дискретной системы большое влияние оказывает период квантования.
Предельные параметры звеньев и период интегрирования жестко связаны. Изменение периода квантования влияет на запасы устойчивости системы по одному из ее параметров.
Например, в рассмотренных первых двух системах при увеличении периода квантования запасы устойчивости системы по коэффициенту усиления уменьшаются.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.