Расчет оптимальной по быстродействию системы управления. Расчет оптимальной по быстродействию системы управления с ограничениями на управление

Санкт-Петербургский государственный политехнический университет

Факультет технической кибернетики

Кафедра автоматики и вычислительной техники

ОТЧЕТ ПО ЛАБОРАТОРНОЙ РАБОТЕ №2

Дисциплина: Теория оптимальных систем автоматического управления

Тема: Расчет оптимальной по быстродействию системы управления

Выполнил студент гр. 5081/2                                                                              

Руководитель                                                                                                          

Санкт-Петербург

2009

            1.         Постановка задачи

Необходимо построить временные характеристики переменных состояния и фазовый портрет оптимальной по быстродействию системы для двух случаев:

— Ограничения наложены только на управление

— Ограничения наложены на управление и на переменные состояния.

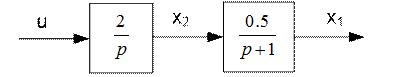
Рис. 1. Структурная схема системы управления

Ограничения на управление: .

Ограничения на переменные состояния:

Начальные значения переменных состояния:

в момент времени t = 0:      X₂ = 0, X₁ = -5;         

В момент времени t = T:     X₂ = X₁ = 0.

2.         Расчет оптимальной по быстродействию системы управления с ограничениями на управление

Так как система управления является линейной системой второго порядка, то управление будет релейным с двумя моментами переключения: t = 0, t = t₁.

Заданную систему управления описывает следующая система дифференциальных уравнений:

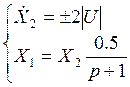
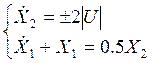
1) Т.к. начальные условия переменных состояния отрицательны, то на первом участке управление положительное: u= 1. Тогда система уравнений для первого участка:

    

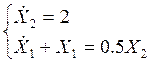
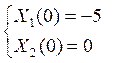
Решив систему дифференциальных уравнений

dsolve('Dy=2,Dx+x=0.5*y','y(0)=0,x(0)=-5', 't'), найдем функции времени переменных состояния на первом участке:

 

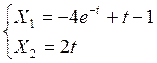
2) На втором участке управление принимает значение U = -1:

 

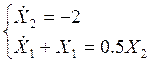
Функции времени переменных состояния на втором участке

dsolve( 'Dy=-2,Dx+x=0.5*y', 't'):

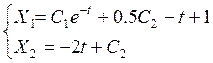
С₁ и С₂ определяются начальными условиями.

Таким образом, необходимо определить константы С₁ и С₂, а также момент переключения t₁ и момент окончания управления T. Система уравнений для нахождения параметров:

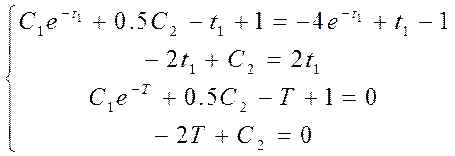
Решив эту систему

Y = solve ('C1*exp(-t1)+0.5*C2-t1+1 = -4*exp(-t1)+t1-1', '-2*t1+C2 = 2*t1', 'C1*exp(-T)+0.5*C2-T+1 = 0', '-2*T+C2 = 0'), получим:

С₁ = -10.472135954999579392818347337463

С₂ = 4.6974360224781950276599641395302

t₁ = 1.1743590056195487569149910348826

T = 2.3487180112390975138299820697651

Т.о. функции времени переменных состояния на втором участке:

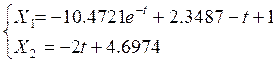
Временные характеристики управления и переменных состояния представлены на    рис.2.1-2.2. Фазовый портрет системы представлен на рис. 2.3.

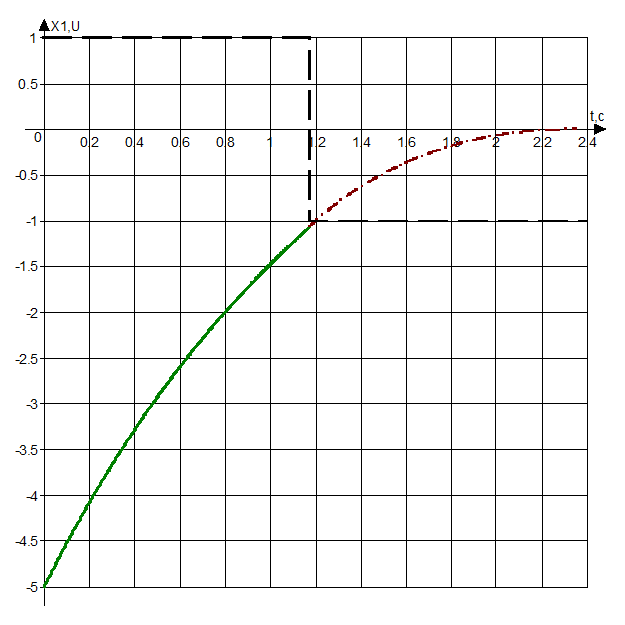
Рис. 2.1. Временная характеристика X1(t)

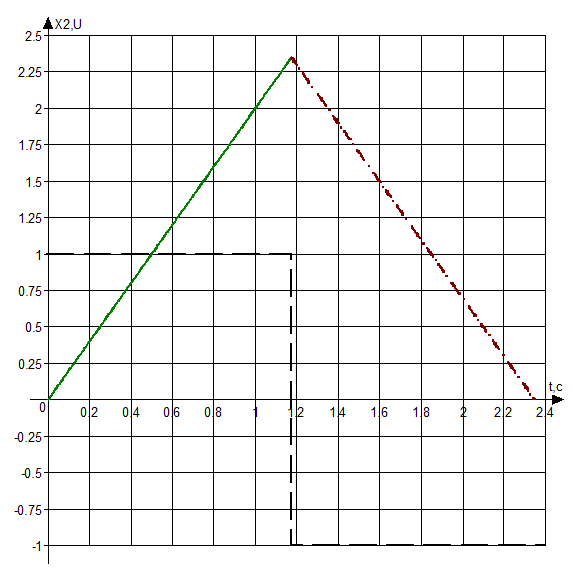
Рис. 2.2. Временная характеристика X2(t)

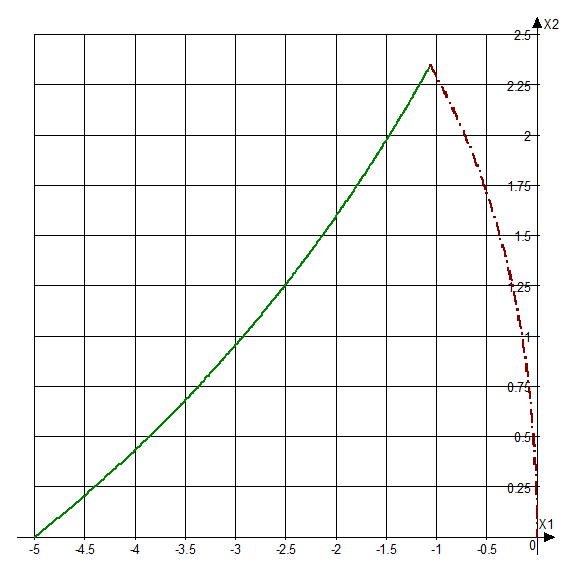
Рис. 2.3. Фазовый портрет системы

3.         Расчет оптимальной по быстродействию системы управления с ограничениями на управление и переменные состояния

Ограничения на управление: .

Ограничения на величину переменных состояния:

Т.к. система управления является линейной системой второго порядка, то управление будет релейным с тремя участками переключения.

Заданную систему управления описывает следующая система дифференциальных уравнений:

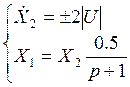
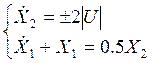
1) Т.к. начальные условия переменных состояния отрицательны, то на первом участке управление положительное: u= 1. Тогда система уравнений для первого участка:

    

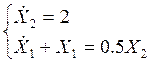
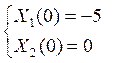
Решив систему дифференциальных уравнений, найдем функции времени переменных состояния на первом участке:

 

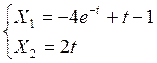
2) Второй участок управления:

Переменная состояния X₂ на временном отрезке постоянна и равна 1, а значит ее производная равна 0. Тогда система уравнений для второго участка:

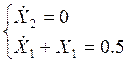
Дифференциальное уравнение для переменной состояния X₁:

Функция времени переменных состояния на втором участке:

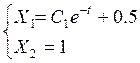
С₁ определяется начальными условиями для этого участка.

3) Третий участок управления:

На третьем участке управление отрицательное: u=-1. Тогда система уравнений для этого участка:

 

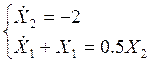
Функции времени переменных состояния на третьем участке:

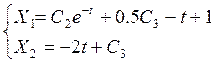
С₂  и С₃  определяются начальными условиями для этого участка.

Таким образом, необходимо определить константы С₁, С₂ и С₃,а также моменты переключения t₁ и t₂ и момент окончания управления T. Система уравнений для нахождения параметров:

 

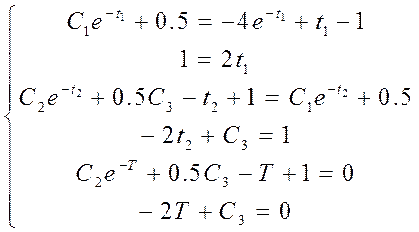
Решив эту систему

Y = solve ('C1*exp(-t1)+0.5 = -4*exp(-t1)+t1-1', '1 = 2*t1', 'C2*exp(-t2)+0.5*C3-t2+1 = C1*exp(-t2)+0.5', '-2*t2+C3=1', 'C2*exp(-T)+0.5*C3-T+1=0', '-2*T+C3=0'), получим:

С₁ = -5.6487212707001281468486507878142

С₂ = -14.356191683384119567504168010177

С₃ = 5.3283626506811199463407603216815

t₁ = 0.5

t₂ = 2.1641813253405599731703801608408

T = 2.6641813253405599731703801608408

Т.о. функции времени переменных состояния на втором участке:

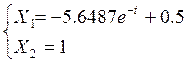
Функция времени переменных состояния на третьем участке:

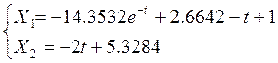
Временные характеристики управления и переменных состояния представлены на    рис.3.1-3.2. Фазовый портрет системы представлен на рис. 3.3.

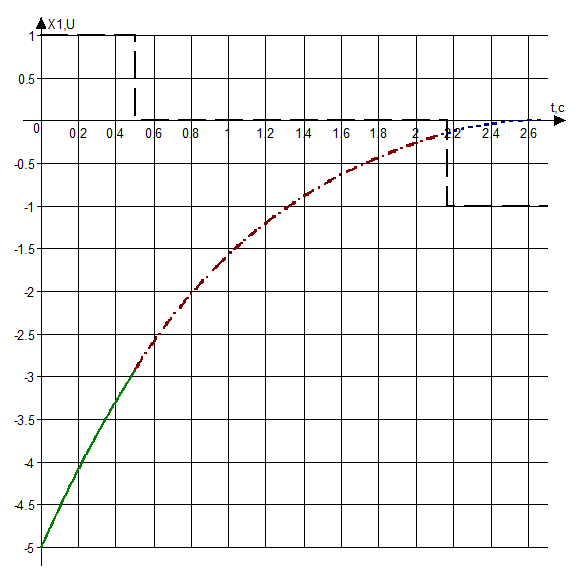
Рис 3.1. Временная характеристика X₁(t)

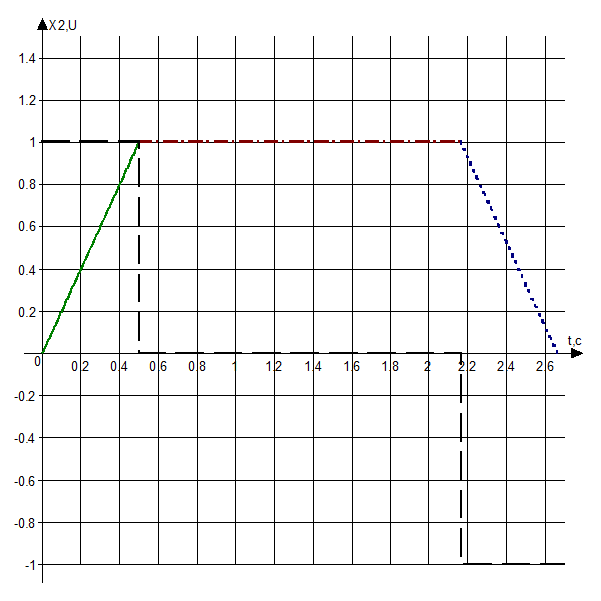
Рис. 3.2. Временная характеристика X₂(t)

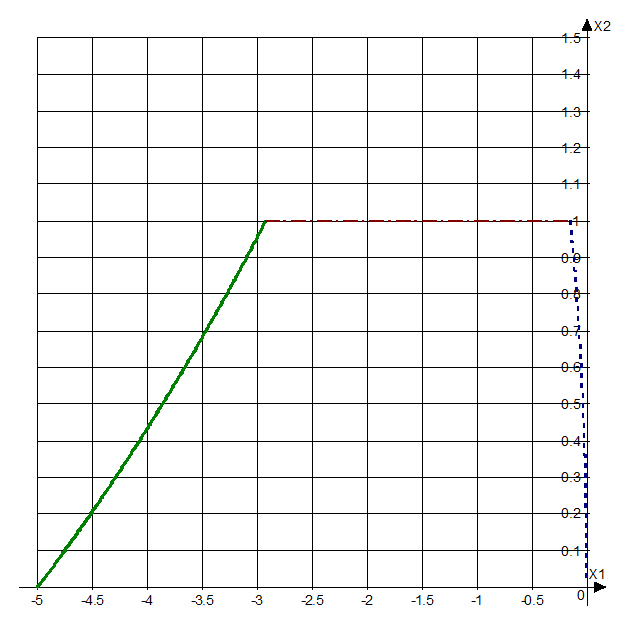
Рис. 3.3. Фазовый портрет системы