Фазовые траектории динамических систем. Изучение процессов в нелинейных системах с помощью фазовой плоскости

Санкт-Петербургский государственный политехнический университет

Факультет технической кибернетики

Кафедра компьютерных систем и программных технологий

Отчет по лабораторной работе №10

(Учебная дисциплина «Теория автоматического управления»)

Фазовые траектории динамических систем

Работу выполнил студент группы №4081/2                     

Работу принял преподаватель___________                                    

Санкт-Петербург

2010

1. Цель работы.

Изучение процессов в нелинейных системах с помощью фазовой плоскости.

2. Исследуемая система.

Структурная схема исследуемой системы.

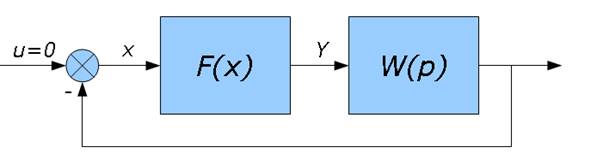
Рис 2.1. Структурная схема системы.

F(x) — нелинейное звено, с кусочно-линейной нелинейностью типа «зона нечувствительности». Характеристика нелинейности имеет вид:

       

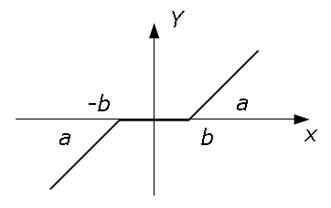
Рис 2.2. Характеристика нелинейности.

W(p) – линейное звено, имеющее передаточную функцию:

3. Исходные данные.

K = 2, 5, 10;

T = 0.1 c, 0.5 c, 1 c;

b = 1;

tg a = 1;

4. Исследование фазовых траекторий в Simulink.

Схема моделирования системы с отрицательной обратной связью. Входной сигнал отсутствует.

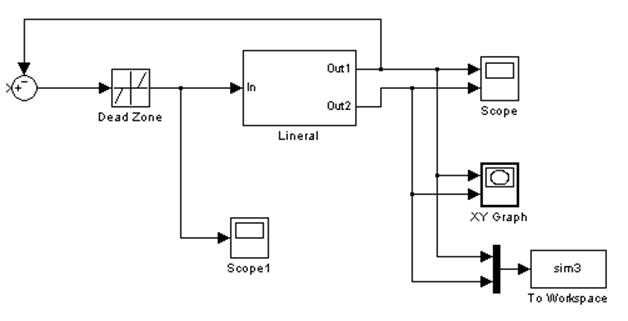
Рис. 4.1. Схема моделирования в Simulink.

Блок Lineral содержит линейную часть системы.

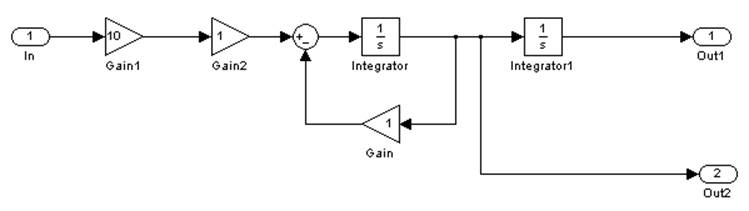
Рис. 4.2. Структурная модель линейной части системы.

Линейная часть системы представлена структурной моделью для того, чтобы можно было задавать различные начальные условия моделирования.

Начальные условия задаются в блоках интеграторов.

Выходы блока Lineral это соответственно выходной сигнал системы (Out1) и его производная (Out2).

5. Фазовые портреты системы и переходные процессы, при различных параметрах системы.

K = 5, T = 0.1:

Фазовые траектории.

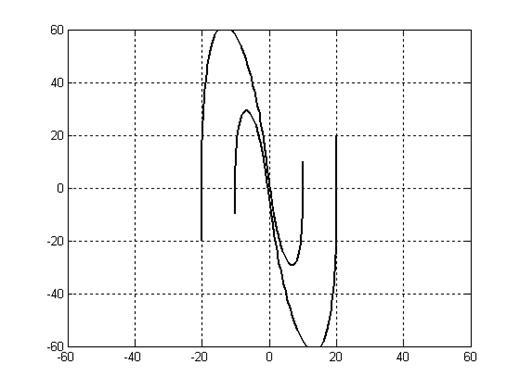
Рис. 5.1.

Переходный процесс, начальные условия (10,10).

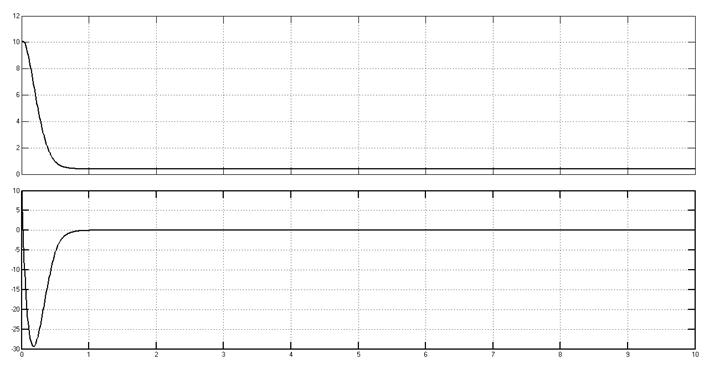
Рис. 5.2.

Фазовая траектория соответствует устойчивому процессу с одним перерегулированием. Установившееся состояния системы  определяется не началом координат, а отрезком зоны нечувствительности.

K = 5, T = 0.5:

Фазовые траектории.

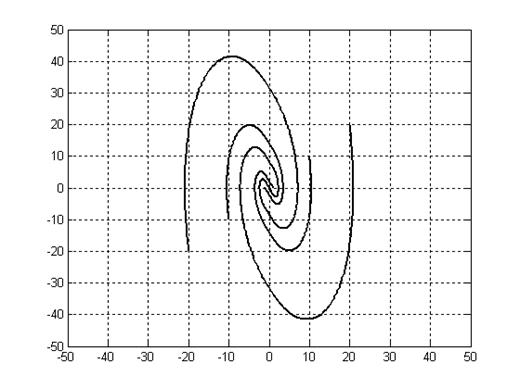
Рис. 5.3.

Переходные процессы, начальные условия (10,10).      

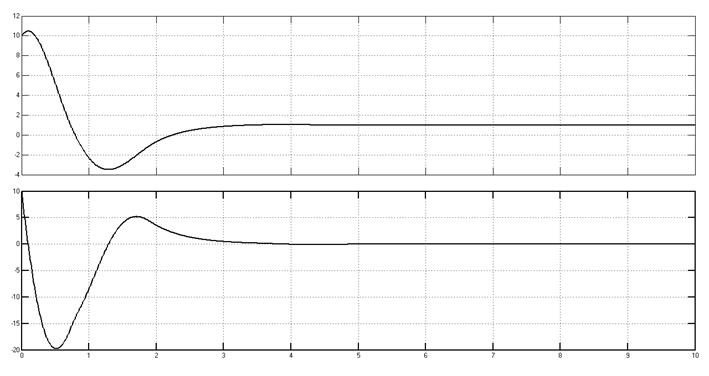
Рис. 5.4.

K = 5, T = 1:

Фазовые траектории.

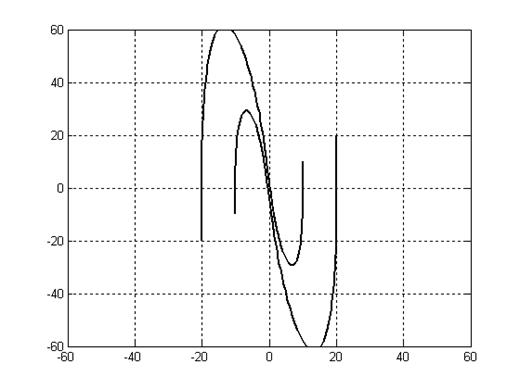
Рис. 5.5.

Переходные процессы, начальные условия (10,10).      

Рис. 5.6.

K = 2, T = 0.5:

Фазовые траектории.

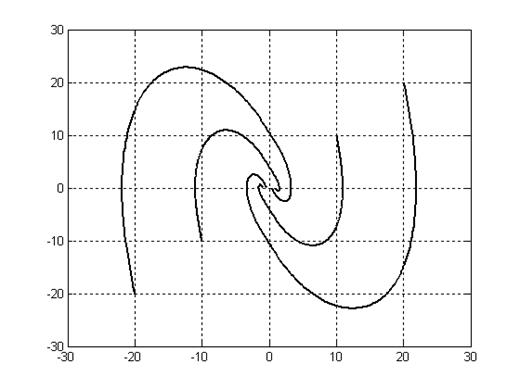
Рис. 5.7.

Переходные процессы, начальные условия (10,10).       

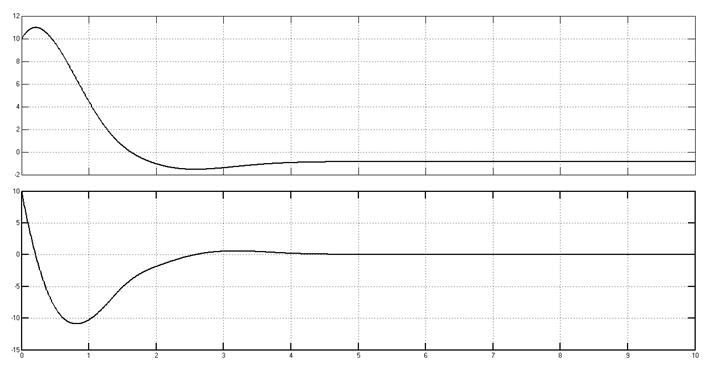
Рис. 5.8.

K = 10, T = 0.5:

Фазовые траектории.

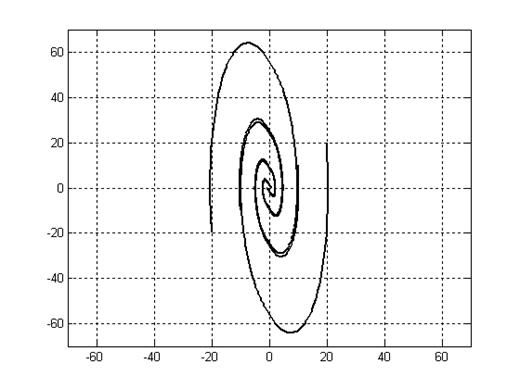
Рис. 5.7.

Переходные процессы, начальные условия (10,10).       

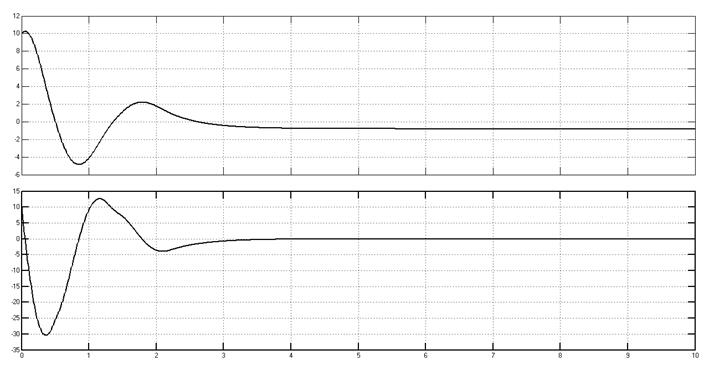
Рис. 5.8.

6. Система с обратной связью по производной выходного сигнала.  

Введем на вход не вход нелинейного звена дополнительный сигнал обратной связи по производной выходного сигнала и рассмотрим фазовые траектории системы.

Схема моделирования системы с обратной связью по производной.

       

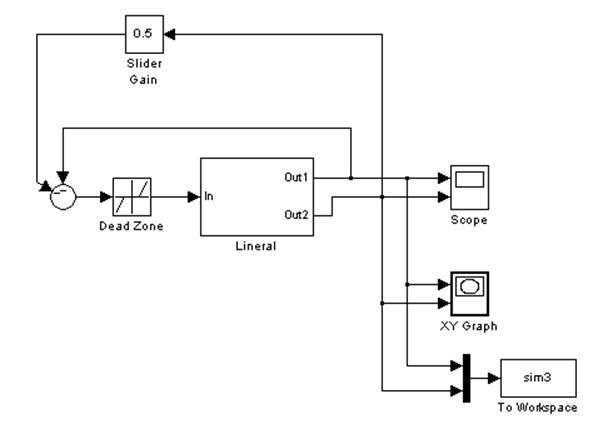
Рис. 6.1. Схема моделирования в Simulink.

Рассмотрим, как изменится фазовый портрет системы и переходные процессы после изменения структуры системы.

K = 5, T = 0.5, К_ос = -0.5:

Фазовые траектории.

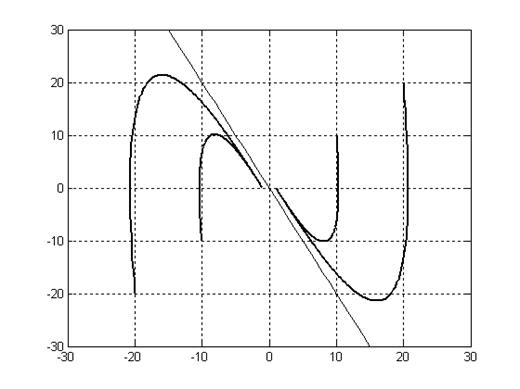
Рис. 6.2.

Переходные процессы, начальные условия (10,10).

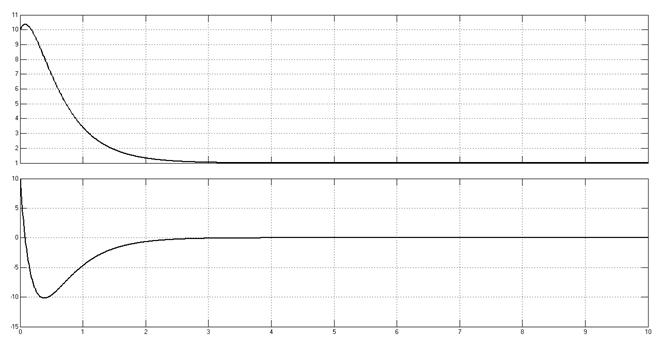
Рис. 6.3.

K = 5, T = 0.5, К_ос = -1:     

Фазовые траектории.

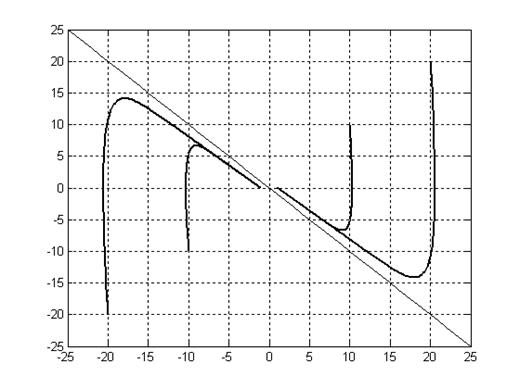
Рис. 6.4.

Переходные процессы, начальные условия (10,10).

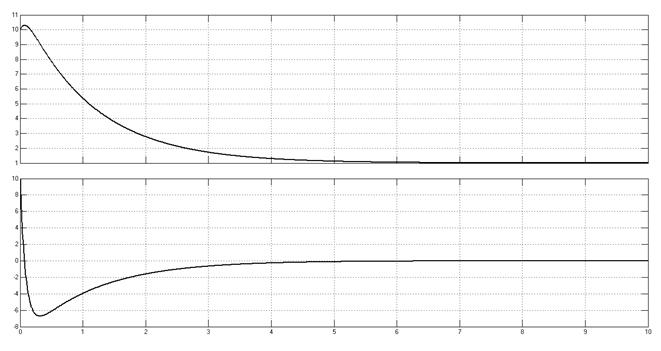
Рис. 6.5.

По сравнению с системой без обратной связи по производной входного сигнала, данная система имеет переходные процессы с меньшей колебательностью и перерегулированиями.

При изменении знака обратной связи по скорости изменения выходного сигнала при определенных значениях коэффициента обратной связи можно получить установившиеся гармонические колебания.

K = 5, T = 0.5, К_ос = 0.2:

Фазовые траектории.

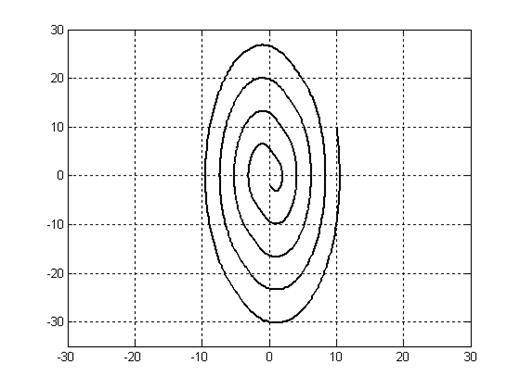
Рис. 6.6.

Переходные процессы, начальные условия (10,10).

       

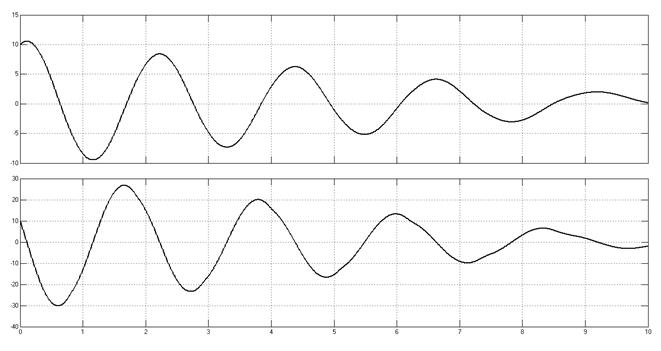
Рис. 6.7.

K = 5, T = 0.5, К_ос = 0.2215:

Фазовые траектории.

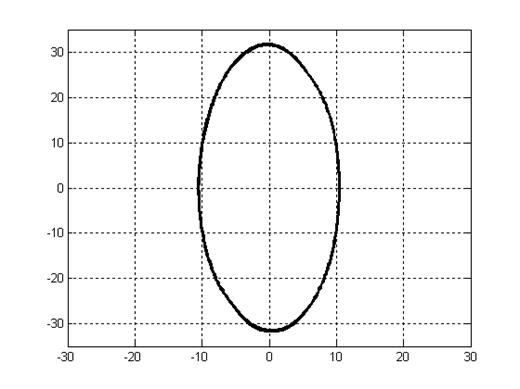
Рис. 6.8.

Переходные процессы, начальные условия (10,10).

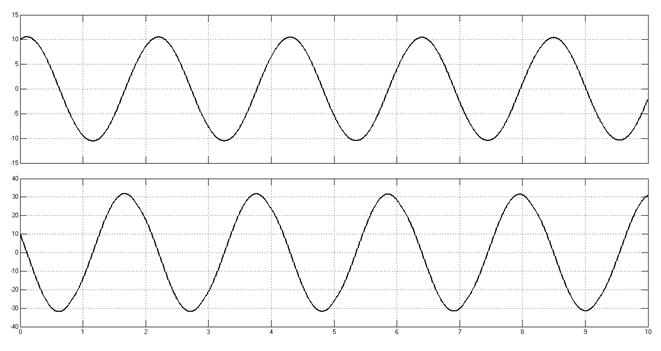
Рис. 6.9.

K = 5, T = 0.5, К_ос = 0.23:

Фазовые траектории.

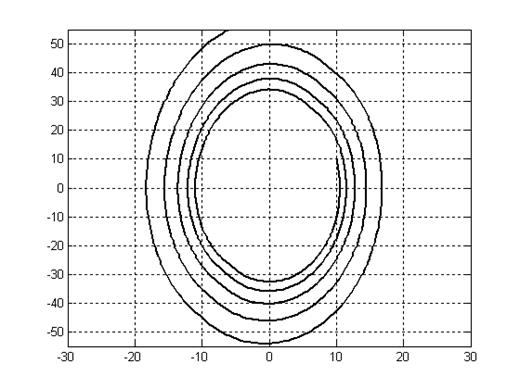
Рис. 6.10.

Переходные процессы, начальные условия (10,10).

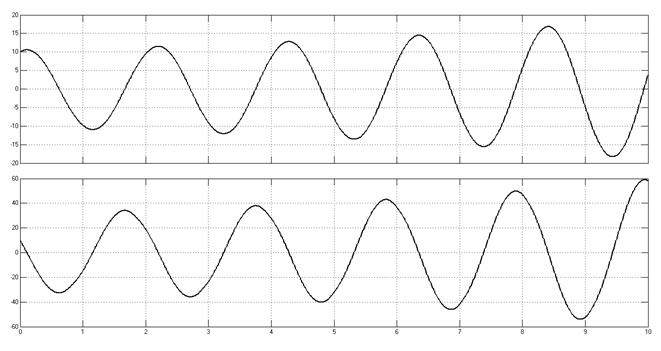
Рис. 6.11.

Динамика нелинейных систем зависит от начальных условий, вот например в если последнем случае изменить начальные условия на (5, 5), то колебательный процесс будет не расходящимся, а затухающим.

Фазовые траектории.

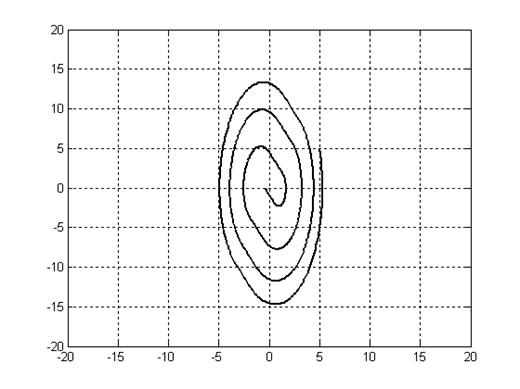
Рис. 6.12.

Переходные процессы, начальные условия (5, 5).

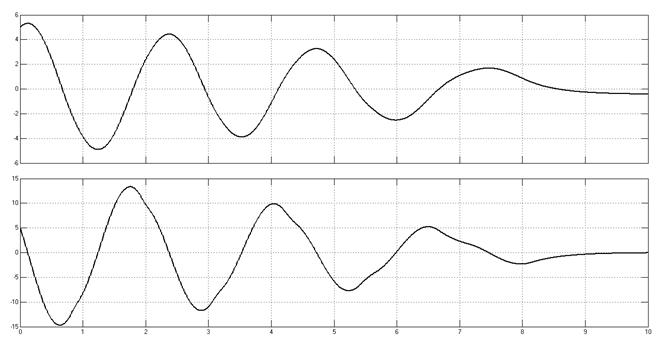
Рис. 6.13.

7. Выводы и анализ результатов работы.

По результатам работы можно сделать следующие выводы.

Фазовые портреты системы и характер протекания переходных процессов зависит от структуры самой системы. Так при изменении коэффициента усиления линейной части системы и постоянной времени, введении дополнительной обратной связи по скорости изменения входного сигнала, происходит изменение фазовых портретов и характер переходных процессов.

Первая рассмотренная система (без обратной связи по скорости изменения выходного сигнала) является устойчивой. Устойчивое положение определяется не началом координат, а отрезком зоны нечувствительности.

При введении обратной связи по скорости изменения выходного сигнала фазовые портреты и характер переходных процессов в  системе изменяются.

Так, при положительной обратной связи можно получить установившиеся гармонические колебания.