Характеристическое уравнение располагается в последней строке.
9
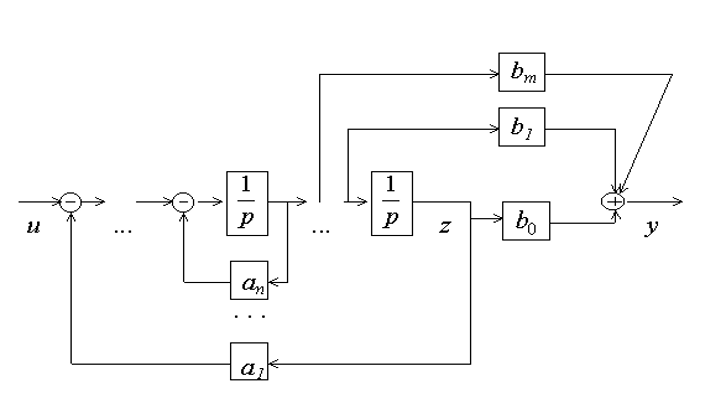
Структурная схема для управляемой канонической формы уравнений состояния
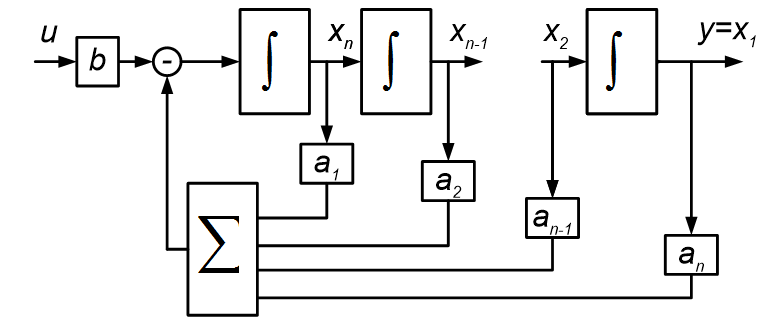
…
Здесь переменные состояния – фазовые координаты.
10
Другая форма: в правой части уравнения содержатся производные от входного воздействия
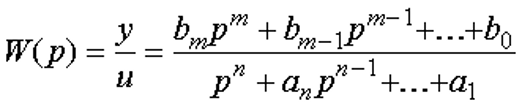
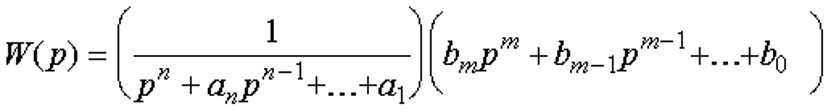

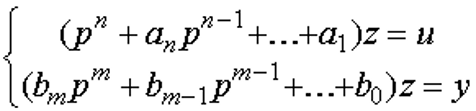
11
Введем переменные состояния:
Здесь координаты состояния xi – абстрактные переменные.
12
Этим уравнениям соответствует структура:
13
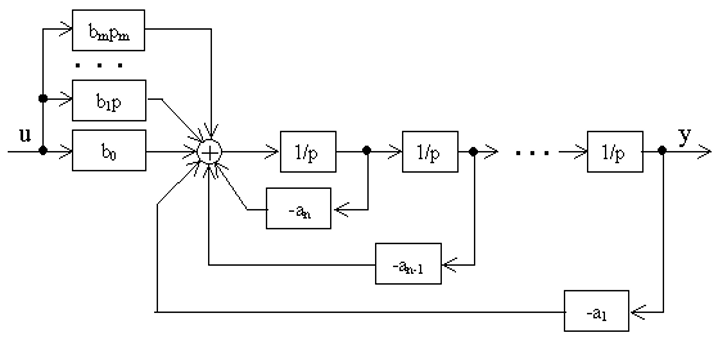
Возможно другое представление:

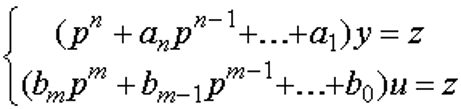
14
Структурная схема может быть преобразована к виду:
15
Тогда матрицы A, B, C в уравнениях состояния будут:
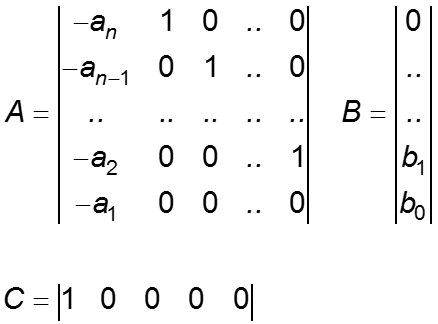
Это - наблюдаемая каноническая форма уравнений состояния.
Таким образом, переход от передаточной функции к описанию в переменных состояния является неоднозначным.
16
Другие канонические формы уравнений состояния.
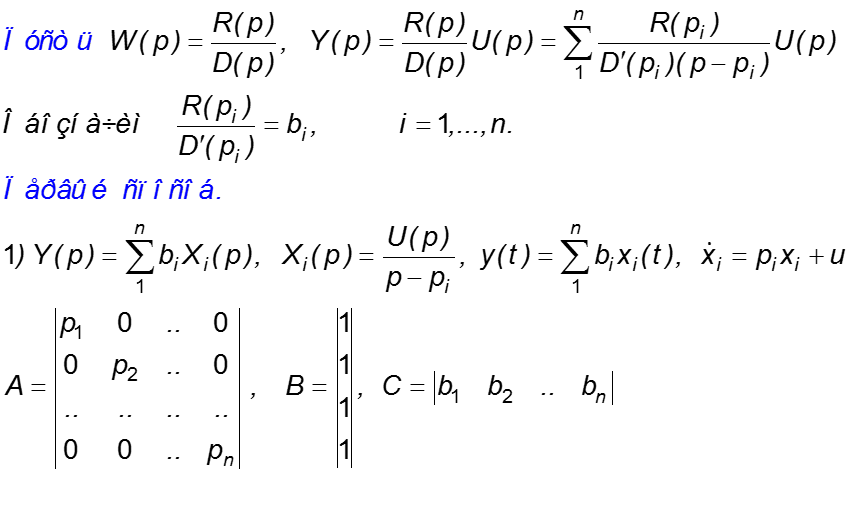
17
Второй способ.
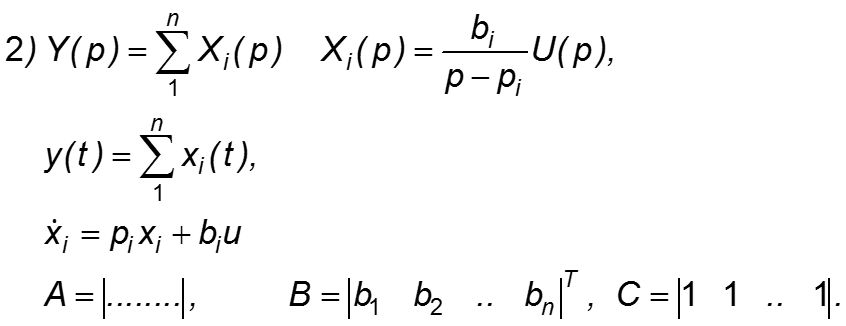
В двух последних формах матрица А – диагональная.
18
19
Пример получения уравнений состояния
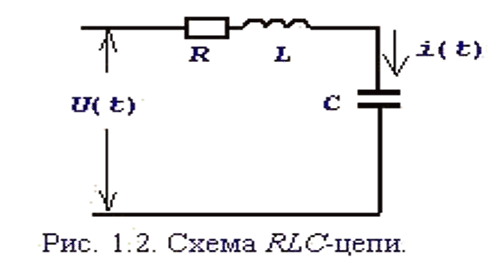
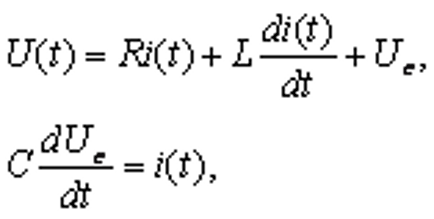
Уравнения состояния:
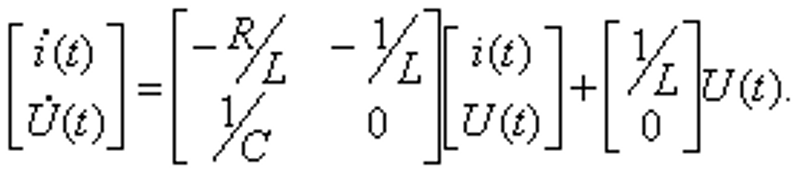
20
П р и м е р. Система описывается дифференциальным уравнением Составим уравнения состояния и структурную схему
21
Свойства объектов и систем управления. Управляемость .
Определение. Система полностью управляема, если она может быть переведена из любого начального состояния x(0) в начало координат (0, 0,…,0) под действием управления u(t) за конечное время. Теорема Калмана об управляемости. Состояние непрерывной системы управляемо, если и только если ранг матрицы NУ = [B | AB | A2B | ... | An-1B] равен размерности пространства состояний n.
22
Пример 1. Проверим, управляема ли система:
23
Пример 2. Также проверим управляемость системы:
24
Пример 3.
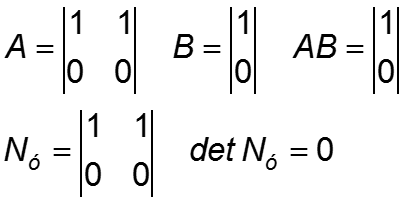
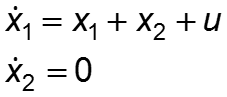
Т.к. rangNy = 1 , система управляема неполностью. Порядок управляемой части равен 1.
В такой системе есть “висячая” часть на входе.
25
В случае представления объекта управления моделью типа “вход - выход” условием его управляемости является отсутствие общих корней полиномов А(p) и B(p): Т.е. система управляема, если алгебраические уравнения A(p)=a0pn+a1pn-1+…+an = 0, B(p)=b0pm+b1pm-1+…+bm = 0 не имеют общих корней.
![]()
Рассмотрим пример.
26
Пример 2. Определим управляемость системы, имеющей передаточную функцию
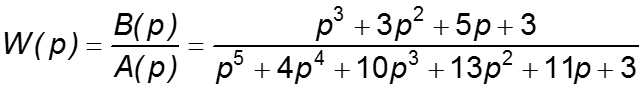
Прямой расчет корней числителя и знаменателя дает результаты, приведенные в табл.

Таким образом, числитель и знаменатель передаточной функции W(p) имеют два общих корня (-1 -j1.414) и ( -1+j 1.414). Значит, система не управляема. Изменение значений корней для этих пар в числителе или знаменателе переведет систему в ранг управляемых.
27
Наблюдаемость
28
Наблюдаемость
Упражнение.
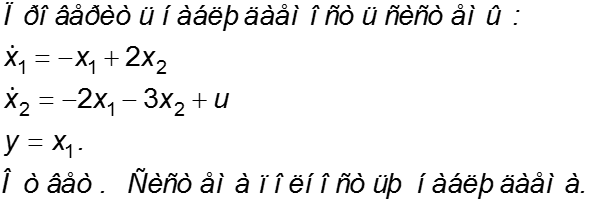
29
Пример 2.
30
31
Изменение базиса в уравнениях состояния
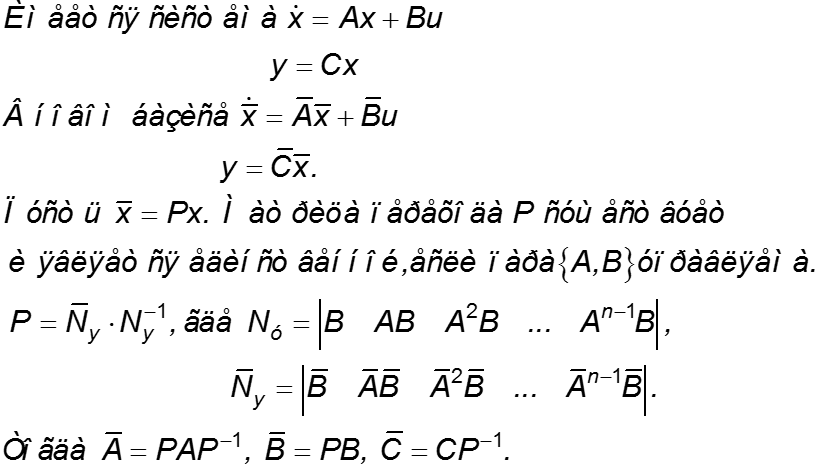
32
Пример (упражнение)
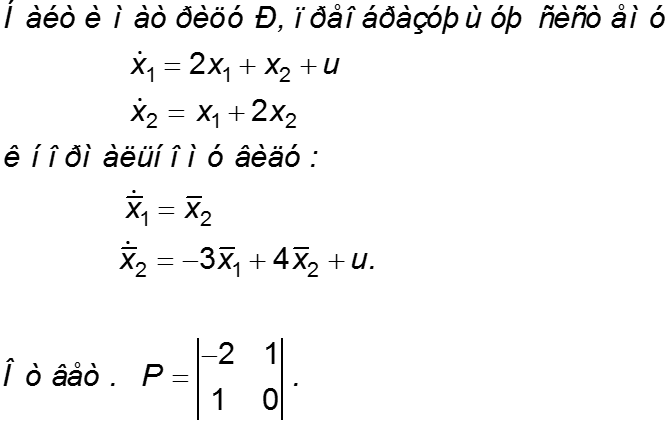
33
О синтезе системы
34
35
Распределение полюсов системы управления
36
37
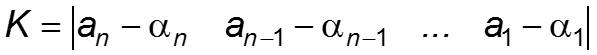


38
Пример
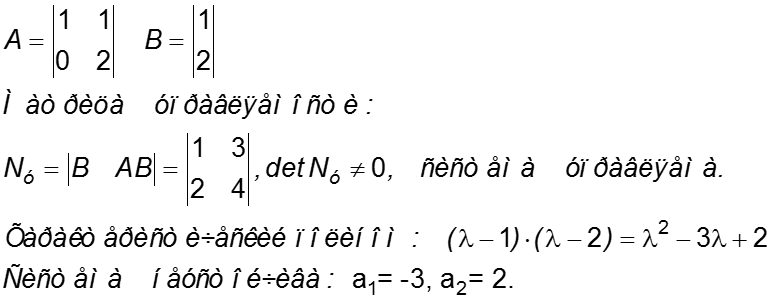
Нормальная форма матрицы А:
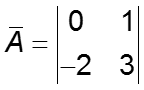
39
Пусть желаемые полюсы : λ1= -3, λ2= -2 Желаемый характеристический полином: φ=(λ+3)(λ+1)= λ 2+4 λ +3; α1=4, α2=3. Тогда k1 = a2 - α2 = 2 - 3 = -1, k2 = a1- α1 = -3 - 4 = -7. K = |-1 -7| Следовательно: v = u - x1 -7x2 Вычислив матрицу перехода P от исходной к нормальной форме можно получить матрицу обратной связи для исходного представления
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.