Исследование устойчивости разомкнутой и замкнутой системы. Необходимое и достаточное условие устойчивости

1. Исследование устойчивости разомкнутой и замкнутой системы.

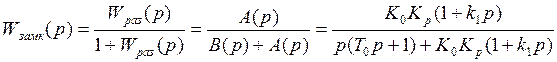
1) Устойчивость разомкнутой системы определяется корнями D(p)  ( Q(p) ):

p = 0                          – на границе устойчивости

p = -1/T0 = -0,2 < 0

Необходимое и достаточное условие устойчивости состоит в том, чтобы вещественные части всех корней характеристического уравнения были бы отрицательными.

2) Устойчивость замкнутой системы определим по знакам характеристического уравнения:

 - для системы 2 порядка положительность коэффициентов является необходимым и достаточным условием устойчивости.

Замкнутая система устойчива.

2. Построение границ областей устойчивости в плоскости параметров .

Выделение областей устойчивости в плоскости двух параметров:

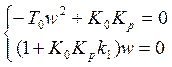
Обозначим: А – T0, В – k1

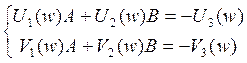
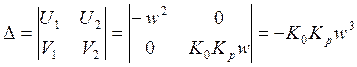
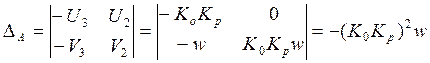
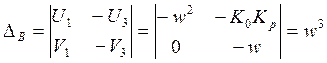
Листинг 2.1. Выполнение построения  областей устойчивости в плоскости параметров системы в Matlab’е.

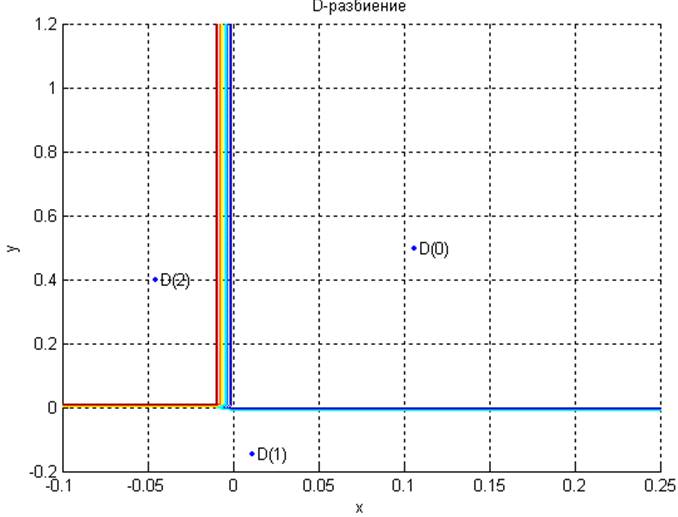
Рис 2.1. Области устойчивости в плоскости двух параметров системы

Система устойчива только в области параметров D(0).

( область D(1) – T0 < 0, область D(2) – k1 < -1/120 )

3. Построение линий равной степени устойчивости в плоскости тех же параметров.

     

 

Листинг 3.1. Файл с исходными данными (data.m), для выполнения функции Rtanalti в Matlab’е.

a(1) и a(2) – варьируемые параметры (k₁  и T0 оответственно ).

Листинг 3.2. Выполнение построения  линии равной степени устойчивости в плоскости тех же параметров в Matlab’е.

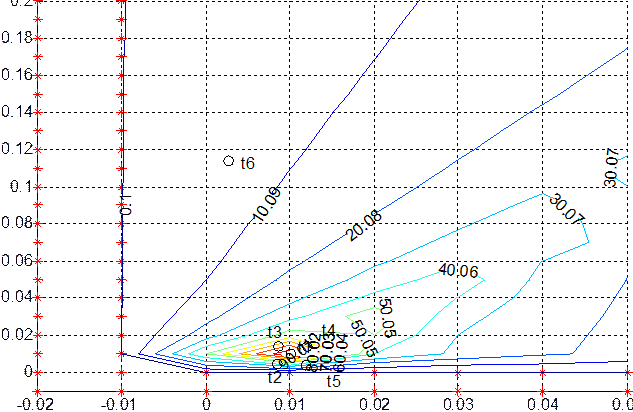
Рис 3.1. Линии равной степени устойчивости

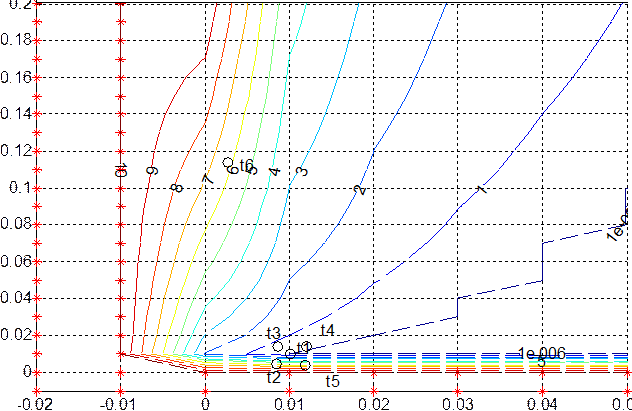
Рис 3.2. Линии равной степени колебательности

4. Построение переходного процесса для единичного ступенчатого воздействия на входе при нулевых начальных условиях для оптимальных значений параметров. Определение показателей качества переходного процесса.

Исследование чувствительности системы к изменению этих параметров.

Амплитуда

t,c

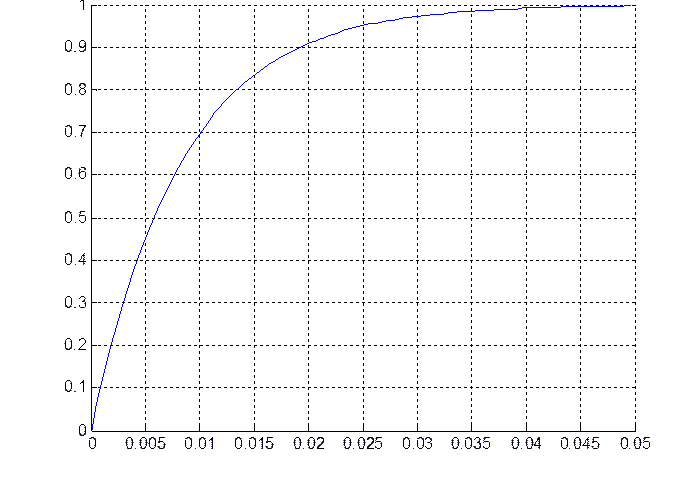
Рис.4.1. Переходная характеристика на выходе инерционного пропорционально дифференцирующего звена при ступенчатом входном воздействии (для первой точки – t1).

Текущие значения параметров системы:

a1 = 0.010141

a2 = 0.010125

Значение степени устойчивости: 97.924376

Значение степени колебательности: 0.000000

Величина перерегулирования: 0 %

Время переходного процесса: 0.025 с

Амплитуда

t,c

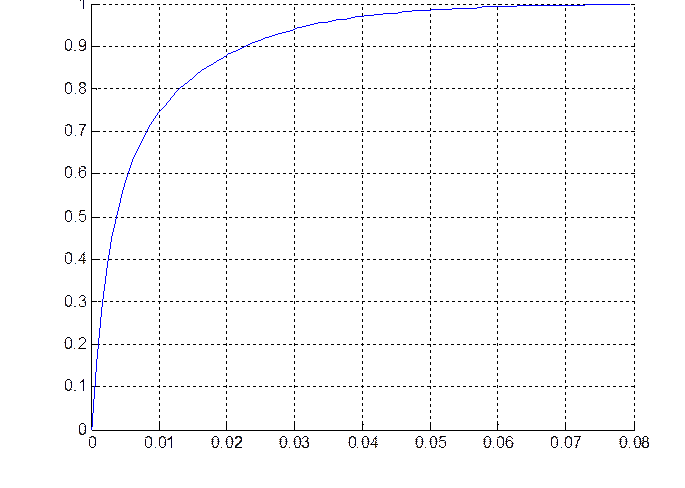
Рис.4.2. Переходная характеристика на выходе инерционного пропорционально дифференцирующего звена при ступенчатом входном воздействии (для второй точки – t2).

Текущие значения параметров системы:

a1 = 0.008446

a2 = 0.004392

Значение степени устойчивости: 70.408383

Значение степени колебательности: 0.000000

Величина перерегулирования: 0 %

Время переходного процесса: 0.03 с

Амплитуда

 t,c

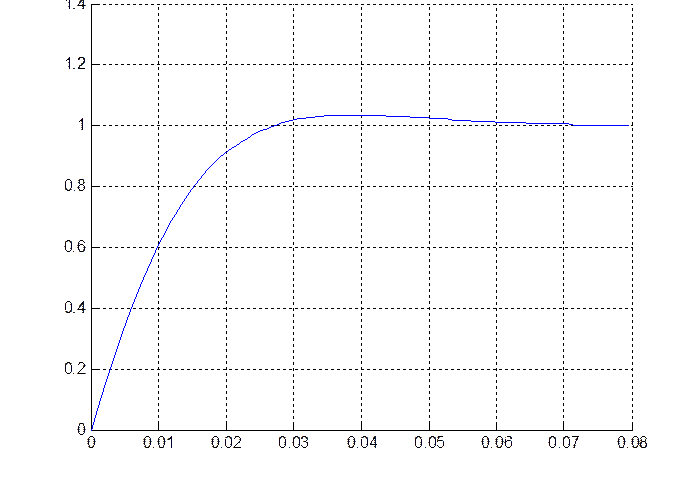
Рис.4.3. Переходная характеристика на выходе инерционного пропорционально дифференцирующего звена при ступенчатом входном воздействии (для третьей точки – t3).

Текущие значения параметров системы:

a1 = 0.008636

a2 = 0.013716

Значение степени устойчивости: 74.231975

Значение степени колебательности: 0.766607

Величина перерегулирования: 4 %

Время переходного процесса: 0.025 с

Амплитуда

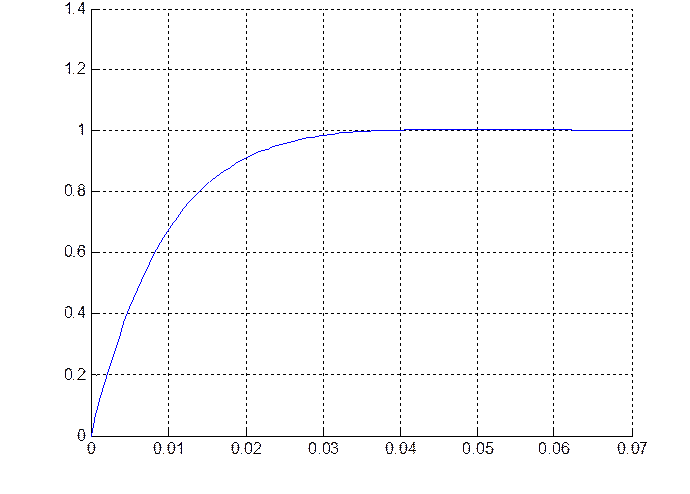 t,c

Рис.4.4. Переходная характеристика на выходе инерционного пропорционально дифференцирующего звена при ступенчатом входном воздействии (для четвертой точки – t4).

Текущие значения параметров системы:

a1 = 0.012056

a2 = 0.013716

Значение степени устойчивости: 89.189164

Значение степени колебательности: 0.315948

Величина перерегулирования: 1 %

Время переходного процесса: 0.025 с

Амплитуда

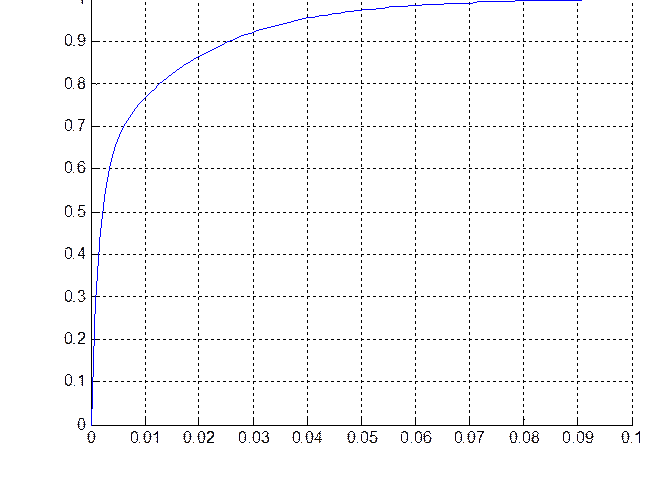 t,c

Рис.4.5. Переходная характеристика на выходе инерционного пропорционально дифференцирующего звена при ступенчатом входном воздействии (для пятой точки – t5).