Исследование устойчивости разомкнутой и замкнутой системы. Необходимое и достаточное условие устойчивости, страница 2

Текущие значения параметров системы:

a1 = 0.012056

a2 = 0.013716

Значение степени устойчивости: 89.189164

Значение степени колебательности: 0.315948

Величина перерегулирования: 0 %

Время переходного процесса: 0.04 с

Амплитуда

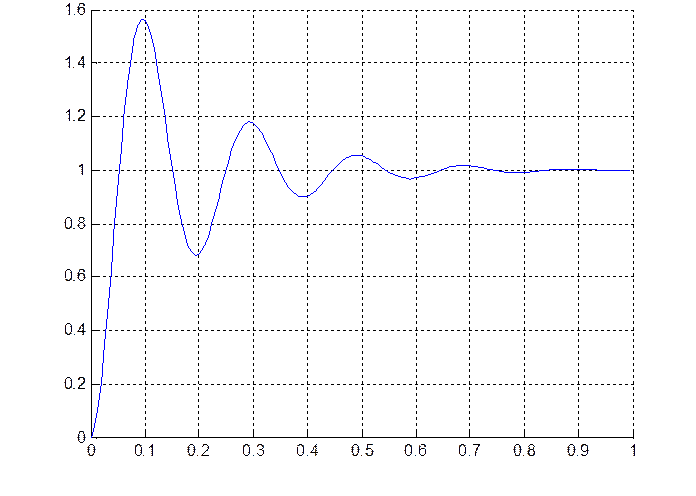 t,c

Рис.4.6. Переходная характеристика на выходе инерционного пропорционально дифференцирующего звена при ступенчатом входном воздействии (для шестой точки – t6).

Текущие значения параметров системы:

a1 = 0.002748

a2 = 0.114163

Значение степени устойчивости: 5.823782

Значение степени колебательности: 5.476482

Величина перерегулирования: 55 %

Время переходного процесса: 0.05 с

Первая точка (t1) является оптимальной по условиям качества переходного процесса:

k1 = 0.010141 с

T0 = 0.010125 с

Чувствительность системы к изменению параметров:

По степени устойчивости: при изменении параметров на 20% степень устойчивость изменяется на 19%.

По степени колебательности: при изменении параметров на 20% степень колебательности изменяется на достаточно малую величину (процентное сравнение невозможно в связи с номинальным значением колебательности 0).

5. Построение фазового портрета нелинейной системы, считая регулятор безынерционным звеном и полагая W_p(p)=1. Сделать выводы об устойчивости и характере процессов в системе. Построить примерный вид переходного процесса по фазовым траекториям для характерных начальных условий.

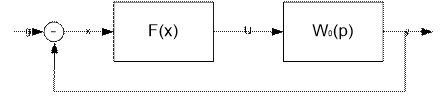
Рис.5.1. Структурная схема системы

  -  передаточная характеристика нелинейного элемента   

Рис. 5.2. Передаточная характеристика трехпозиционного реле с гистерезисом.

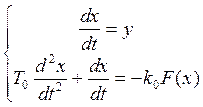
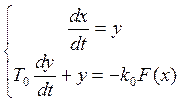
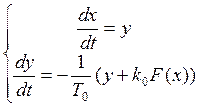
Рис. 5.3. Фазовый портрет нелинейной системы второго порядка.

Рис. 5.4. Переходный процесс.

6. Промоделировать нелинейную систему 2-го порядка в Simulink. Сравнить фазовые портреты, полученные расчетным способом с результатами моделирования. Ввести обратную связь по скорости и исследовать ее влияние на процессы в системе.

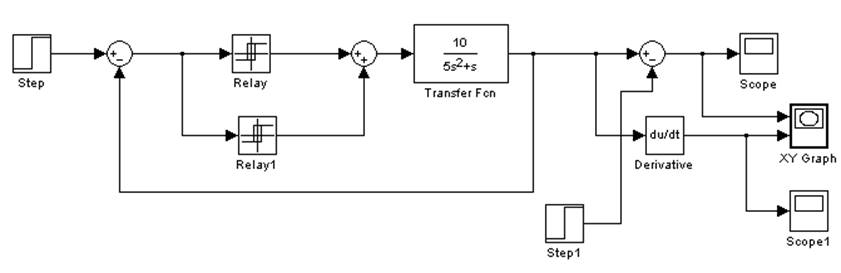
Рис. 6.1. Структурная схема нелинейной САУ в Simulink.

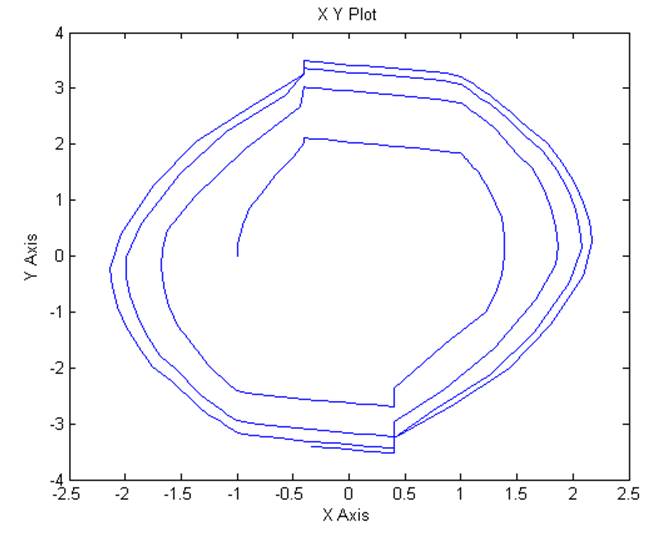
Рис. 6.2. Фазовый портрет нелинейной системы второго порядка.

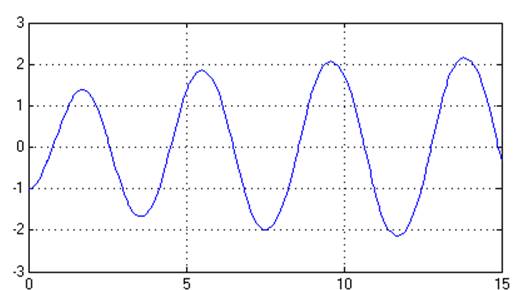
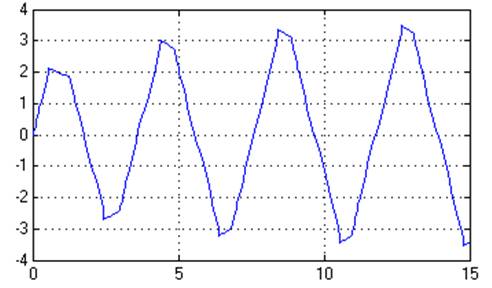
Рис. 6.3. Переходный процесс.

Можно пронаблюдать сходство фазовых портретов, полученных расчетным способом и полученных в результате моделирования.

Введем обратную связь по скорости в исследуемой системе.

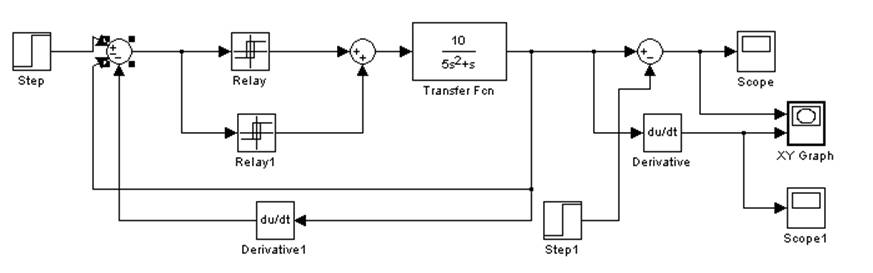
Рис. 6.4. Структурная схема нелинейной САУ с обратной связью по скорости в Simulink (1 вариант).

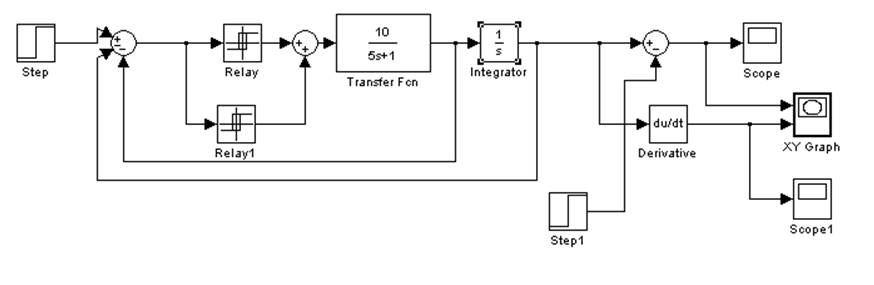
Рис. 6.5. Структурная схема нелинейной САУ с обратной связью по скорости в Simulink (2 вариант).

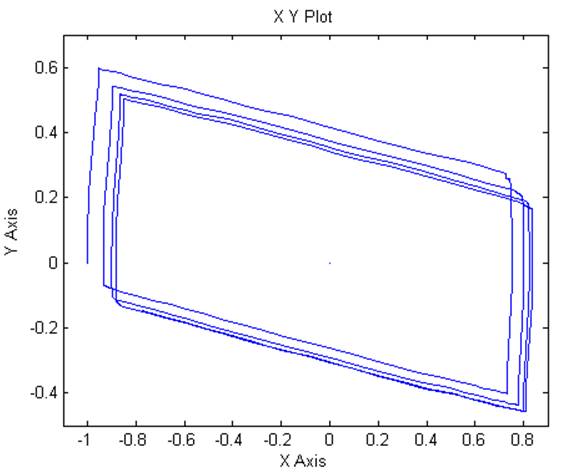
Рис. 6.6. Фазовый портрет нелинейной системы второго порядка с обратной связью по скорости (смещение нулевое).

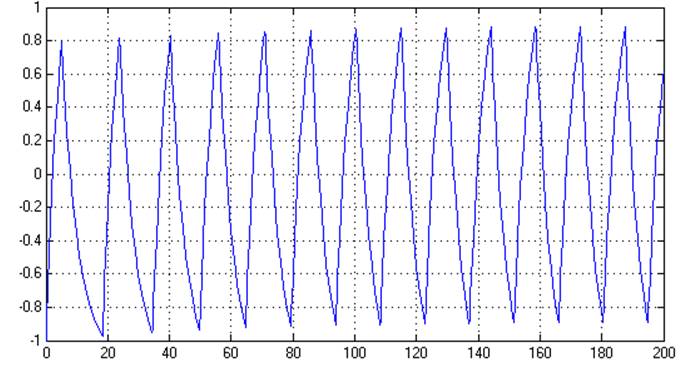
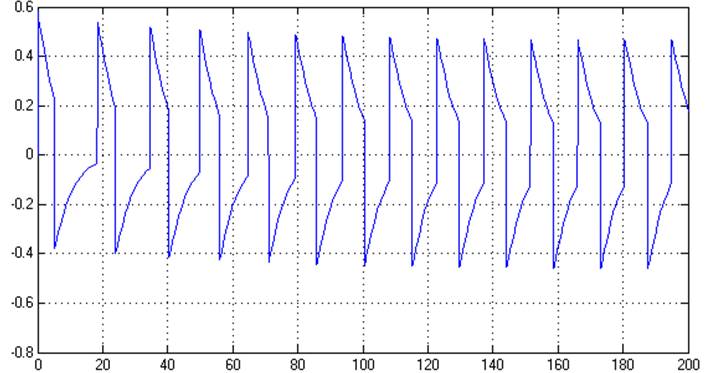
Рис. 6.7. Переходный процесс.

Установим в свойствах интегратора Исходное условие -1.

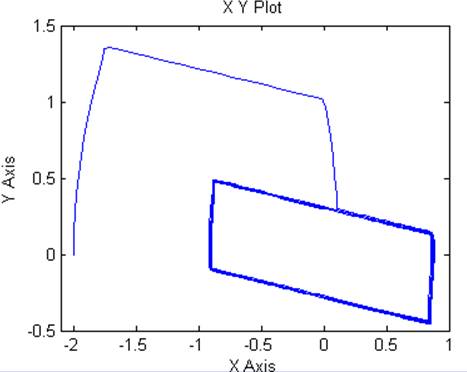
Рис. 6.8. Фазовый портрет нелинейной системы второго порядка с обратной связью по скорости.

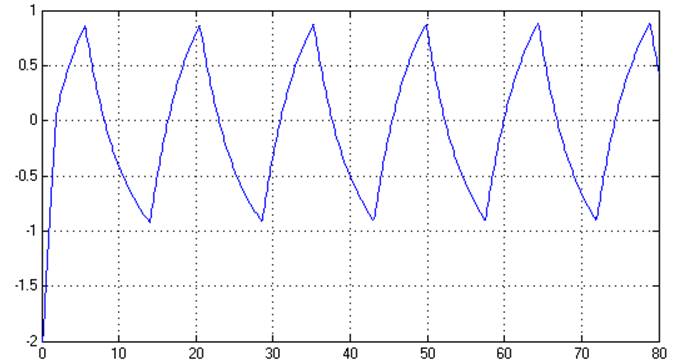
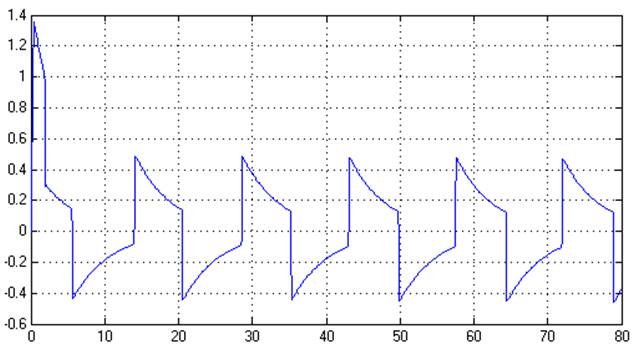
Рис. 6.9. Переходный процесс.

Установим в свойствах интегратора Исходное условие -5.

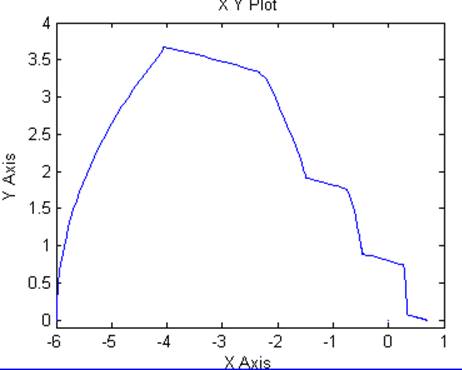
Рис. 6.10. Фазовый портрет нелинейной системы второго порядка с обратной связью по скорости.

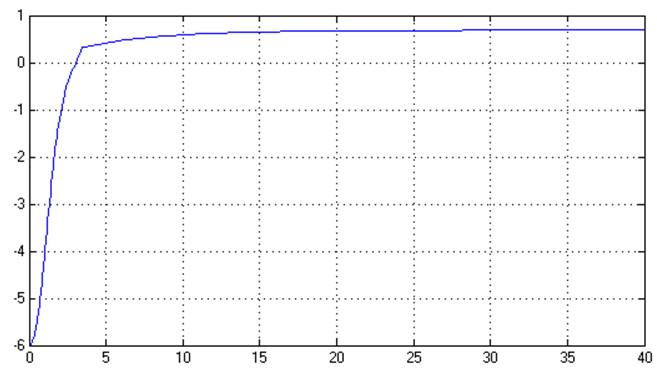
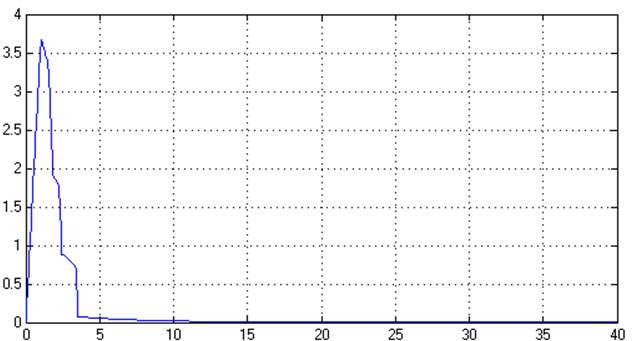
Рис. 6.11. Переходный процесс.

7. Исследование автоколебаний при включении в систему на входе регулятора нелинейного звена. Исследование условий возникновения автоколебаний (найти Tгр). Построить зависимости амплитуды и частоты автоколебаний от T0.

Передаточная функция линейной системы:

Передаточная функция нелинейного звена:

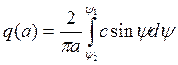
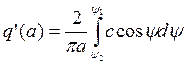
Характеристическое уравнение замкнутой системы:

Выделим в данном уравнении вещественную и мнимую часть:

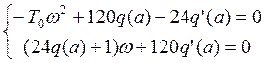
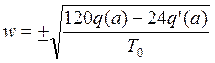- частота автоколебаний больше нуля, следовательно:;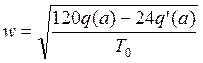

Область допустимых значений .

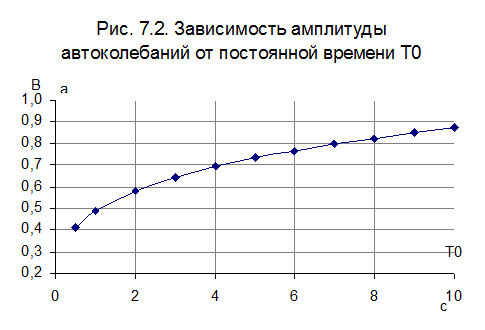
Зависимости амплитуды и частоты автоколебаний на выходе САУ от постоянной времени T0.

Таблица 7.1

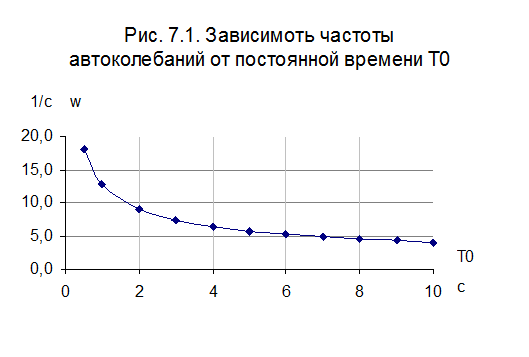
Таблица 7.2