Изучение методов дискретного описания непрерывных звеньев. Добавление анимации в созданную ранее в соответствии с индивидуальным заданием сцену

Санкт-Петербургский государственный политехнический университет

Факультет технической кибернетики

Кафедра компьютерных систем и программных технологий

Отчет по лабораторной работе №13

(Учебная дисциплина «Теория автоматического управления»)

Изучение методов дискретного описания

непрерывных звеньев

Работу выполнил студент группы №4081/2                     

Работу принял преподаватель___________                                 В

Санкт-Петербург

2010

1. Цель работы.

Изучение методов получения дискретной передаточной функции непрерывной части цифровой системы.

2. Способы вычисления дискретной передаточной функции.

Точным способом дискретная передаточная функция W(z) непрерывной части системы с идеальным ключом и фиксатором на входе определяется следующим образом.

 

Обычно используют разложение на простые типовые слагаемые, Z-преобразования которых находят с помощью таблиц преобразований типовых функций.

Приближенным способом W(z) определяется путем замены оператора p в выражении непрерывной передаточной функции на оператор дифференцирования выбранного конечно-разностного алгоритма (T – период дискретизации):

•  - метод прямых разностей (метод Эйлера);

•  - метод обратных разностей (метод Эйлера);

•  - метод трапеций (преобразование Тастина).

3. Выполнение работы.

3.1. Звено 1.

Дискретная передаточная функция, найденная точным способом:

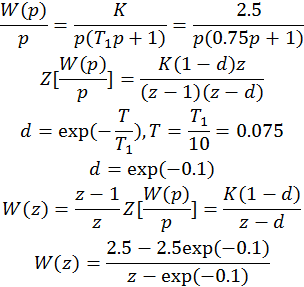
Схема моделирования в Simulink.

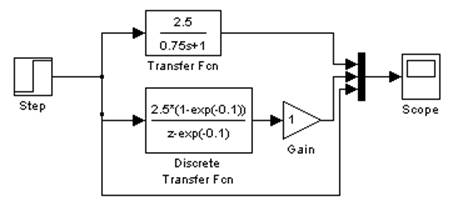
Рис. 3.1.1. Схема моделирования в Simulink. Точный способ.

В источнике сигнала Step выставим период дискретизации кратный периоду квантования , возьмем его равным 0.075.

Усилитель на выходе необходим для установки периода дискретизации, чтобы сравнивать сигналы на выходе непрерывной и дискретной системы в разных точках (не только в точках с дискретизации системы).

Снятая осциллограмма:      

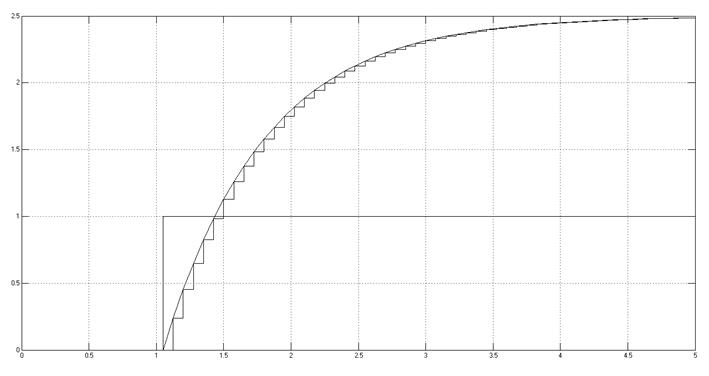
Рис. 3.1.2. Снятая осциллограмма. Точный способ.

Дискретные передаточные функции полученные приближенными методами, схемы моделирования и снятые осциллограммы.

Метод прямых разностей Эйлера.

Дискретная передаточная функция.

Схема моделирования в Simulink.

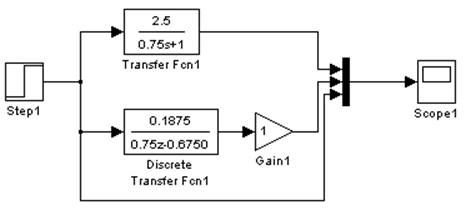
Рис. 3.1.3. Схема моделирования в Simulink. Метод Эйлера.

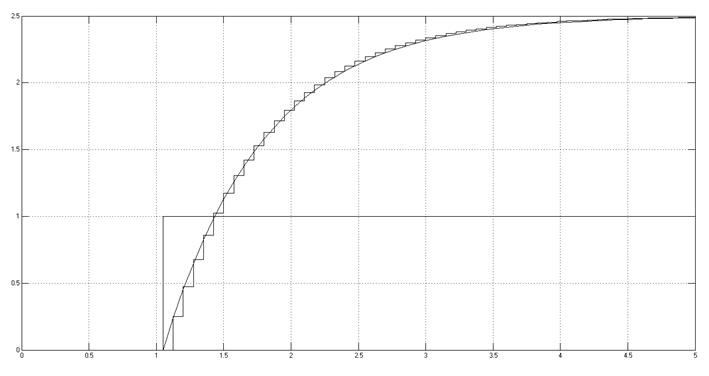
Рис. 3.1.4. Снятая осциллограмма. Метод Эйлера.

Метод Тастина.

Дискретная передаточная функция.

Схема моделирования в Simulink.

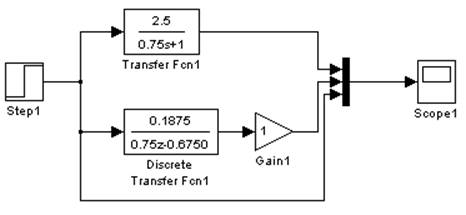
Рис. 3.1.5. Схема моделирования в Simulink. Метод Тастина.

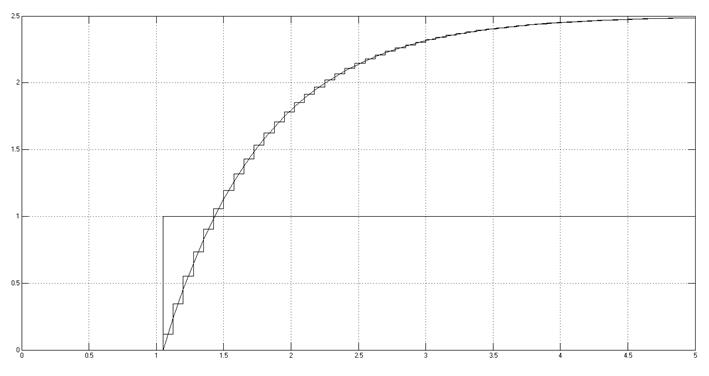
Рис. 3.1.6. Снятая осциллограмма. Метод Тастина.

Сравним методы получения дискретной передаточной функции.

Найдем ошибку в точках дискретизации. Для этого выведем полученные данные с осциллограмм в Workspace Matlab. Чтобы искать погрешность только в точках дискретизации (Т = 0.075)  установим в Sample Time усилителя на выходе дискретной передаточной функции время равное периоду квантования, с которым рассчитана ДПФ. Ищем ошибку как среднеквадратическую от разности непрерывной ПФ и дискретной ПФ в интересующих нас точках (функция mse в Matlab).

Результаты:

•  Точный метод — 2.0832e-018;

•  Метод Эйлера — 5.1230e-004;

•  Метод Тастина — 9.7990e-004.

Теперь рассмотрим ошибку не только в точках дискретизации точной ДПФ. Для этого зададим период квантования в выходном усилителе равный, например, 1e-4.

Результаты:

•  Точный метод — 0.0013;

•  Метод Эйлера — 8.6800e-004;

•  Метод Тастина — 3.2535e-004.

Выводы:

Из результатов можно сделать следующие выводы. Точный метод дает очень маленькую ошибку только в точках дискретизации для которых и была рассчитана точная ДПФ, а если брать в расчет и промежуточные точки, то точный метод дает большую среднюю ошибку.

Приближенные методы дают ошибку одинакового порядка в обоих случаях. Для промежуточных точек самую маленькую среднюю ошибку имеет метод Тастина.

3.1. Звено 2.

Дискретная передаточная функция, найденная точным способом:

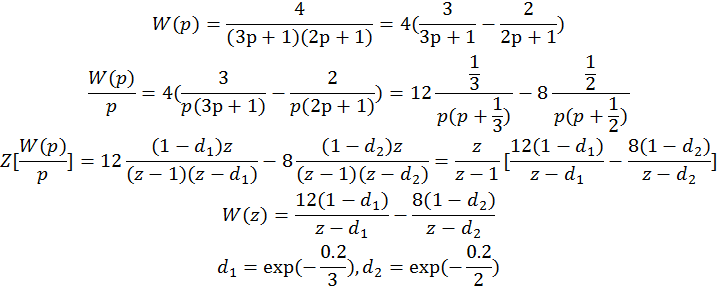
Период дискретизации взят равным 0.1 самой маленькой постоянной времени.

Схема моделирования в Simulink.

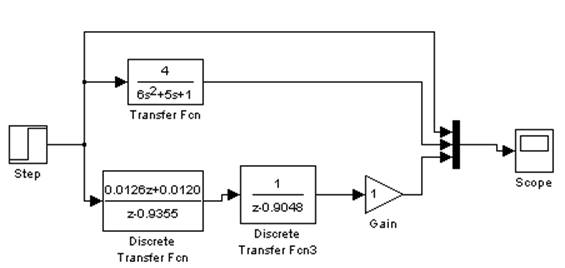
Рис. 3.2.1. Схема моделирования в Simulink. Точный метод.

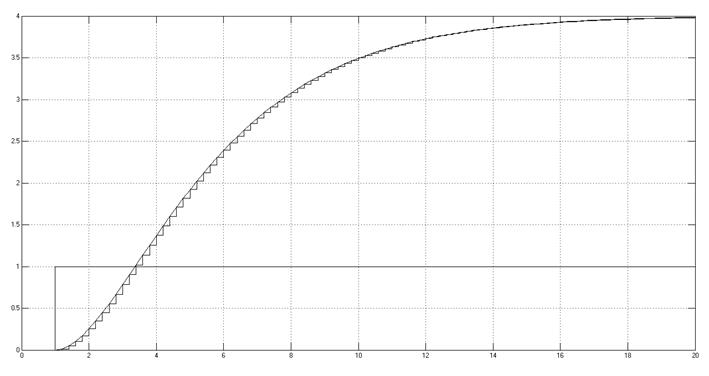
Рис. 3.2.2. Снятая осциллограмма. Точный метод.

Метод прямых разностей Эйлера.

Дискретная передаточная функция.

Схема моделирования в Simulink.

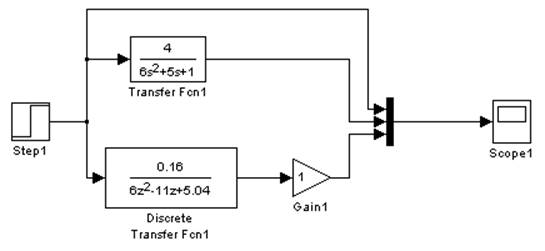
Рис. 3.2.3. Схема моделирования в Simulink. Метод Эйлера.

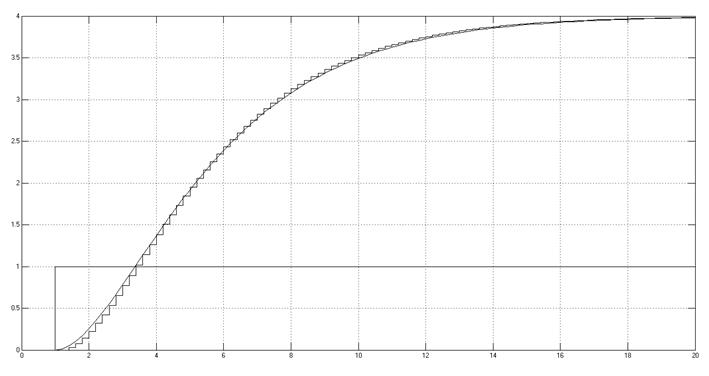
Рис. 3.2.4. Снятая осциллограмма. Метод Эйлера.

Метод Тастина.

Дискретная передаточная функция.

Схема моделирования в Simulink.

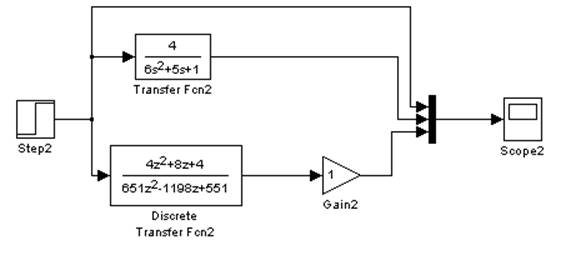
Рис. 3.2.5. Схема моделирования в Simulink. Метод Тастина.

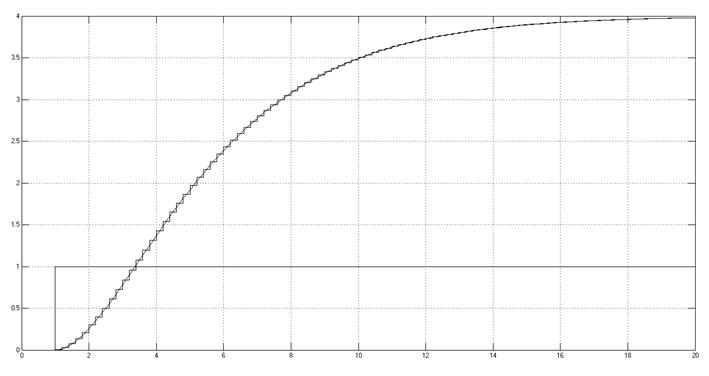
Рис. 3.2.6. Снятая осциллограмма. Метод Тастина.

Сравним методы получения дискретной передаточной функции. Ошибку, как и для 1го звена считаем в двух случаях.

Только в точках дискретизации точной ДПФ.

Результаты:

•  Точный метод — 1.0639e-017;

•  Метод Эйлера — 8.1954e-004;

•  Метод Тастина — 7.8120e-004.

Теперь рассмотрим ошибку не только в точках дискретизации точной ДПФ. Для этого зададим период квантования в выходном усилителе равный, например, 1e-4.

Результаты:

•  Точный метод — 0.0011;

•  Метод Эйлера — 0.0011;

•  Метод Тастина — 2.6673e-004.

Выводы:

Как и для предыдущего звена точный метод дает очень маленькую ошибку только в точках дискретизации для которых и была рассчитана точная ДПФ, а если брать в расчет и промежуточные точки, то точный метод дает большую среднюю ошибку.

Для промежуточных точек самую маленькую среднюю ошибку имеет метод Тастина.