1) передаточная функция разомкнутой системы:
![]()
2) статическая характеристика нелинейного элемента (рис.1.1)
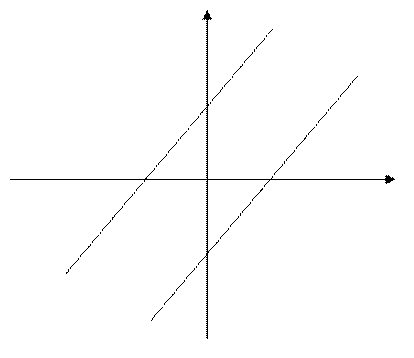
Рис.1.1. Характеристика нелинейного элемента
Пункты задания:
1. исследование линейной системы
Схема линейной системы приведена на рис.1.2.
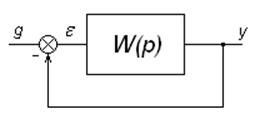
Рис.1.2. Схема линейной системы
1.1. определение устойчивости замкнутой системы
1.2. построение области устойчивости в пространстве двух параметров
1.3. построение линий равной степени устойчивости в области устойчивости
1.4. построение ЛАХ разомкнутой системы
1.5. синтез корректирующих звеньев по заданным динамическим требованиям (получить требования к переходному процессу у преподавателя)
1.6. проверка синтеза и построение переходного процесса
2. исследование нелинейной системы
Схема нелинейной системы приведена на рис.1.3.
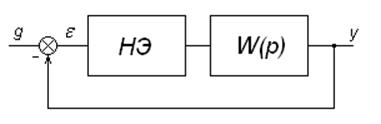
Рис.1.3. Схема нелинейной системы
2.1. определение существования автоколебаний
2.2. частота и устойчивость автоколебаний
2.3. частота и амплитуда автоколебаний
2.4. определение зависимости автоколебаний от варьируемых параметров
Преобразование в полиномиальный вид:
>> num = conv( [100], [1 2.5 1]);
>> den = conv( [1 4 3 0], [0.06 0.7 1]);
>> wp = tf(num, den)
Transfer function:
100 s^2 + 250 s + 100
---------------------------------------------0.06 s^5 + 0.94 s^4 + 3.98 s^3 + 6.1 s^2 + 3 s
Для этого воспользуемся алгебраическим критерием.
>> wpos = feedback(wp, 1)
Transfer function:
100 s^2 + 250 s + 100
-------------------------------------------------------0.06 s^5 + 0.94 s^4 + 3.98 s^3 + 106.1 s^2 + 253 s + 100
>> pole(wpos)
ans =
-17.03366513147392
1.93318403936321 + 9.72363589813767i
1.93318403936321 - 9.72363589813767i
-2.00214571361885
-0.49722390030029
Замкнутая система неустойчива, т.к. у ее передаточной функции есть полюса с положительной вещественной частью.
>> wpsym = K*(p^2+T*p+1)/(p^3+4*p^2+3*p)/(0.06*p^2+0.7*p+1);
>> pretty(wpsym)
2
K (p + T p + 1)
---------------------------------------3 2 2
(p + 4 p + 3 p) (3/50 p + 7/10 p + 1)
>> wpsymos = wpsym/(wpsym+1);
>> simplify(wpsymos);
>> collect(ans)
ans =
50*K*(p^2+T*p+1)/(3*p^5+47*p^4+199*p^3+(50*K+305)*p^2+(50*K*T+150)*p+50*K)
>> pretty(ans)
2
K (p + T p + 1)
50 ----------------------------------------------------------------5 4 3 2
3 p + 47 p + 199 p + (50 K + 305) p + (50 K T + 150) p + 50 K
Т.о имеем характеристический полином с коэффициентами:
>> dcom('[0.06, 0.94, 3.98, y+6.1, y*x+3, y]', -40:0.1:40, -30:0.1:50)
>> stabreg('[0.06, 0.94, 3.98, y+6.1, y*x+3, y]', -40:0.5:40, -30:0.5:50)
Области устойчивости в пространстве параметров T и K представлены на рисунке 2.1 и результат D-разложения на рисунке 2.2.
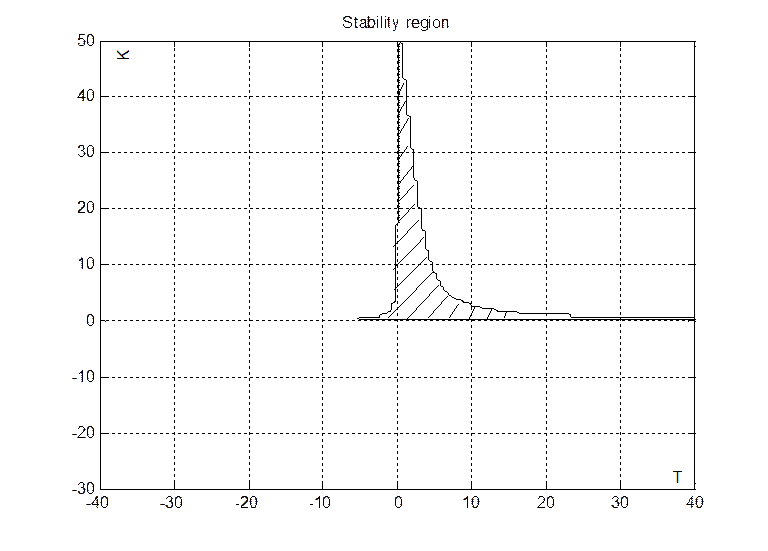
Рис.2.1. Области устойчивости
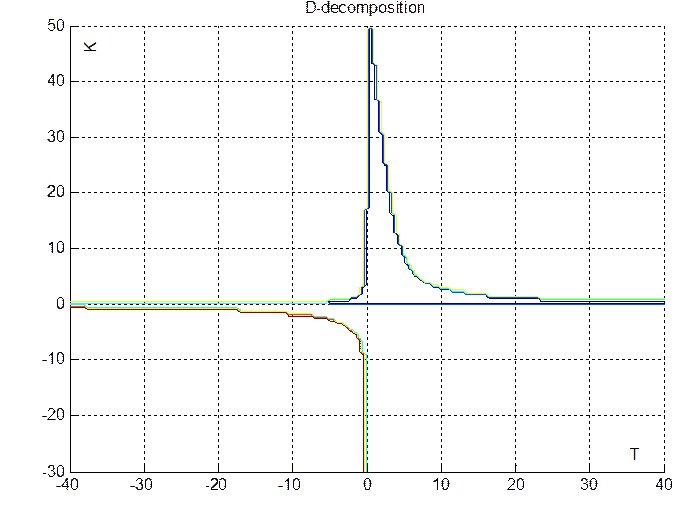
Рис.2.2. D-разбиение
Проверка результатов построения. Зададимся параметрами K T, входящими в область устойчивости, например K = 5, T = 10:
>> num1 = conv( [5], [1 2 1]);
>> wp1 = tf(num1, den)
Transfer function:
5 s^2 + 10 s + 5
---------------------------------------------0.06 s^5 + 0.94 s^4 + 3.98 s^3 + 6.1 s^2 + 3 s
>> wp1os = feedback(wp1, 1)
Transfer function:
5 s^2 + 10 s + 5
---------------------------------------------------0.06 s^5 + 0.94 s^4 + 3.98 s^3 + 11.1 s^2 + 13 s + 5
>> pole(wp1os)
ans =
-11.01191850637965
-1.41006814673881 + 2.66061390833795i
-1.41006814673881 - 2.66061390833795i
-1.00000000000001
-0.83461186680939
Что и требовалось доказать. Для прочих областей D-разбиения проверка аналогична.
R = [k, t*k, k];
Q = [0.06, 0.94, 3.98, k+6.1, k*t+3, k];
rtanalti('my_data')
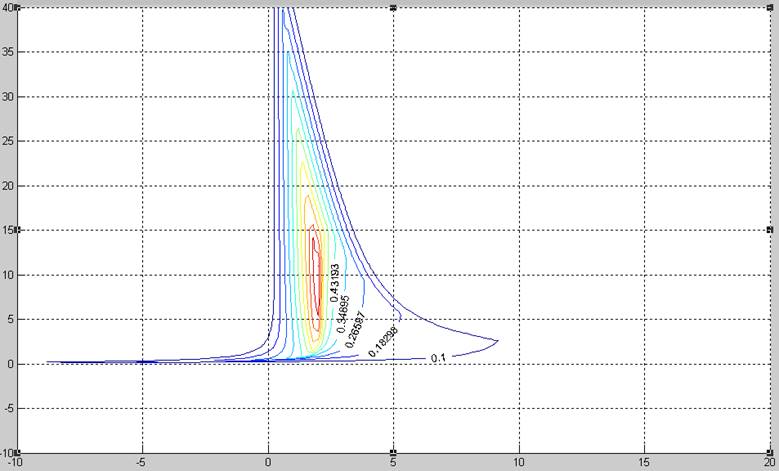
Рис 2.3. Линии равной степени устойчивости
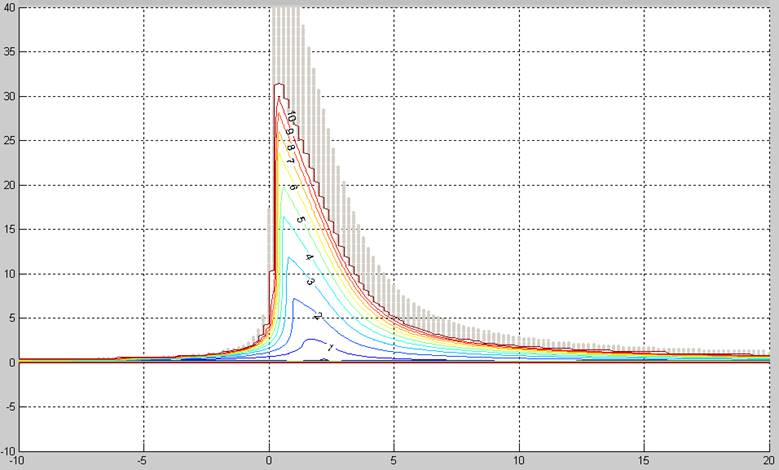
Рис 2.4. Линии равной степени колебательности
![]()
>> num = conv( [100], [1 2.5 1]);
>> den = conv( [1 4 3 0], [0.06 0.7 1]);
>> wp = tf(num, den)
Transfer function:
100 s^2 + 250 s + 100
---------------------------------------------0.06 s^5 + 0.94 s^4 + 3.98 s^3 + 6.1 s^2 + 3 s
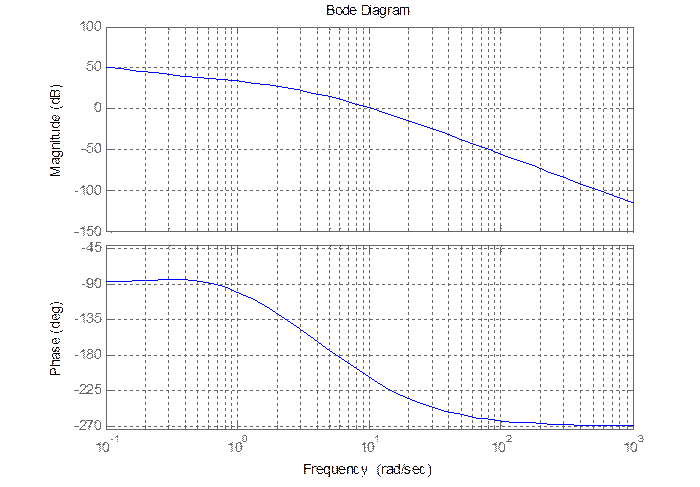
Рис.2.5. Логарифмические характеристики разомкнутой системы
Заданные параметры качества переходного процесса:
время переходного процесса ![]() и
перерегулирование
и
перерегулирование ![]() .
.
Схема САР с корректирующем звеном представлена на рисунке 2.6.
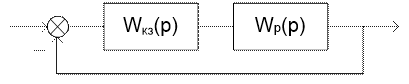
Рис.2.6. Последовательное корректирующее звено
Для синтеза корректирующего звена воспользуемся частотным методом синтеза. Построим ЛАЧХ разомкнутой системы, желаемую ЛАЧХ и получим передаточную функцию корректирующего звена путем алгебраического сложения графиков ЛАЧХ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.