Санкт–Петербургский Государственный Политехнический Университет
Факультет Технической Кибернетики
Кафедра Автоматики и Вычислительной Техники
ОТЧЕТ
О лабораторной работе
Дисциплина: ТАУ
Тема: Математические модели систем
Выполнил студент группы 3081/1
Руководитель:
Санкт-Петербург
2009
Изучение способов математического описания и методов структурного моделирования систем управления.
Исходная система имеет передаточную функцию вида:
![]()
Составим матрицы А, B, C и D для заданной системы и проверим управляемость
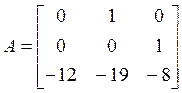 ;
;
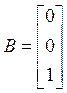 ;
; ![]() ; D = 0;
; D = 0;
Полученная система имеет вид:
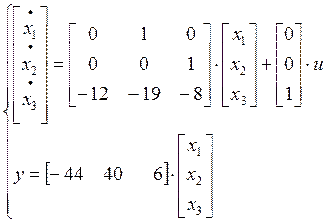
Матрица управляемости имеет
вид ![]() , или подставив значения, получим:
, или подставив значения, получим:
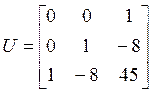 ; rang(U) = 3, что равняется n => система
полностью управляема.
; rang(U) = 3, что равняется n => система
полностью управляема.
Код matlab.
>> A = [0 1 0;0 0 1;-12 -19 -8];
>> B = [0;0;1];
>> C = [-44 40 6];
>> D=0;
>> sys = ss(A,B,C,D);
>> tf(sys)
Transfer function:
6 s^2 + 40 s - 44
-----------------------
s^3 + 8 s^2 + 19 s + 12
>> c0=ctrb(sys)
c0 =
0 0 1
0 1 -8
1 -8 45
>> rank(c0)
ans = 3
Выводы:
Система полностью управляема, о чем говорит совпадение ранга матрицы С с кол-вом элементов n, которое в данном случае равняется трем (следует из старшей степени полинома в знаменателе). Вышеприведенный расчет был осуществлен вручную и так же, в системе matlab, что позволяет говорить о хорошей точности приведенного результата (т.к. все совпало).
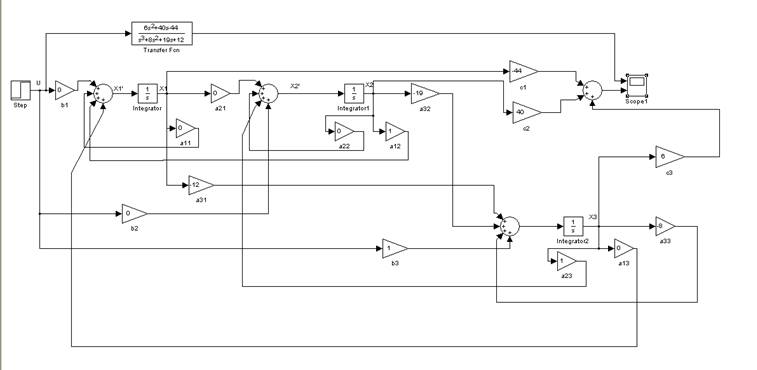
Рис. 3.1. Схема моделирования в приложении simulink
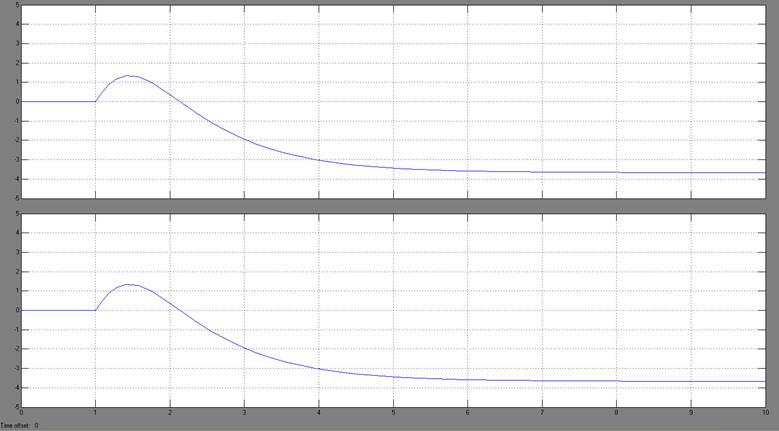
Рис. 3.2. Результаты моделирования
Выводы:
Как видно из полученных результатов, оба сигнала совпали, что говорит об отсутствии погрешности в данном случае при представлении программой Matlab систем в различных описаниях.
Исходная система имеет передаточную функцию вида:
![]()
Составим матрицы А, B, C и D для заданной системы
![]() ;
;
![]() ;
; ![]() ; D = 0;
; D = 0;
Представим матрицу А в диагональной форме:
![]()
Корни этого уравнения:
![]()
![]()
Для определения собственного
вектора, соответствующему числу ![]() , решим систему:
, решим систему:
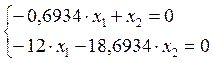 ;
;
Примем ![]() =1, тогда
=1, тогда ![]() =0,6934
=0,6934
Определим собственный вектор,
соответствующий числу ![]() :
:
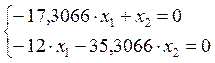 ;
;
Примем ![]() =1, тогда
=1, тогда ![]() =17,3066
=17,3066
Таким образом, получим собственные векторы исходной матрицы А.
![]() ;
;
Тогда матрицу перехода можно найти следующим образом:
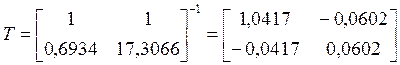 ;
;
Нетрудно проверить: ![]() ;
;
Найдем матрицы ![]() ,
, ![]() и
и
![]() .
.
![]() ;
; ![]() ;
;
Код matlab
>> A=[0 1;-12 18];
>>B=[0;1];
>>C=[-12 8];
>>D=0;
>> A1 = eig(A)
A1 =
0.6934
17.3066
>>A2 = [A1(1) 0;0 A1(2)]
A2 =
0.6934 0
0 17.3066
>> [x2] = solve('-0.6934+x2=0');
>> [x2] = solve('-17.3066+x2=0');
>> T11=[1 1;0.6934 17.3060];
>>T=T11^(-1);
T11 =
1.0000 1.0000
0.6934 17.3060
>> T*A*T11
ans =
0.6934 0.0000
0.0000 17.3066
>> B1=T*B
B1 =
-0.0602
0.0602
>> C=C*T^-1
C = 10.6934
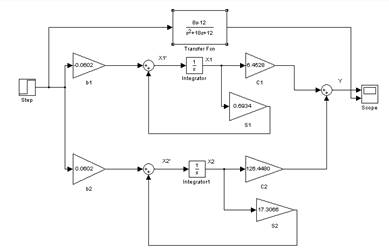
Рис. 5.1. Схема данной системы
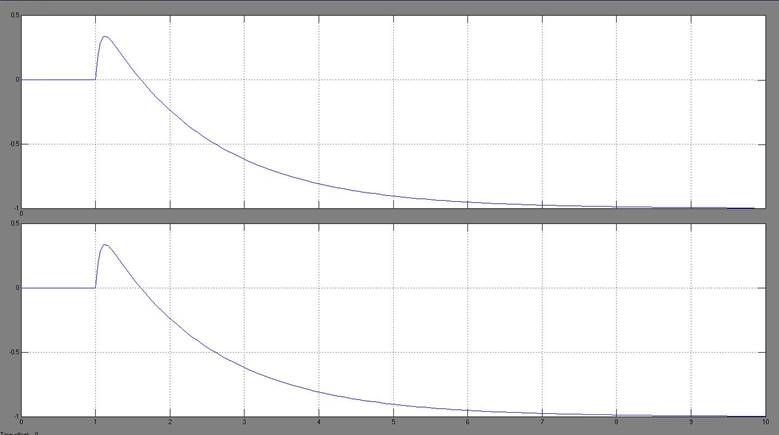
Рис. 5.2. Результаты моделирования полученной схемы
Выводы:
Выходные сигналы в обоих случаях идеально совпали, о чем свидетельствует приведенная выше диаграмма.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.