Структурная схема исследуемой САУ. Передаточная нелинейного элемента типа зазор, люфт. Характеристика нелинейного элемента, страница 2

С помощью программы asymp  в matlab построим ЛАХ разомкнутой системы.

Для этого введём следующие команды:

Передаточная функция:

7500 s + 18750

-------------------------10 s^3 + 51 s^2 + 65 s + 6

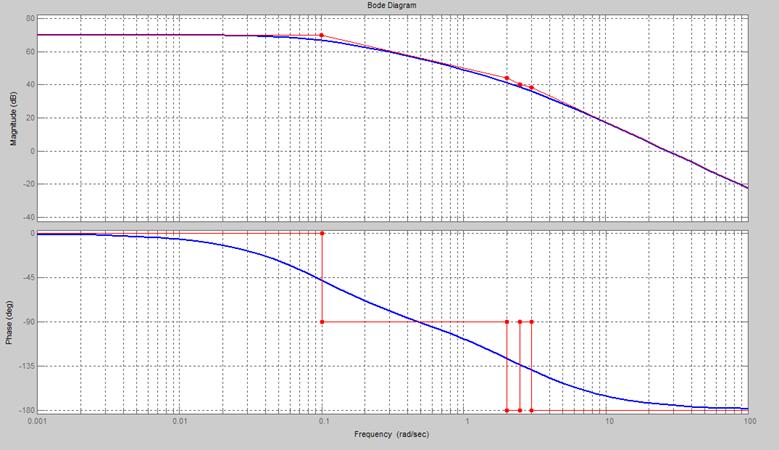
Рис. 4.1. ЛАХ разомкнутой системы.

Необходимо подобрать корректирующее звено к замкнутой системе, чтобы время переходного процесса равнялось 1с, а перерегулирование было не более 35%.

Построим желаемую ЛАХ. Частота среза определяется по формуле

В нашем случае = 4.2, =1, подставляя в формулу получаем

Границы среднечастотной асимптоты выберем из соотношений:

Сопряжение среднечастотной асимптоты с низкочастотной и высокочастотной проведём прямой с наклоном  -40дБ/дек.

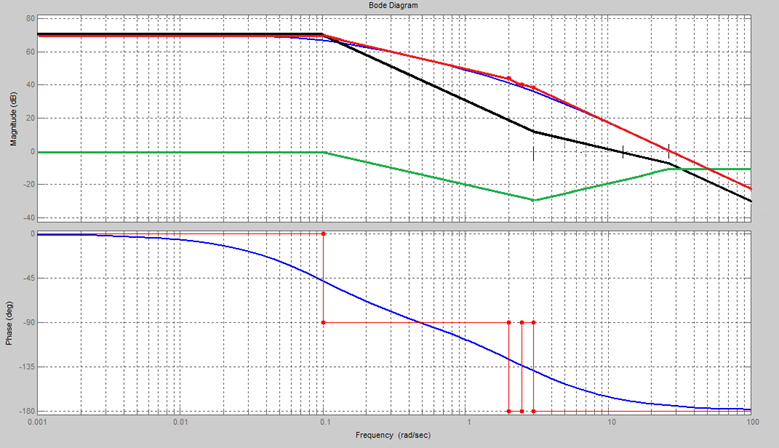
Рис.4.2. построение желаемой ЛАХ и ЛАХ корректирующего звена.

Красная – ЛАХ разомкнутой системы

Чёрная – желаемая ЛАХ

Зелёная – ЛАХ корректирующего звена. Разность между желаемой ЛАХ и ЛАХ разомкнутой системы

Исходя из этого графика построим передаточную функцию корректирующего звена.

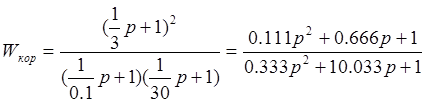
Для проверки соберём схему в simulink.

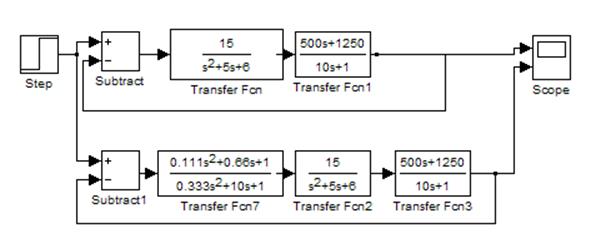
Рис. 4.3 Схема соединения с корректирующим звеном и без него

Графики переходного процесса системы с корректирующим звеном и без него приведены на рисунке.

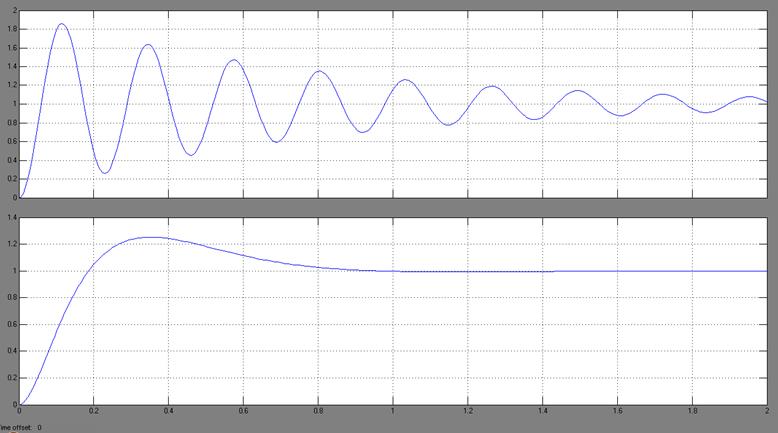
Рис. 4.4. Переходный процесс без корректирующего звена и с ним.

Как видно из графика, время переходного процесса составляет примерно 1с, перерегулирование – 25%. То есть система удовлетворяет поставленным требованиям.

5.  Определение автоколебаний в системе с нелинейным звеном.

Для нелинейности типа люфт по справочнику имеем следующие коэффициенты гармонической линеаризации для данного типа нелинейности:

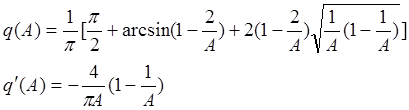
В системе имеются автоколебания, если выполняется условие

Подставим значения в это выражение и посмотрим, существуют ли положительные вещественные значения амплитуды и частоты автоколебаний.

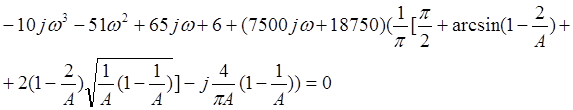
Объединяя вещественную и мнимую часть и приравнивая обе части к нулю получаем систему:

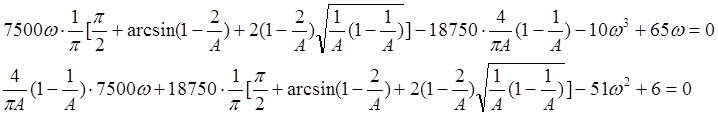
Занося данную систему в matlab с помощью команды solve находим решения.

[A,w] =solve(7500*w*T-18750*N - 10*w^3 + 65*w, N*7500*w+18750*T-51*w^2+6)

Здесь приняты обозначения:

Т =

N =

Получается единственное решение системы:

A =

12.58514105862608303036894243063655

w =

26.873287221704498827767607118015428

То есть в данной системе существуют автоколебания. Проверим это, собрав в simulink эту систему.

Схема системы приведена на рисунке.

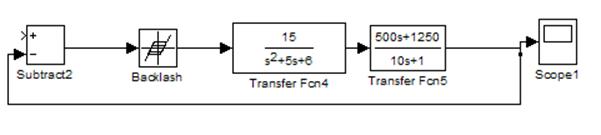
Рис.5.1. Схема с нелинейным звеном.

На рисунке приведён результат моделирования. Амплитуда и частота автоколебаний совпадает с расчётными значениями.

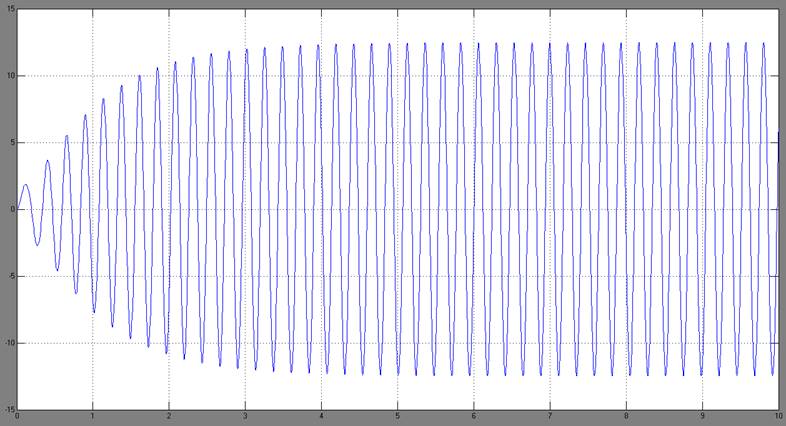
Рис.5.2. Автоколебания.

6.  Определение параметров автоколебаний в системе с нелинейным звеном в зависимости от изменяемых параметров.

Обозначим первый параметр за х, второй за у, и в matlab будем решать систему, изменяя эти параметры.

[A,w] =solve(7500*w*x*T-18750*N - 10*w^3 + 60*w +5*w*y, N*7500*x*w+18750*T-50*w^2-y*w^2+6*y)

В таблицу занесём получившиеся значения амплитуды и частоты и построим соответствующие графики.

Табл. 6.1 Зависимость A и ω от первого параметра

Соответствующие графики приведены на рисунках.

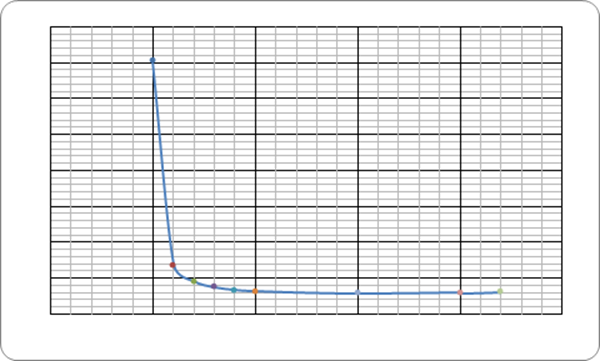
Рис.6.1. Зависимость A(x)

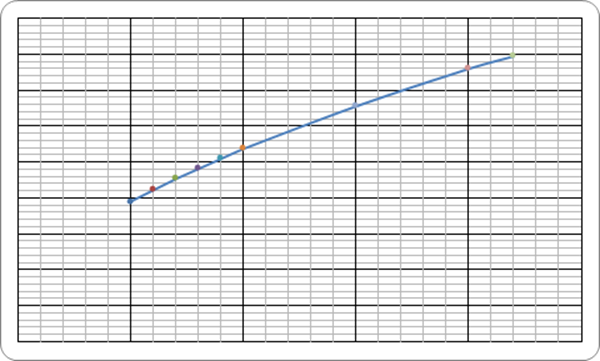
Рис.6.2. Зависимость ω(x)

Табл. 6.2 Зависимость A и ω от второго параметра

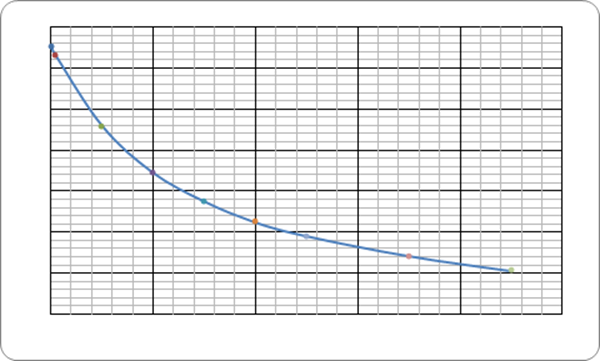
Рис.6.3. Зависимость A(у)

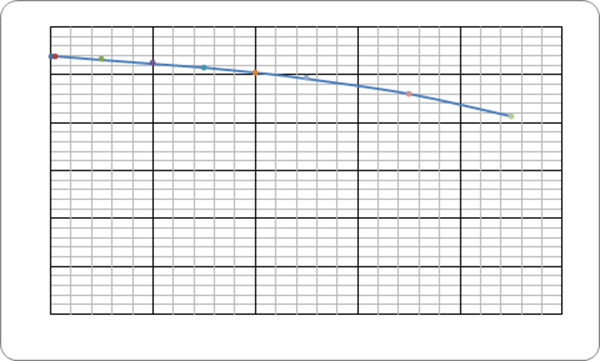
Рис.6.4. Зависимость ω(у)

При дальнейшем изменении параметров x и у в любую сторону в системе перестают происходить автоколебания. При решении соответствующей системы в matlab появляются отрицательные или комплексные значения частоты и амплитуды автоколебаний. Для примера возьмём крайнее значение x=0,5 при y = 1. Результат моделирования этой системы в simulink представлен на рисунке.

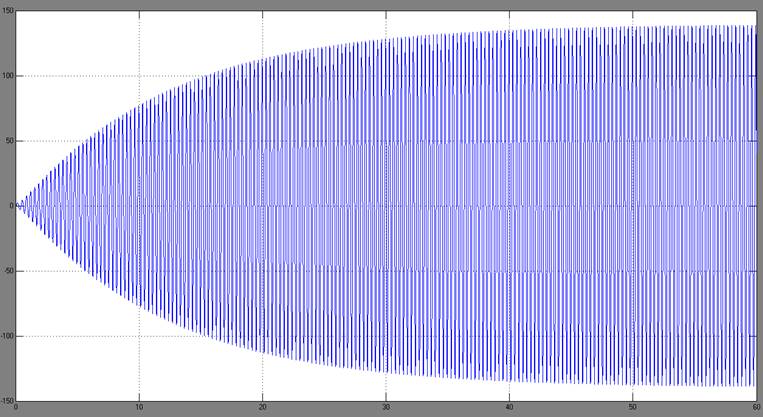
Рис.6.5. Результат моделирования при x=0,5 y=1

При значениях х=0,4 у=1 получаем в решении системы комплексные корни. Результат моделирования при данных параметрах представлен на рисунке.

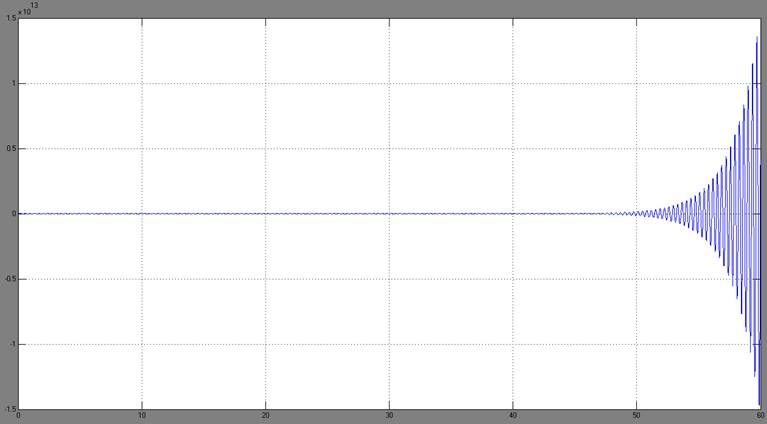
Рис.6.6. Результат моделирования при x=0,4 y=1