Санкт-Петербургский государственный политехнический университет
Факультет технической кибернетики
Кафедра автоматики и вычислительной техники
Дисциплина: компьютерные системы управления
Тема: Исследование оптимальной системы ЛК – управления с наблюдателем Калмана
Выполнил студент гр. 5081/1
Проверил:
Санкт-Петербург
2009
1. Цель работы
Изучение организации, методов синтеза и исследование особенностей работы оптимальной системы линейно-квадратичного управления (ЛК-управления) с наблюдателем Калмана.
2. Теоретические сведения
Как известно, организация систем оптимального терминального управления с интегральным квадратичным критерием качества (системы ЛК - управления) требует знания всех координат состояния объекта управления.
В случае, когда часть из этих координат по каким-либо причинам не измеряемы, реализация ЛК-управления возможна, если в системе производится их восстановление. Известны различные способы построения таких восстановителей, получивших в литературе название наблюдателей. Если объект и измеритель координат находятся под воздействием случайных помех, в качестве наблюдателя наибольшее распространение получил фильтр Калмана.
Следует отметить лишь то, что наблюдатели для восстановления неизмеряемых координат, как правило, используют идею применения адекватной объекту математической модели, в которой доступны для измерения все координаты. Эти координаты и применяются при синтезе оптимального управления. С целью уменьшения влияния задержек, в наблюдателе Калмана реализуются прогнозируемые на такт вперед значения координат состояния объекта.
Так как прогнозируемые и реальные (измеряемые) их значения неизбежно отличаются, в структуру фильтра Калмана включена цепь коррекции прогнозируемого значения координат. Для этой коррекции и используется рассогласование (невязка) между реальными (измеряемыми) и прогнозируемыми координатами состояния .
На рис.2.1 приведена структурная схема системы оптимального терминального
ЛК-управления с фильтром Калмана в качестве наблюдателя. Если сравнить структуру системы ЛК-управления с полностью измеряемыми координатами состояния с системой, показанной на рис. 2.1, можно отметить, что последняя значительно сложнее.
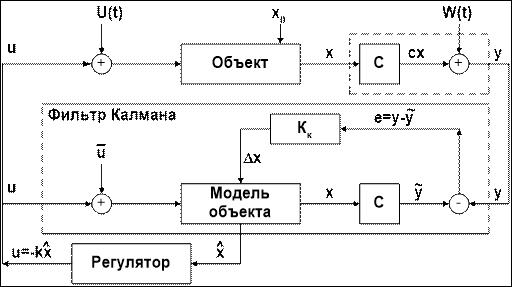
Чтобы оценить эффективность применения наблюдателей, существенно усложняющих структуру управления по сравнению с системой без наблюдателя, в данной работе используется метод экспериментальной оценки сравниваемых систем. При этом следует учитывать, что в системе с наблюдателем (рис. 2.1), помимо задачи восстановления неизмеряемых координат решается так же задача фильтрации помех. В ряде случаев эта задача может быть даже определяющей, т.е. такое сравнение будет не корректно.
Рассмотрим более подробно формализованное описание системы с наблюдателем и применяемые в таких системах обозначения параметров и переменных
Пусть имеется объект, описываемый следующей системой уравнений:
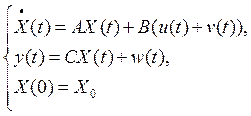 (1)
(1)
где :
x– вектор координат состояния объекта, ![]() ;
;
y – вектор
измеряемых координат, ![]() ;
;
А,В – постоянные матрицы параметров объекта;
С – матрица измерений;
u – сигнал управления;
n, w – векторный «белый шум» (помеха) с характеристиками:
мат. ожидание M( v)= ¯n ; M(w)=¯w и дисперсиями V и W соответственно
Согласно идее построения фильтра Калмана, в структуре последнего должен присутствовать дискретный эквивалент объекта (1), обеспечивающий формирование прогнозируемого значения полного вектора состояния в виде алгебраических уравнений:
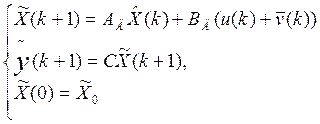 (2)
(2)
где: ![]() - прогнозируемое значение полного
вектора координат;
- прогнозируемое значение полного
вектора координат;
ỹ- прогнозируемое значение измеряемых координат;
![]() - дискретное время, измеряемое в
интервалах квантования Т0;
- дискретное время, измеряемое в
интервалах квантования Т0;
![]() - оценка полного вектора координат
состояния;
- оценка полного вектора координат
состояния;
Ад, Вд - матрицы параметров дискретной модели объекта;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.