Исследование оптимальной системы ЛК – управления с наблюдателем Калмана. Трехмерная система представления модели RGB, страница 3

Критерии оптимальности:        

Время переходного процесса:         

Оптимальные коэффициенты обратной связи:          

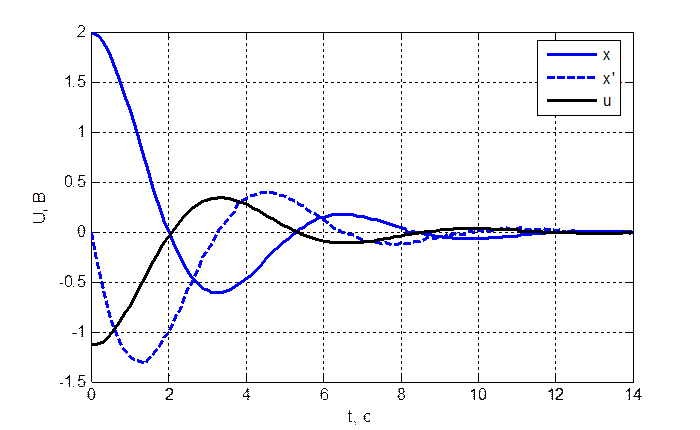
Рис. 3.4.3. Переходный процесс замкнутой системы при

Рис. 3.4.4. Переходный процесс объекта и наблюдателя при .

Критерии оптимальности:        

Время переходного процесса:                       Колебательность:                

При отсутствии управления по выходной координате состояния объекта, ухудшается качество переходного процесса системы - увеличивается время, при этом, отсутвие управления по производной выходной координаты приводит к увеличению колебательности системы, времени переходного процесса.

3.5. Исследование системы ЛК – управления с полностью измеряемыми координатами состоянии объекта при различных начальных условии

Рис. 3.5.1. Переходный процесс системы при .

Рис. 3.5.2. Переходный процесс объекта и наблюдателя при .

Критерии оптимальности:        

Время переходного процесса:         

Колебательность:            

3.6. Исследование системы ЛК - управления при различных матрицах весовых коэффициентов критерия оптимальности Q и R

Первая производная объекта  является неизмеряемой величиной.

Рис. 3.6.1. Переходные процессы системы при различных отношениях Q/R,

.

3.7. Исследование работы системы ЛК – управления с неполностью наблюдаемым вектором состояния с наблюдателем (фильтром Калмана) в условиях помех типа «белый шум»

В данном пункте рассматривается система с использованием фильтра Калмана с неизмеряемой координатой по производной. При этом к полученному выходному сигналу добавляется помеха типа «белый шум».

Оптимальные коэффициенты обратной связи:          

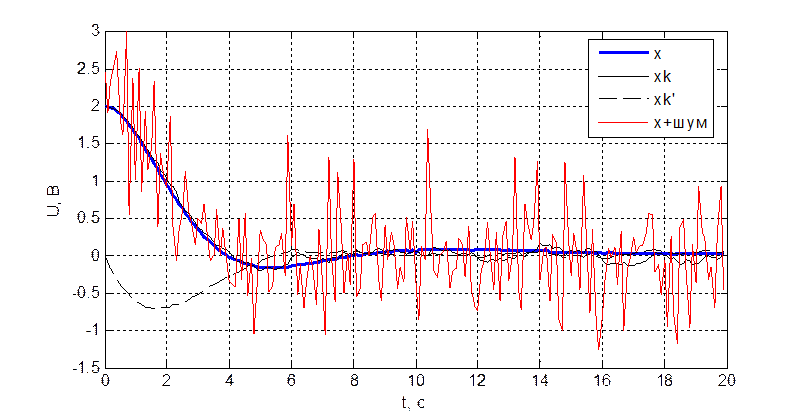
Рис. 3.7.1. Переходный процесс объекта и наблюдателя при .

Оптимальные коэффициенты обратной связи:          

Рис. 3.7.1. Переходный процесс объекта и наблюдателя при .

Рис. 3.7.1. Переходный процесс объекта и наблюдателя при .

В данном случае также происходит получение оптимальной переходной характеристики системы и восстановление ненаблюдаемых координат.

Значение критерия , что практически совпадает с теоретическим.

Погрешность восстановления выходной координаты . Относительная погрешность .

Погрешность восстановления ненаблюдаемой координаты (производной) . Относительная погрешность .

Т.о. при использовании ЛК-управления  наблюдателем Калмана в условиях помех происходит как восстановление всех координат состояния системы, так и получение оптимальных характеристик системы.

При подаче помех на вход объекта происходит их фильтрация, в результате чего мы получаем «чистый» сигнал на выходе объекта, если помехи были поданы на измеряемый выход объекта, то приходиться прибегать к усложнению системы – использованию фильтра Калмана, чтобы отфильтровать их.

4.    Выводы

В ходе данной работы было проведено исследование оптимальной системы ЛК-управления с наблюдателем Калмана. Результаты всех испытаний приведены в соответствующих пунктах.

Из полученных результатов можно сделать следующие общие выводы:

–  получение оптимальных параметров системы при использовании ЛК-управления возможно только в случае измерения всех координат состояния объекта, либо использования модели для определения неизмеряемых параметров. Т.о. усложнение системы с неполностью наблюдаемым вектором состояния при использовании наблюдателя оправдано;

–  при нахождении системы в условиях помех типа «белый шум» фильтр Калмана позволяет восстановить все координаты состояния объекта, а ЛК-управление – оптимизировать переходную характеристику системы.