Исследование оптимальной системы ЛК – управления с наблюдателем Калмана. Трехмерная система представления модели RGB, страница 2

u – управление, формируемое  регулятором системы.

Коррекция прогнозируемого дискретной моделью объекта значений измеряемых координат состояния, производится в функции рассогласования(невязки - e(k+1) ) измеряемого и прогнозируемого значений,

e(k+1)=y(k+1)-(k+1)                                                    (3)

Невязка  умножается на коэффициент К коррекции предсказания.

В результате формируется вектор

  (4)

Для формирования новой оценки  (k+1) в алгоритме работы фильтра Калмана предварительно реализуется задача вычисления на каждом шаге корректирующего коэффициента .

Оптимальные значения корректирующего коэффициента на (k+1) шаге можно определить по формуле:

K(k+1)=Q(k+1)C^T[CQ(k+1)C^T+W]^-1      

где:

 - матрица дисперсии предсказания;

 - матрица дисперсии помехи измерения;

 – матрица (вектор – строка) измерений.

Вектор  используется для коррекции вектора оценки прогнозируемых координат состояния в виде:

                        (5)

Обратная связь (управление)  формируется как линейная функция оценочных значений полного вектора координат состояния, получаемого с выхода наблюдателя, т.е.

U(k)=u(k) = -K^* (k) ,                                                     (6)

где:

 - матрица (вектор-строка) оптимальных коэффициентов обратной связи, определяемых, например, методом динамического программирования.

Как было отмечено ранее, уравнение (6), задаваемое регулятором, является линейной функцией полного вектора оценочных значений (k), формируемых наблюдателем, а не объектом.

3.    Экспериментальная часть

3.1. Переход от скалярной формы записи исходного уравнения к векторно-матричной форме

Уравнение объекта задано линейным дифференциальным уравнением второго порядка:

где а₀, а₁, а₂, b – постоянные коэффициенты.

Исходные данные:  

 

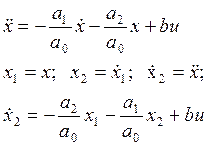
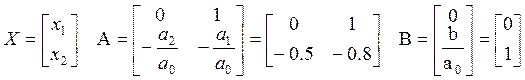
Схема набора для заданных исходных данных представлена на рис. 3.1.

Рис. 3.1. Схема набора для заданных исходных данных.

где                                          

3.2. Проверка адекватности наблюдателя и объекта

Схема лабораторной установки для исследования объекта представлена на рис. 3.2.1.

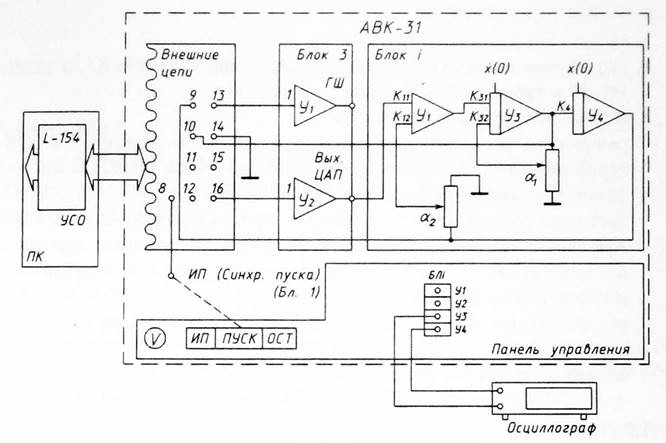
Рис. 3.2.1. Схема лабораторной установки.

Перед началом работы необходимо убедиться в адекватности объекта и модели без подключения ЛК-управления и определить параметры переходного процесса для них (время переходного процесса t_пп). Для этого необходимо подать на наблюдатель и объект одинаковое управляющее воздействие, одинаковые начальные условия и корректно задать матрицы

Возмущение U_С  = 0 В, x(0) = 2 В. Период дискретизации T₀ = 0,1 с.

В результате получены следующие значения:

 

Оптимальные коэффициенты:

Переходный процесс объекта и наблюдателя представлен на рис. 3.2.2.

Рис. 3.2.2. Переходный процесс объекта.

Из полученных результатов можно сделать вывод, что и наблюдатель, и объект являются адекватными.

Параметры переходного процесса для исследуемого объекта:

.

Погрешность восстановления выходной координаты . Относительная погрешность .

Погрешность восстановления ненаблюдаемой координаты (производной) . Относительная погрешность .

Таким образом, при полном совпадении параметров наблюдателя и объекта, наблюдатель полностью соответствует объекту.

В данном случае оптимальное ЛК-управление отключено, объект находится в разомкнутом состоянии.

3.3. Исследование системы ЛК – управления с полностью управляемыми координатами состояния объекта

В данном пункте рассматривается система без использования наблюдателя (модели объекта), т.к. все координаты состояния объекта измеряемы и в модели нет необходимости.

Оптимальные коэффициенты обратной связи:          

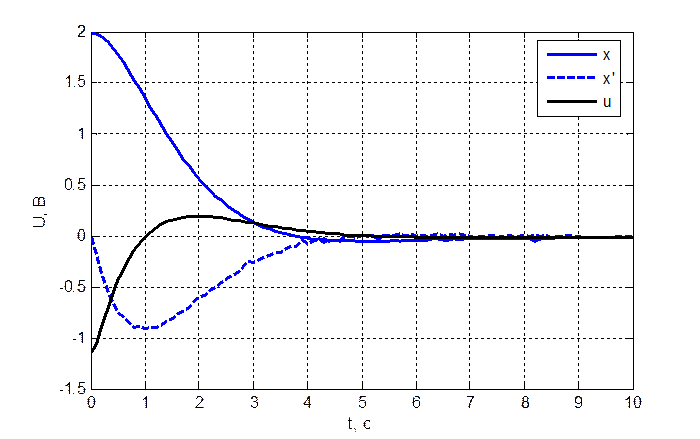
Рис. 3.3.1. Переходный процесс замкнутой системы при .

Критерии оптимальности:        

Время переходного процесса:         

Из полученных результатов можно сделать вывод, что при полностью наблюдаемом векторе состояния объекта происходит получение оптимальных характеристик переходного процесса.

3.4. Исследование системы ЛК – управления с не полностью управляемыми координатами состояния объекта

Оптимальные коэффициенты обратной связи:          

Рис. 3.4.1. Переходный процесс замкнутой системы при

Рис. 3.4.2. Переходный процесс объекта и наблюдателя при .