Санкт-Петербургский государственный политехнический университет
Факультет технической кибернетики
Кафедра автоматики и вычислительной техники
Дисциплина: компьютерные системы управления
Тема: Оценка неизмеряемых координат состояния объекта при случайных возмущениях (дискретный фильтр Калмана)
Выполнил студент гр. 5081/1
Проверил:
Санкт-Петербург
2009
1. Цель работы
Ознакомление с организацией и особенностью работы дискретного фильтра Калмана, предназначенного для оценки неизмеряемых координат состояния объекта, находящегося под воздействием помех типа белого шума как на входе, так и в канале измерения выходного сигнала.
2. Теоретические сведения
Характерной особенностью структуры данного фильтра является включение в его состав математической модели объекта, используемых для прогнозирования процессов прохождения сигнала через динамический объект. Такая структура позволяет заменить зашумлённый объект с не полностью измеряемыми координатами состояния адекватной ему моделью с полностью наблюдаемыми координатами. Кроме того, даже если какая-либо из координат измеряема, но зашумлена помехами – заменить её соответствующей координатой с модели объекта. При этом, если спектры полезного сигнала и помеха пересекаются, обеспечить минимизацию дисперсии помехи в выходном сигнале.
Таким образом, фильтром Калмана решаются две задачи – восстановление не измеряемых координат состояния объекта и фильтрация помех.
Алгоритм оценки состояния линейного объекта управления при случайных возмущениях (дискретный фильтр Калмана)
Пусть имеется линейный стационарный объект, координаты состояния которого в дискретные моменты времени описываются марковским процессом вида:
x(k+1)=Ax(k)+F(v(k)+u(k)) (1)
с измерителем выходных координат состояния, описываемым уравнением
y(k+1)=Cx(k+1)+w(k+1) (2)
В (1) и (2) использованы следующие обозначения:
x(k) – вектор состояния; xÎRn
v(k) – входной векторный случайный сигнал («белый шум») с ковариационной матрицей V; VÎRm
u(k) – входной детерминированный сигнал; uÎRm
y(k) – вектор выходных измерений; rÎRr
w(k) – вектор шума измерений с ковариационной матрицей W; wÎRr («белый шум»)
А – матрица системы,
А – матрица входа,
С – матрица измерений.
Требуется получить оценку вектора
состояния ![]() на основе измерений выхода y(k+1), содержащих случайные
погрешности в виде векторного белого шума w(k+1). Калмановская фильтрация использует идею прогнозирования
состояния объекта в (k+1)-й момент времени на основе
оценки координат состояния в k-й момент времени и
текущего измерения выходных координат y(k+1).
на основе измерений выхода y(k+1), содержащих случайные
погрешности в виде векторного белого шума w(k+1). Калмановская фильтрация использует идею прогнозирования
состояния объекта в (k+1)-й момент времени на основе
оценки координат состояния в k-й момент времени и
текущего измерения выходных координат y(k+1).
Прогнозируемые значения выходных координат сравнивается с измеренными и невязка (отличие прогнозируемого и измеренного значения) используется для коррекции оценки координат состояния в текущий (k+1)-й момент времени
При этом коррекция производится в форме аддитивного сигнала, получаемого путём умножения невязки на корректирующий коэффициент (коэффициент Калмана). Корректирующий коэффициент вычисляется на каждом шаге и обеспечивает реализацию требования получения оценки с минимальной дисперсией.
На рис. 2. приведена структурная схема объекта, заданного в форме (1) и (2), и фильтра Калмана, реализующего описанную выше идею коррекции прогнозированного значения координат состояния объекта для (k+1)-го момента времени.
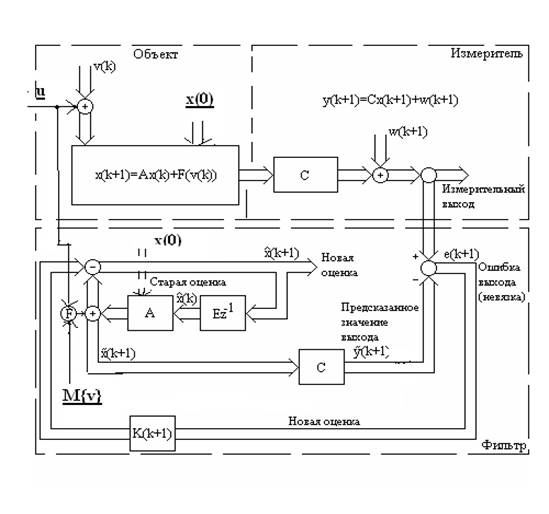
Рис. 2.1. Структурная схема дискретного фильтра Калмана.
Очевидно, что основной проблемой при этом будет вычисление корректирующего коэффициента К(к+1). Здесь предлагается использование метода фильтрации с минимальной дисперсией.
При использовании метода фильтрации с минимальной дисперсией формируется взвешенное среднее х двух независимых векторных оценок х1 и х2 в виде
![]() =x1+K*(x2-x1) (3), где К* – весовая матрица
размерностью n´n, причём К* = КС.
=x1+K*(x2-x1) (3), где К* – весовая матрица
размерностью n´n, причём К* = КС.
Матрица К выбирается так, чтобы
дисперсия ![]() была минимальной.
была минимальной.
Если принять, что Сх2=у2,
то оценку ![]() (3) можно переписать следующим
образом:
(3) можно переписать следующим
образом:
![]() =х1+К(у2-Сх1)
(4), здесь К – корректирующая
матрица.
=х1+К(у2-Сх1)
(4), здесь К – корректирующая
матрица.
Применительно к рассматриваемому объекту (1) и (2)примем:
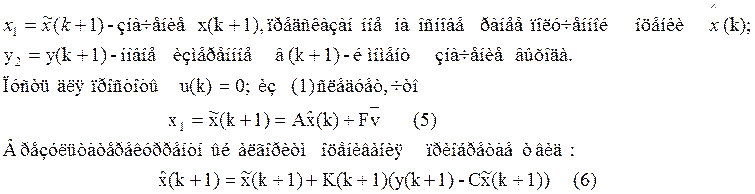
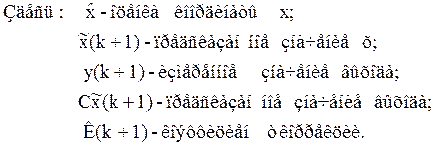
Значение коэффициентов коррекции можно получить в виде:
K(k+1)=Q(k+1)CT[CQ(k+1)CT+W]-1 (7)
где Q(k+1) – ковариационная матрица оценки предсказанного
значения ![]()
![]() (k+1).
(k+1).
Для объекта (1) с учётом u(k)=0 получим
Q(k+1)=AP(k)AT+FVFT (8)
где P(k) – ковариационная матрица оценки ![]() на
k-ом шаге, причём,
на
k-ом шаге, причём,
P(k)=Q(k)-K(k)CQ(k) (9)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.