Оценка неизмеряемых координат состояния объекта при случайных возмущениях (дискретный фильтр Калмана), страница 3

3.4. Исследование работы наблюдателя при различных значениях управления объекта и модели

В данном пункте  , .

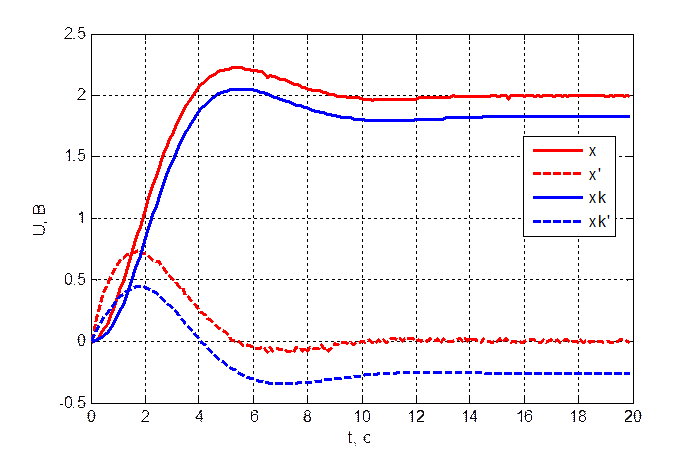
Рис. 3.4.1. Переходный процесс объекта и модели при .

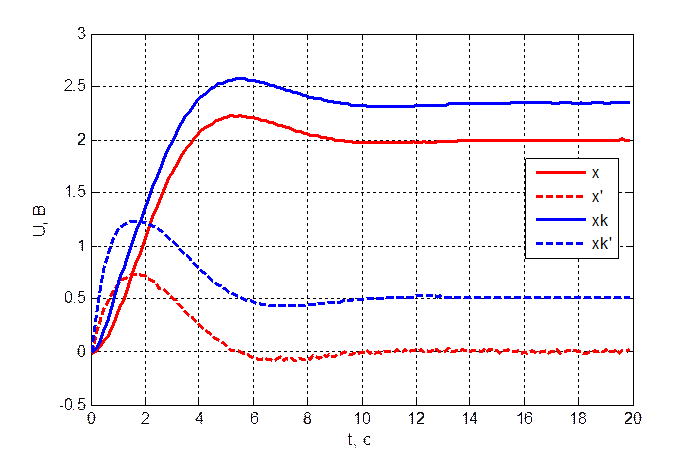
Рис. 3.4.2. Переходный процесс объекта и модели при .

При различных значениях управления, подаваемого на объект и модель, наблюдатель восстанавливает измеряемую и неизмеряемую координату с некоторой статической ошибкой. Так для измеряемой выходной координаты она равна 0,3 В, а для скорости 0,5В. С чем связана такая ошибка установить не удалось.

3.5. Исследование работы наблюдателя при изменении периода дискретизации

В данном пункте .

Переходный процесс объекта и модели при  представлен на рис. 3.5.1.

В результате получены следующие значения:

Переходный процесс объекта и модели при  представлен на рис. 3.5.2.

В результате получены следующие значения:

 

Переходный процесс объекта и модели при  представлен на рис. 3.5.3.

В результате получены следующие значения:

Рис. 3.5.1. Переходный процесс объекта и модели при .

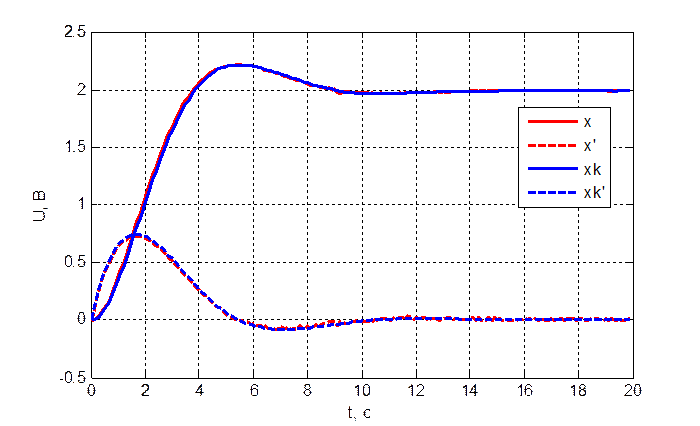
Рис. 3.5.2. Переходный процесс объекта и модели при .

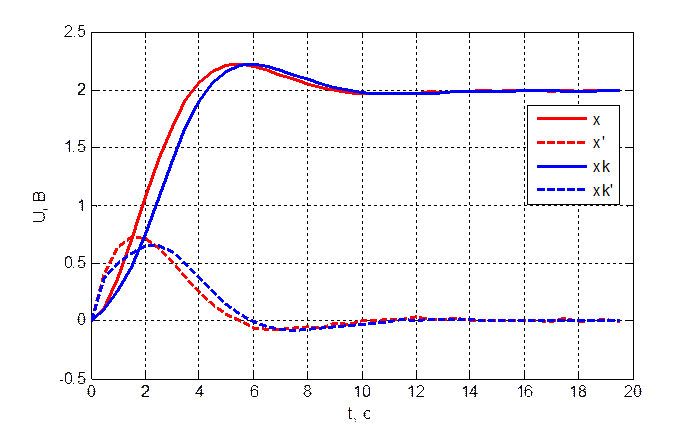
Рис. 3.5.3. Переходный процесс объекта и модели при .

Из полученных результатов можно сделать вывод, что при увеличении периода дискретизации, время, затрачиваемое на восстановление координат состояния объекта, увеличивается. Следовательно, качество восстановления ухудшается. Т.о. необходимо выбирать период дискретизации минимум на два порядка меньше времени переходного процесса в объекте.

Таблица 3.5.1. Результаты абсолютной и относительной погрешности

восстановления координат состояния объекта.

Параметры объекта и модели
	0,0163	0,73	0,0015	0,21
	0,0073	0,32	0,0016	0,22
	0,0413	1,86	0,0029	0,39

Относительные погрешности восстановления координат состояния объекта при заданных значениях периода дискретизации не выходят за допустимый предел (10%). Т.о. применение наблюдателя при заданных параметрах вполне оправдано.

3.6. Исследование работы наблюдателя в условиях шума

В данной части работы производилось изучение сигнала, находящегося под воздействием помех типа белого шума как на входе, так и в канале измерения выходного сигнала. Задачей наблюдателя было восстановить полученный сигнал.

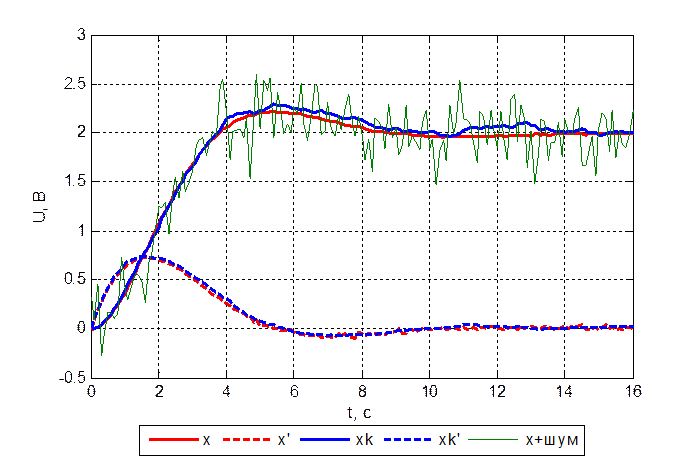
Рис. 3.6.1. Переходный процесс объекта и модели при .

Из полученных результатов можно сделать вывод, что работа фильтра Калмана в условиях помех весьма эффективна.

Данный фильтр позволяет восстановить с допустимой погрешностью в условиях помех как измеряемые координаты состояния объекта, так и неизмеряемые.

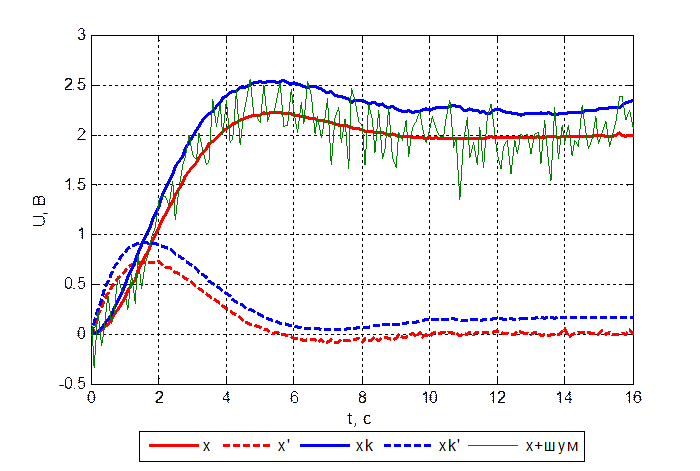
Рис. 3.6.2. Переходный процесс объекта и модели при .

Из полученных результатов можно сделать вывод, что наблюдатель восстанавливает измеряемую и неизмеряемую координату с некоторой статической ошибкой. Так для измеряемой выходной координаты она равна 0,25 В, а для скорости 0,2 В.

Рис. 3.6.3. Переходный процесс объекта и модели при .

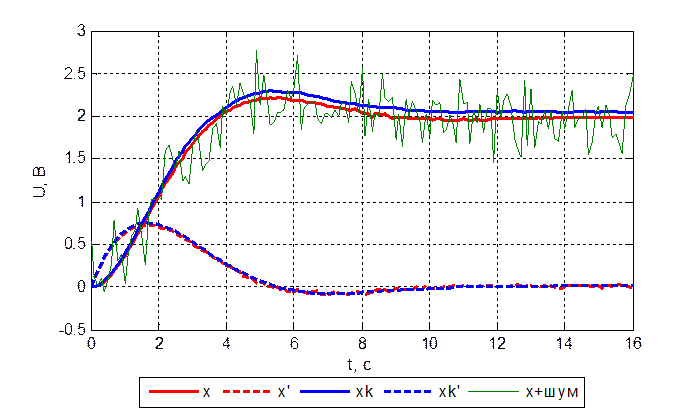
Рис. 3.6.4. Переходный процесс объекта и модели при .

Из полученных результатов можно сделать вывод, что наблюдатель при большой дисперсии помехи ввода не достаточно точно восстанавливает измеряемую и неизмеряемую координату. При большой дисперсии помехи измерения наблюдатель восстанавляет измеряемую координату со статичтической ошибкой = 0,1 В, а  неизмеряемую – точно.

4.    Выводы

В ходе данной работы было проведено исследование дискретного фильтра Калмана. Результаты по каждой части работы приведены в соответствующих пунктах. Из полученных результатов можно сделать следующие  общие выводы:

–  при полном совпадении параметров модели и объекта фильтр полностью подстраивается под объект и восстанавливает как измеряемые, так и неизмеряемые координаты;

–  при несовпадении начальных условий объекта и модели фильтр Калмана восстанавливает координаты состояния объекта с допустимой погрешностью, следовательно, может быть применим;

–  при несовпадении управления объекта и модели фильтр восстанавливает координаты состояния объекта с некоторой статической ошибкой, следовательно, его применение при данных условиях затруднено;

–  состояния объекта, увеличивается. Т.о. необходимо выбирать период дискретизации минимум на порядок меньше времени переходного процесса в объекте;

–  работа фильтра Калмана в условиях помех весьма эфективна. Данный фильтр позволяет восстановить с допустимой погрешностью как измеряемые координаты состояния объекта, так и неизмеряемые;

–  при некорректном задании параметров помех фильтр восстанавливает координаты состояния объекта с некоторой статической ошибкой, следовательно, его применение при данных условиях затруднено.