Оценка неизмеряемых координат состояния объекта при случайных возмущениях (дискретный фильтр Калмана), страница 2

Если |u | > 0   и его можно измерить, то вычисление x(k+1) требуется производить, используя модификацию выражения (5), следующим образом:

(k+1) = A(k) + F(+u(k))      (10)

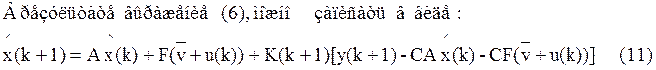
Уравнения  (6) и (11) является формальным отражением  основной идеи дискретного  наблюдателя Калмана -  прогнозирование  координат состояния  для  (k+1)  шага по данным  оценок, полученным на k-м  шаге с  возможной  коррекцией  прогноза.

Алгоритм реализации дискретного фильтра Калмана для линейного стационарного объекта

Исходные данные:

A –матрица параметров дискретного объекта,

F -  матрица параметров входа дискретного объекта,

C – матрица измерений

V, W –МО и дисперсии случайных сигналов соответственно на входе и в цепи измерения выходного сигнала объекта,

k = 0 –начальное содержание счетчика циклов,

N_max – максимальное число циклов

P(0) =[0]  - начальное значение ковариационной  матрицы  оценки 

U(x) – входной сигнал

Шаг 1. Ввод исходных данных

Шаг 2. k=k+1

Шаг 3. Формирование предсказываемого значения вектора состояний:

Шаг 4. Получение невязки измерения:

Шаг 5. Вычисление ковариационной матрицы оценки предсказаний

Q(k+1)=AP(k)A^T+FVF^T

Шаг 6. Определение коэффициента коррекции:

K(k+1)=Q(k+1)C^T[CQ(k+1)C^T+W]^-1=Q(k+1) C^т/ (CQ(k+1)C^т +W)

Шаг 7. Формирование корректирующего сигнала:

Шаг 8. Формирование оценки вектора состояний

Шаг 9. Вычисление ковариационной матрицы оценки:

P(k+1)=Q(k+1)-K(k+1)CQ(k+1)=(E- K(k+1)C)Q(k+1)

Шаг 10. Если k<N _max, то  P(k)=P(k+1),  и  переход к шагу 2, иначе - к шагу 11

Шаг 11. Вывод результата

Шаг 12. Конец.

3.    Экспериментальная часть

3.1. Переход от скалярной формы записи исходного уравнения к векторно-матричной форме

Уравнение объекта задано линейным дифференциальным уравнением второго порядка:

где а₀, а₁, а₂, b – постоянные коэффициенты.

Исходные данные:  

 

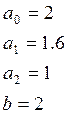
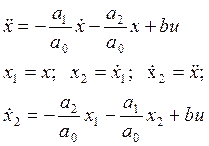
Схема набора для заданных исходных данных представлена на рис. 3.1.

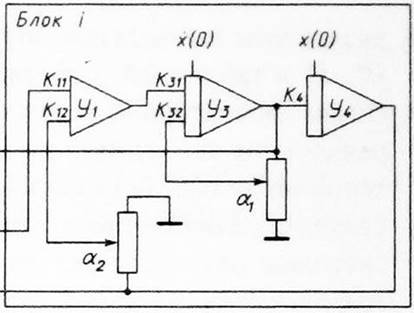
Рис. 3.1. Схема набора для заданных исходных данных.

где                                          

3.2. Проверка адекватности модели и объекта

Схема лабораторной установки для исследования объекта представлена на рис. 3.2.1.

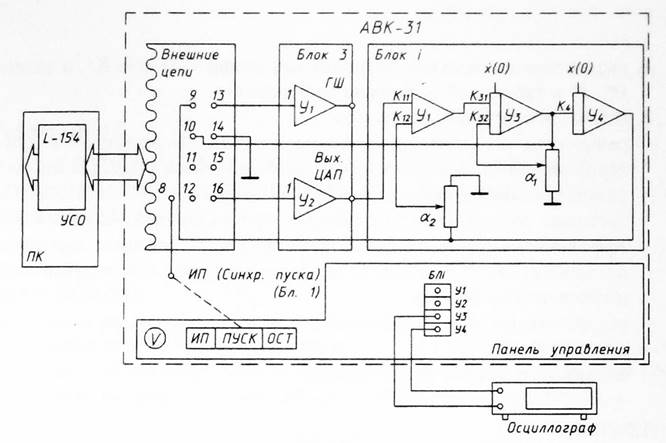
Рис. 3.2.1. Схема лабораторной установки.

Перед началом работы необходимо убедиться в адекватности объекта и модели и определить параметры переходного процесса для них (время переходного процесса t_пп). Для этого необходимо подать на модель и объект одинаковое управляющее воздействие, одинаковые начальные условия и корректно задать матрицы

Возмущение U_С  = 1 В, x(0) = 0 В. Период дискретизации T₀ = 0,1 с.

В результате получены следующие значения:

 

Случайный сигнал (белый шум) = 0.

Переходный процесс объекта и модели представлен на рис. 3.2.2.

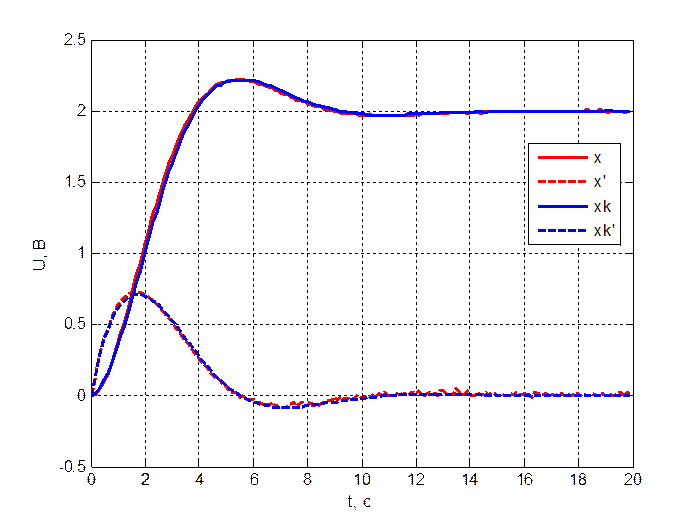
Рис. 3.2.2. Переходный процесс объекта.

Из полученных результатов можно сделать вывод, что и модель, и объект являются адекватными.

Параметры переходного процесса для исследуемого объекта:

.

Погрешность восстановления выходной координаты . Относительная погрешность .

Погрешность восстановления ненаблюдаемой координаты (производной) . Относительная погрешность .

Таким образом, при полном совпадении параметров модели и объекта наблюдатель полностью подстраивается под объект.

3.3. Исследование работы наблюдателя при несовпадении начальных условий объекта и модели

Управление по возмущению

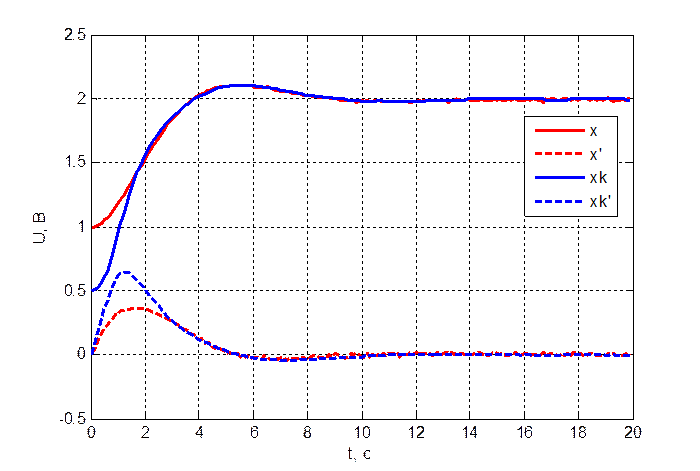
Рис. 3.3.1. Переходный процесс объекта и модели при .

Рис. 3.3.2. Переходный процесс объекта и модели при .

Рис. 3.3.3. Переходный процесс объекта и модели при .

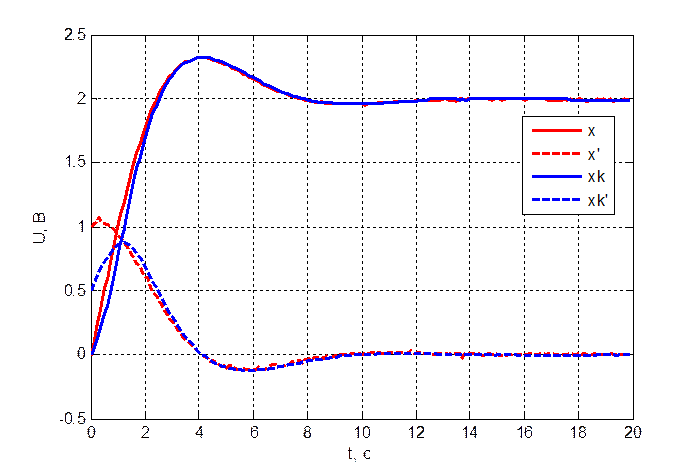
Рис. 3.3.4. Переходный процесс объекта и модели при .

Из полученных результатов можно сделать вывод, что при несовпадении начальных условий по координате и по скорости модели и объекта, восстановление как измеряемой, так и неизмеряемой координаты происходит только через 3-4 секунды, что соответствует трети времени переходного процесса. Т.е. восстановление происходит достаточно плохо.

Таблица 3.3.1. Результаты абсолютной и относительной погрешности восстановления координат состояния объекта при различных начальных условиях.

Параметры объекта и модели
	0,0224	2,24	0,0168	4,6
	0,0242	0,96	0,0329	17,3
	0,0141	2,82	0,0115	1,49
	0,0161	1,41	0,0164	1,53

Из полученных результатов можно сделать вывод, что при несовпадении наблюдаемых координат восстановление происходит значительно хуже, чем при несовпадении ненаблюдаемых. Заметим, что относительная погрешность восстановления по скорости превышает допустимые пределы (10%).