4.14. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() ; 10)
; 10) ![]() ; 11)
; 11) ![]() ; 12)
; 12) 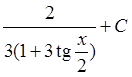 ; 13)
; 13) 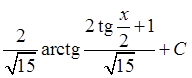 ; 14)
; 14) ![]() ; 15)
; 15) ![]() ; 16)
; 16) ![]() ; 17)
; 17) ![]() ; 18)
; 18) 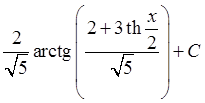 ; 19)
; 19) ![]() ; 20)
; 20) ![]() ; 21)
; 21) ![]() ; 22)
; 22) 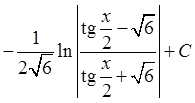 ; 23)
; 23) ![]() ; 24)
; 24) 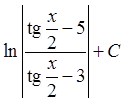 ; 25)
; 25) 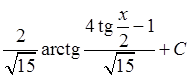 ; 26)
; 26) ![]() ; 27)
; 27) ![]() ; 28)
; 28) ![]() ; 29)
; 29) ![]() ;30)
;30) ![]() ; 31)
; 31) ![]() ; 32)
; 32) ![]() ; 33)
; 33) ![]() .
.
4.15. 1) ![]() ; 2)
; 2) ![]() ;
;
3) ![]() ;
4)
;
4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]()
![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() .
.
4.16. 1)![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) 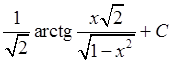 ; 8)
; 8) 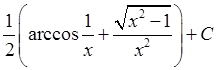 ; 9)
; 9) ![]() ; 10)
; 10) ![]() ; 11)
; 11) ![]() ; 12)
; 12) 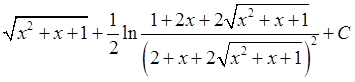 ; 13)
; 13) ![]() ; 14)
; 14) 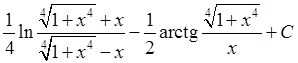 ; 15)
; 15) ![]() ;16)
;16) 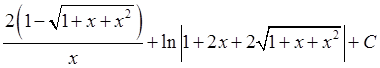 ; 17)
; 17) ![]() ; 18)
; 18) ![]() ; 19)
; 19) ![]() ; 20)
; 20) ![]() ; 21)
; 21) ![]() ; 22)
; 22) 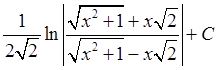 ; 23)
; 23) ![]() ; 24)
; 24) ![]() ; 25)
; 25) ![]() ; 26)
; 26) ![]() ; 27)
; 27) 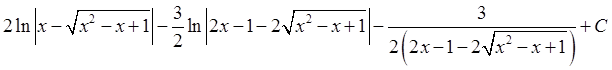 ; 28)
; 28) ![]() ; 29)
; 29) ![]() ; 30)
; 30) ![]() ; 31)
; 31) 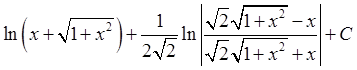 ; 32)
; 32) 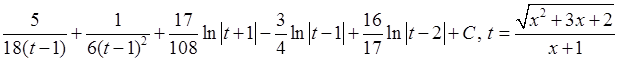 ; 33)
; 33) ![]() ; 34)
; 34) ![]() .
.
4.17. 1) ![]() ; 2) ; 3)
; 2) ; 3) ![]() ; 4)
; 4) 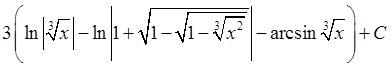 ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() ; 10)
; 10) ![]() ; 11)
; 11) 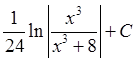 ; 12)
; 12) ![]() ; 13)
; 13) ![]() ; 14)
; 14) ![]() ; 15)
; 15) ![]() ; 16)
; 16) ![]() ; 17)
; 17) ![]() ;18)
;18) ![]() ; 19)
; 19) ![]() ; 20)
; 20) 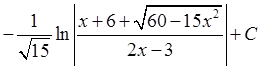 ; 21)
; 21) ![]() ; 22)
; 22) ![]() ; 23)
; 23) ![]() ; 24)
; 24) ![]() ; 25)
; 25) ![]() ; 26)
; 26) ![]() ; 27)
; 27) ![]() ; 28)
; 28) ![]() ; 29)
; 29) ![]() ; 30)
; 30) ![]() ; 31)
; 31) ![]() ; 32)
; 32) ![]() ;
;
33) ![]() ;
34)
;
34) ![]() ; 35)
; 35) ![]() ; 36)
; 36) ![]() ;
;
37) ![]() ;
38)
;
38) ![]() ;
;
39) ![]() ;
;
40) ![]() ;
41)
;
41) ![]() ; 42)
; 42) ![]() ; 43)
; 43) ![]() ; 44)
; 44) ![]()
![]()
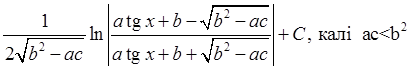 .
.
ЗМЕСТ
1. Уводзіны ў матэматычны аналіз . . . . . . . . . . . . . . . 3
1.1. Мноствы. Выказванні. Метад матэматычнай індукцыі . . . . 3
1.2. Рэчаісныя і камплексныя лікі . . . . . . . . . . . . . . 10
1.3. Камбінаторыка і біном Ньютана . . . . . . . . . . . . . 17
1.4. Мнагасклады . . . . . . . . . . . . . . . . . . . . . 21
2. Ліміты і непарыўнасць . . . . . . . . . . . . . . . . . . . 28
2.1. Лікавыя функцыі і паслядоўнасці . . . . . . . . . . . . . 28
2.2. Ліміт паслядоўнасці . . . . . . . . . . . . . . . . . . 33
2.3. Ліміт функцыі . . . . . . . . . . . . . . . . . . . . 44
2.4. Непарыўнасць функцыі . . . . . . . . . . . . . . . . 49
2.5. Параўнанне функцый . . . . . . . . . . . . . . . . . 55
3. Дыферэнцыяльнае злічэнне функцый адной зменнай . . . . . . 63
3.1. Вытворная. Формуля і правілы вылічэння вытворных . . . . 63
3.2. Геаметрычны і фізічны сэнс вытворных . . . . . . . . . . 70
3.3. Дыферэнцыял функцыі . . . . . . . . . . . . . . . . . 75
3.4. Вытворныя і дыферэнцыялы вышэйшых парадкаў . . . . . 79
3.5. Правіла Лёпіталя . . . . . . . . . . . . . . . . . . . 83
3.6. Формула Тэйлара . . . . . . . . . . . . . . . . . . . 85
3.7. Даследаванне функцыі і будаванне графіка . . . . . . . . 91
3.8. Знаходжанне найбольшых і найменшых значэнняў . . . . . 97
4. Нявызначаны інтэграл . . . . . . . . . . . . . . . . . . . 101
4.1. Агульныя спосабы інтэгравання . . . . . . . . . . . . . 101
4.2. Асноўныя метады інтэгравання . . . . . . . . . . . . . 103
4.3. Інтэграванне рацыянальных функцый . . . . . . . . . . 106
4.4. Інтэграванне трыганаметрычных і гіпербалічных функцый . . 110
4.5. Інтэграванне ірацыянальных функцый . . . . . . . . . . 115
4.6. Інтэграванне розных функцый . . . . . . . . . . . . . . 120
Адказы і парады . . . . . . . . . . . . . . . . . . . . . . 122
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.