Адказы і парады. Акружына радыуса 1 з цэнтрам у пункце. Пункты разрыву першага тыпу, страница 7

(0, +∞), выпуклая ўніз на (–∞, 0); 10) –2; выпуклая ўверх на (–∞, –2), выпуклая ўніз на (–2, +∞); 11) 1/2;  выпуклая ўверх на (1/2, +∞), выпуклая ўніз на  (–∞,   l/2); 12) ; выпуклая ўверх на (0, ), выпуклая ўніз на (, +∞).  3.129. 1) (,

); 2) (–, ); 3) (9/2, 27/2). 3.131. 1) y=2x; 2) x = –- 2/3,  y = 5/3; 3) x = ±2; 4) x = 2; 5) y = x + 2; 6) y = x + π/2 пры x → +∞, y = x – π/2 пры x → –∞. 

3.132. 1) Пункты перасячэння з восямі каардынат (–2, 0), (1,  0),  (0,  2); y_max = 4 пры x = –1,  y_min = 0 пры x = l;  пункт перагіну x = 0; 2) Пункты перасячэння з восямі каар-дынат  (0, 0) (1, 0);  y_max = 1 пры х = 1, y_min = 0 пры x = 2; пункты перагібу x = l/2, х = 4;

3) Пункты перасячэння з восямі каардынат (0, 0), (0, 2); y_max = 1 пры x = = 1, y_min = 0 пры x = 0, y_min = 0 пры x = 2; пункт перагібу х = 3 ± .

3.133. 2) P₂(x) = (3x²–1); пункты перасячэння з восямі  каардынат (±1/, 0), 

(0, –1/2); цотная; y_min = –l/2 пры x = 0; 3) P₃(x) = (5x³ – 3x); пункты перасячэння з восямі каардынат (0, 0), (0, ±); няцотная; y_max = –1/ пры x = –l/,

y_min = –1/ пры x = 1/; пункт перагібу х = 0; 4) P₄(x )= (35x⁴ – 30x² + 3); пункты перасячэння з восямі каардынат (±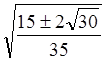, 0), (0, –3/8);  цотная; y_min = 3/7 пры x = ±, y_max = 3/8 пры x = 0. 3.134. 1) Абсяг вызначэння:  x ≠ ±1; пункт пера-сячэння з восямі каардынат (0, 0); асімптота x = l; y_max = 27/4 пры x = 3/2; пункт пера-гіну x = 0; 2) Абсяг  вызначэння: x ≠ –1, x≠ 3; пункт перасячэння з восcю ардынат

(0, 1); асiмптоты x = –l, x = 3, y = 1; y_max = –2 +  пры x = (1 – )/2; y_min = –2 – пры x = (1 + )/2; пункт перагіну x ≈ 1,7; 3) Абсяг вызначэння: x ≠ 0, x≠ 1; пункты перасячэння з восямі каардынат (1, 0),  (0, –1); асімптоты x = –1, x = 4, y = 0; пункт перагіну x ≈ l,33.  4) Абсяг вызначэння: x ≈ 0, x ≠ 1; пункт перасячэння з воссю каар-дынат (1/2, 0); асімптоты x = 0, x = 1; пункт перагіну x = l/2; 5) Абсяг вызначэння:

x ≠ 2; пункт перасячэння з восямі каардынат (1, 0), (0, –1/4); асiмптот x = 2; y_min = 27/4 пры x = 4; пункт перагіну x = l; 6) Абсяг вызначэння: x ≠ 0; асімптоты x = 0, y = x;

y_max = 5 пры x = 1, y_max = –17/3 пры x = –3, y_min = 19/4 пры x = 2; пункт перагіну x = 9/7; 7) Абсяг вызначэння: x ≠ –1; пункт перасячэння з восямі каардынат (0, 0); асiмптоты x = –1, y = x – 3; y_max = 256/97 пры x = –4, y_min = 0 пры x = 0; 8) Пункты перасячэння з восямі каардынат (1, 0), (0, 10/9); асімптота y = 0; y_max ≈ –1,2 пры x = –1,5, y_max ≈ 0,88 пры x = = 3, y_min = 0 пры x = 1; 2) Абсяг вызначэння: (–∞,–1), (1, +∞); асімптота, y = 0;

10) Пункт перасячэння з восямі каардынат (0, 0); y_min = 0 пры x = 0; 11) Пункт пера-сячэння з восямі каардынат (0, 5), (0, 0); y_max = 3 пры x = 3; y_min = 5 пры x = 0; 12) Абсяг вызначэння: х ≠ –2; пункт перасячэння з восямі каардынат (0, 0); асiмптоты x = –2, y = 0; y_max =  пры x = 4; y_min = 0 пры x = 0; пункты перагіну x ≈ –0,2, x ≈ –8,2; 13) асімптоты y = x пры х→ −∞; y_min = –1 пры x = 0; 14) Пункт перасячэння з воссю ардынат (0, e^–1); асімптота y = 0; y_max = 1 пры x = 1; пункты перагіну x = 1 ± 1/; 15) Пункты перасячэння з восямі каардынат (–1, 0), (0, l/e); асімптота y = 0 пры

x → +∞; y_min = 0 пры x = –1; y_max = 4e^–1 пры x = –1; пункты перагіну х = (1 ± )/2; 16) Абсяг вызначэння: x > 0; пункт перасячэння з воссю (1, 0); ;

у_min =–1/(2) пры х = 1/; пункт перагіну x = l/; 17) Перыядычная з перыядам π; цотная; на перыядзе [0,π]: пункты перасячэння з восямі каардынат (0, 0), (π/3, 0), (2π/3, 0); y_min = 0 пры x = 0, у_min = –1 пры x = π/2; y_max = 9/16 пры x = arccos ≈ 1,3 і пры x = π – arccos ≈ 1,8; пункты перагіну x = arccos ≈ 0,34,

x = π –arccos ≈ 2,8, x = (π – arccos) ≈ 1,1,