2.136.1) ![]() –
пункты разрыву першага тыпу; 2)
–
пункты разрыву першага тыпу; 2) ![]() –
пункт ска-савальнага разрыву; 3)
–
пункт ска-савальнага разрыву; 3) ![]() –
пункт разрыву другога ты-пу; 4)
–
пункт разрыву другога ты-пу; 4) ![]() ,
, ![]() – пунк-ты разрыву другога
тыпу; 5)
– пунк-ты разрыву другога
тыпу; 5) ![]() – пункт скасавальнага
разрыву; 6)
– пункт скасавальнага
разрыву; 6) ![]() – пункты разрыву
другога тыпу;7)
– пункты разрыву
другога тыпу;7) ![]() – пункты разрыву
другога тыпу,
– пункты разрыву
другога тыпу, ![]() – пункт скасавальнага
разрыву; 8)
– пункт скасавальнага
разрыву; 8) ![]() – пункт разрыву першага тыпу; 9)
– пункт разрыву першага тыпу; 9) ![]() – пункт разрыву другога тыпу,
– пункт разрыву другога тыпу, ![]() – пункт скасавальнага разрыву. 2.138. 1)
– пункт скасавальнага разрыву. 2.138. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() ; 7)
; 7) ![]() . 2.139.
. 2.139. ![]() .
.
2.140. ![]() . 2.142.
. 2.142. ![]() .
2.145. Не.
.
2.145. Не.
2.147. 1) ![]() , калі
, калі ![]() ;
;
![]() , калі
, калі ![]() ;
;
![]() , калі
, калі ![]() ;
;
![]() ,
, ![]() –
пункты разрыву першага тыпу; 2)
–
пункты разрыву першага тыпу; 2) ![]() , калі
, калі ![]() ;
; ![]() ,
калі
,
калі ![]() ;
; ![]() –
пункты скасавальнага разрыву; 3)
–
пункты скасавальнага разрыву; 3) ![]() ,
калі
,
калі ![]() ;
; ![]() ,
калі
,
калі ![]() ; функцыя непарыўная;
4) функцыя разрыўная пры ўсіх
; функцыя непарыўная;
4) функцыя разрыўная пры ўсіх ![]() .
.
2.151. 1)![]() дасягаецца;
дасягаецца; ![]() не дасягаецца; 2)
не дасягаецца; 2) ![]() дасягаецца;
дасягаецца; ![]() дасягаецца; 3)
дасягаецца; 3) ![]() не дасягаецца;
не дасягаецца; ![]() дасягаецца. 2.161. 1) а) раўнамерна
непарыўная на
дасягаецца. 2.161. 1) а) раўнамерна
непарыўная на ![]() , б) не з’яўляецца
раўнамерна непарыўнай на
, б) не з’яўляецца
раўнамерна непарыўнай на ![]() ; 2), 3),
4а) – раўнамерна непарыўная на
; 2), 3),
4а) – раўнамерна непарыўная на ![]() ; 4б) не
з’яўляецца раўнамерна непарыўнай на
; 4б) не
з’яўляецца раўнамерна непарыўнай на ![]() . 2.162. Парада:
дакажыце выкананне ўмовы крытэра Кашы існавання ліміта функцыі. 2.163. Парада:
скарыстайце задачу 2.162.
. 2.162. Парада:
дакажыце выкананне ўмовы крытэра Кашы існавання ліміта функцыі. 2.163. Парада:
скарыстайце задачу 2.162.
2.164. Парада: скарыстайце задачу 2.163. 2.165. 1), 2), 3), 4) – так.
2.166. 1а), 1б), 2а), 3б). 2.169. 1) 1; 2) 1; 3) 2; 4) 1/2; 5) ![]() ; 6) 2; 7) 2;
; 6) 2; 7) 2;
2.170. 1) 2; 2) 1; 3) 2; 4) 1; 5) 6; 6) ![]() .
2.172. 1); 3); 5); 9); 2.173. 1) Не; 2) так; 3) не;
.
2.172. 1); 3); 5); 9); 2.173. 1) Не; 2) так; 3) не;
4) не. 2.179. 1) – 7). 2.180. 1)
і 2); 3) і 6); 4) і 8); 5) і 7). 2.184. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]()
![]() .
2.189. 1)
.
2.189. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() +
+![]()
![]() ; 4)
; 4) ![]() ; 5)
; 5)![]() ;
6)
;
6) ![]()
![]()
![]() ;
;
7) ![]() ,
парада:
,
парада: 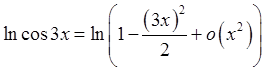 ; 8)
; 8) ![]() . 2.190. 1)
. 2.190. 1) ![]() , парада: скарыстаць роўнасць
, парада: скарыстаць роўнасць 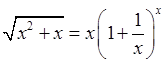 ; 2)
; 2)![]() ;
3)
;
3)![]() ; 4)
; 4)![]() .
.
2.191. 1) 5/2; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5) 1; 6)
; 5) 1; 6) ![]() ; 7) Парада: разглядзець выпадкі:
; 7) Парада: разглядзець выпадкі: ![]() ,
, ![]() ,
, ![]() ;
8) 1; 9)
;
8) 1; 9) ![]() . 2.192. 1) –1; 2)
. 2.192. 1) –1; 2) ![]() ; 3)
; 3) ![]() ; 4 )
; 4 )![]() . 2.193. Любы лік
. 2.193. Любы лік ![]() , такі, што
, такі, што ![]() . 2.194. 1) 1; 2) –1;
3) 0; 4)
. 2.194. 1) 1; 2) –1;
3) 0; 4) ![]() .
.
3.1. 1) 2x; 2) x–2/3/3; 3) 3cos3х; 4) 3xln3. 3.2. 1) (6 – ![]() )/(6
)/(6![]() (2 +
(2 + ![]() )2),
x >
0;
2) 2xctgx – (x2 +1)/sin2x, x ≠ πn,
)2),
x >
0;
2) 2xctgx – (x2 +1)/sin2x, x ≠ πn, ![]() ;
3) –ln2/(xln2x), x > 0, x ≠ 1;
;
3) –ln2/(xln2x), x > 0, x ≠ 1;
4) arcsinx+х/![]() , ׀x׀<1; 5) 2x(ln2·lnx + 1/x), x > 0; 6) chx(ch2x + 2sh2x);
, ׀x׀<1; 5) 2x(ln2·lnx + 1/x), x > 0; 6) chx(ch2x + 2sh2x);
7) (sh2x + 2xlnx)/2xch2x, x > 0; 8) (sin(1/x))/x2, x ≠ 0;
9) –2(x/sin2x2 + (sin22x)/cos42x), x ≠![]() ,
, ![]() ; 10) 1/
; 10) 1/![]() , 1–
, 1–![]() <x<1+
<x<1+![]() ;
11) 1/(1+x2), x≠1;
;
11) 1/(1+x2), x≠1;
12) –3tg2xsec2xsin(2tg3x)cos(cos2(tg3x)); 13) –cos2x, x ≠ π/2 + πk, x ≠ –π/4 + πn, k,n![]() ;
;
14) ![]() (1
+
(1
+ ![]() (1 +
(1 + ![]() ));
15) y(ln(a/b) + (b-a)/x), x > 0; 16) 1/
));
15) y(ln(a/b) + (b-a)/x), x > 0; 16) 1/![]() ;
;
17) 6/(xlnxln(ln3x)), x > e;
18) 4x/(x4 – 1), |x| > 1; 19) (6lge·lg2x2)/x, x≠0; 20) ln(x+![]() );
21) 1/sinx, 2kπ <x <π + 2kπ, k
);
21) 1/sinx, 2kπ <x <π + 2kπ, k![]() ;
22) 2sin(lnx), x > 0; 23) sgn(cosx), x ≠ π/2 + kπ, k
;
22) 2sin(lnx), x > 0; 23) sgn(cosx), x ≠ π/2 + kπ, k![]() ;
;
24) (xarcsinx)/(1 – x2)3/2, |x| < 1; 25) 2![]() , |x| < a;
, |x| < a;
26) 1 + xx(1 +
lnx) +![]() (1 + xlnx(1 + lnx)), x > 0; 27)
(1 + xlnx(1 + lnx)), x > 0; 27) ![]() (1 + alnx) + ax
(1 + alnx) + ax![]() (lnalnx + 1/x) + xx
(lnalnx + 1/x) + xx![]() lna(1 + lnx), x > 0;
lna(1 + lnx), x > 0;
28) ![]() , x > 0; 29) (sinx)cosx+1(ctg2x – lnsinx) – (cosx)sinx + 1(tg2x – lncosx), 2kπ <x <π/2 + 2kπ, k
, x > 0; 29) (sinx)cosx+1(ctg2x – lnsinx) – (cosx)sinx + 1(tg2x – lncosx), 2kπ <x <π/2 + 2kπ, k![]() ; 30) th3x; 31) –2/sh3x, x > 0; 32) 1/ch2x; 33)(sgn(shx)) /chx, x ≠ 0.
; 30) th3x; 31) –2/sh3x, x > 0; 32) 1/ch2x; 33)(sgn(shx)) /chx, x ≠ 0.
3.3. 1) sgnx,
x ≠ 0, y'(0) не існуе;
2) 2|x|. 3.4. φ(a). 3.5. 1) ![]() ; 2) 2;
3) ln4;
4) –(2/π)π/2(1 + ln(π/2)).
3.6. 1)
; 2) 2;
3) ln4;
4) –(2/π)π/2(1 + ln(π/2)).
3.6. 1) ![]() (2) = –1,
(2) = –1, ![]() (2) = 1; 2)
(2) = 1; 2) ![]() (1) = –2ln2,
(1) = –2ln2, ![]() (1) = 2ln2;
(1) = 2ln2;
3) ![]() (0) = –1,
(0) = –1, ![]() (0) = 1; 4)
(0) = 1; 4) ![]() (–1) = +∞,
(–1) = +∞, ![]() (–1) не існуе; 5)
(–1) не існуе; 5) ![]() (0) = 2,
(0) = 2, ![]() (0) = 0; 6)
(0) = 0; 6) ![]() (0) = 1,
(0) = 1, ![]() (0) = 0. 3.7 1)
а)так; б)так; 2) а)так; б)не; 3) а)так; б)не; 4) а)так; б)так.
(0) = 0. 3.7 1)
а)так; б)так; 2) а)так; б)не; 3) а)так; б)не; 4) а)так; б)так.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.