2.9. 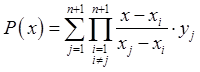 . 2.11. 1)
. 2.11. 1) ![]() і
і ![]() ,
гэта азначае, што
,
гэта азначае, што ![]() за выключэннем пунктаў
за выключэннем пунктаў ![]() і
і ![]() ;
2)
;
2) ![]() ,
, ![]() ;
3)
;
3) ![]() ;
4) калі
;
4) калі ![]() , то
, то ![]() ; калі
; калі ![]() ,
то
,
то ![]() ;
;
5) ![]() ;
6)
;
6) ![]() ; 7)
; 7) ![]() ; 8)
; 8) ![]() ; 9)
; 9) ![]() .
.
2.13. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() . 2.14. 1)
. 2.14. 1) ![]() ,
, ![]() ; 2)
; 2) ![]() ,
, ![]() . 2.15. 1)
. 2.15. 1) ![]() ; 2)
; 2) ![]() ;
;
3) ![]() . 2.16. 1)
. 2.16. 1) ![]() . Парада: скарыстайце метад
матэматычнай індук-цыі; 2)
. Парада: скарыстайце метад
матэматычнай індук-цыі; 2) ![]() ; 3)
; 3) ![]() . 2.17. Так. 2.18. 1)
. 2.17. Так. 2.18. 1) ![]() ; 2)
; 2) ![]() . 2.25. Напрыклад,
. 2.25. Напрыклад, ![]() . 2.26.
. 2.26. ![]() . 2.28.
. 2.28. ![]() .
.
2.29. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() . 2.30. Парада: будзем шукаць паслядоўнасць
у выглядзе
. 2.30. Парада: будзем шукаць паслядоўнасць
у выглядзе ![]() . З умовы
. З умовы ![]() (1) атрымліваем
(1) атрымліваем ![]() і
і ![]() .
Відавочна, што ўмову (1) задавальняе
.
Відавочна, што ўмову (1) задавальняе ![]() . Канстанты
. Канстанты ![]() і
і ![]() знаходзім
з умовы
знаходзім
з умовы ![]() .
.
2.31. Парада: 1) прыняць
ад процілеглага, што ![]() - найбольшы просты лік
і разглядзець лік
- найбольшы просты лік
і разглядзець лік ![]() ; 2) формула
агульнага элемента паслядоўнасці да гэтай пары не знойдзена.
; 2) формула
агульнага элемента паслядоўнасці да гэтай пары не знойдзена.
2.34. 1) – 5) абмежаваныя зверху і знізу; 6) абмежаваная знізу; 7)
абмежаваная зверху, калі ![]() ; абмежаваная
знізу, калі
; абмежаваная
знізу, калі ![]() . 2.35. 1), 4), 5) – не; 2), 3) – так. 2.38. Не. 2.41. Парада: скарыстаць
умову:
. 2.35. 1), 4), 5) – не; 2), 3) – так. 2.38. Не. 2.41. Парада: скарыстаць
умову: ![]() . 2.42. 1)
. 2.42. 1) ![]() ,
, ![]() ;
2)
;
2) ![]() ,
, ![]() .
2.43. Парада: разглядзець выпадкі:
.
2.43. Парада: разглядзець выпадкі: ![]() .
2.49. Не, калі
.
2.49. Не, калі ![]() . 2.50. Так. 2.51.
Не. 2.58. 1) Так; 2) не.
. 2.50. Так. 2.51.
Не. 2.58. 1) Так; 2) не.
2.59. 1) 1; 2) 1/5; 3) 16/9; 4) 0. 2.60. 1) 2/5; 2) 1/5; 3) 0; 4) 1; 5) 1; 6) 1/3; 7) b/3; 8) 1/2; 9) ![]() ;
10) –1; 11) 1; 12) 1/120. 2.62. 1)
0; 2) 0; 3) 0; 4) 2; 5) 2; 6) –1. 2.68. Парада: 1) пры
;
10) –1; 11) 1; 12) 1/120. 2.62. 1)
0; 2) 0; 3) 0; 4) 2; 5) 2; 6) –1. 2.68. Парада: 1) пры ![]() скарыстайце няроўнасць
скарыстайце няроўнасць ![]() , устанавіўшы яе з дапамогай
формулы бінома Ньютана; 2) спачатку дакажыце няроўнасць
, устанавіўшы яе з дапамогай
формулы бінома Ньютана; 2) спачатку дакажыце няроўнасць ![]() ;
;
4) спачатку
дакажыце няроўнасць ![]() . 2.69. 1)
1; 2) 1; 3) 1; 4) 3; 5)
. 2.69. 1)
1; 2) 1; 3) 1; 4) 3; 5) ![]() ; 6)
; 6) ![]() ; 7) 1; 8) 1. 2.71. 1)
0; 2) 0; 3) 0; 4) 2; парада: паколькі
; 7) 1; 8) 1. 2.71. 1)
0; 2) 0; 3) 0; 4) 2; парада: паколькі ![]() , то, замяніўшы
апошнюю лічбу 2 на 4, атрымаем:
, то, замяніўшы
апошнюю лічбу 2 на 4, атрымаем: ![]() ;
;
5) ![]() ; парада: даказаць метадам матэматычнай індукцыі, што
; парада: даказаць метадам матэматычнай індукцыі, што ![]() .
.
2.74. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() . 2.81. Парада:
дакажыце, што
. 2.81. Парада:
дакажыце, што ![]() . 2.82. Не. 2.85.
. 2.82. Не. 2.85. ![]() . 2.87. 3/2 і 1/2. 2.91. 1)
. 2.87. 3/2 і 1/2. 2.91. 1)
![]() ; 2)
; 2) ![]() .
.
2.92. 1) ![]() ; 2)
; 2) ![]() ; 3) 1, парада: скарыстаць роўнасць
; 3) 1, парада: скарыстаць роўнасць ![]() ;
4)
;
4) ![]() ; 5) 1, парада: скарыстаць роўнасць
; 5) 1, парада: скарыстаць роўнасць 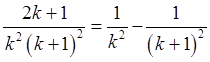 .
.
2.94. 1) 1, калі ![]() ; 0, калі
; 0, калі ![]() ; 1/2, калі
; 1/2, калі ![]() ; 2) 0, калі
; 2) 0, калі ![]() ; 1/2, калі
; 1/2, калі ![]() ; 3)
; 3) ![]() . 2.95. 1) 1/3;
парада: склаўшы розніцы
. 2.95. 1) 1/3;
парада: склаўшы розніцы ![]()
![]() , атрымаем:
, атрымаем: ![]() , адкуль знаходзім
, адкуль знаходзім ![]() . Аналагічна можна знайсці
. Аналагічна можна знайсці ![]() ; 2) 1/4; 3)
; 2) 1/4; 3) ![]() ; 4) 4/3; 5) 1/3.
; 4) 4/3; 5) 1/3.
2.98. Напрыклад, ![]() . 2.100.
. 2.100. ![]() ; парада: з формулы
; парада: з формулы 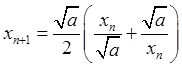 вынікае, што
вынікае, што ![]() . Адсюль і з судачынення
. Адсюль і з судачынення 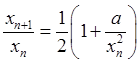 маем
маем ![]() ,
г. зн.
,
г. зн. ![]() манатонная, спадальная і
абмежаваная знізу
манатонная, спадальная і
абмежаваная знізу ![]() . Ліміт
. Ліміт ![]() вызначаецца з роўнасці
вызначаецца з роўнасці ![]() . 2.102. 1) Не
заўсёды; 2) так.
. 2.102. 1) Не
заўсёды; 2) так.
2.103. Парада: пры ![]() разгледзьце
паслядоўнасці
разгледзьце
паслядоўнасці ![]() . 2.105. 1)
1; 2) 1; 3)
. 2.105. 1)
1; 2) 1; 3) ![]() . 2.109. Парада:
скарыстайце роўнасць
. 2.109. Парада:
скарыстайце роўнасць ![]() . 2.114. 2) Не заўсёды. 2.115. 1)
. 2.114. 2) Не заўсёды. 2.115. 1) ![]() ; 2)
; 2) ![]() .
.
2.117. 1) 0; 2) ![]() ; 3) 2; 4) 0; 5) 0. 2.119. 1)
; 3) 2; 4) 0; 5) 0. 2.119. 1) ![]() ; 2) –2; 3) 1; 4) 1; 5) 10;
; 2) –2; 3) 1; 4) 1; 5) 10;
6) ![]() ; 7)
; 7)![]() .
2.120. 1) 3/2; 2) 3; 3)
.
2.120. 1) 3/2; 2) 3; 3) ![]() ;
4) –27/32; 5) 1/16;
;
4) –27/32; 5) 1/16;
6) 0, калі ![]() ;
; ![]() ,
калі
,
калі ![]() ; 7) 1; 8) 1/2. 6.121. 1)
1/4; 2) 1/4; 3) –1; 4) 3; 5) 3;
; 7) 1; 8) 1/2. 6.121. 1)
1/4; 2) 1/4; 3) –1; 4) 3; 5) 3;
6) –2; 7) ![]() ; парада: увесці новую зменную
; парада: увесці новую зменную ![]() .
.
2.123. 4) Парада: разгледзьце выпадкі ![]() і
і
![]() . 2.127.
. 2.127. ![]() . 2.128. 1) 3;
2) 0; 3)
. 2.128. 1) 3;
2) 0; 3) ![]() ;
4) 1; 5) 2/3; 6)
;
4) 1; 5) 2/3; 6) ![]() ; 7) 1/2; 8) 0; 9) 1; 10) 1; 11) 1; 12) 1;
; 7) 1/2; 8) 0; 9) 1; 10) 1; 11) 1; 12) 1;
13) 2/3. 2.129. 1) ![]() ; 2)
; 2) ![]() ; 3)
; 3) ![]() ; 4)
; 4) ![]() ; 5)
; 5) ![]() ; 6)
; 6) ![]() . 2.135. 1) непарыўная;
. 2.135. 1) непарыўная;
2) ![]() – пункт разрыву, калі
– пункт разрыву, калі ![]() ; 3)
; 3) ![]() ,
, ![]() – пункты разрыву; 4)
– пункты разрыву; 4) ![]() – пункт разрыву.
– пункт разрыву.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.