Адказы і парады. Акружына радыуса 1 з цэнтрам у пункце. Пункты разрыву першага тыпу, страница 5

3.71. Пабольшыць на 2,23 см. 3.72. a) δ_g = δ_l; б) δ_g = 2δ_T. 3.73. 1) y'' = 2; 2) y'' = 2 + 6/x⁴; 3) 1/(x² + 1)^3/2; 4) (15x³ + 36x² + 24x)/4(x + 1)^5/2;  5) (2sin3x – 6xcos3x – 9x²sin3x)/x³; 6) 2sinx/cos³x; 7) –1/x² + (ln(x + 1) + 2)/(x + 1)²ln³(x + 1); 8) –2x/(1 + x²)²;

9) (x + 1)/(–(x² + 2x))^3/2; 10) 3sinx(2cos²x – sin²x) + 2(1 – lnx)/x²; 11) 2ch2x + shx;

12) 2th³x(ch²x + 1); 13) 2 – x/(1 + x²)^3/2;  14) (5 – x)/(x – 1)³. 3.74. 44. 3.75. 36.

3.77. 1) 6dx²; 2) 2dx²; 3) –2dx²; 4) –dx²;  5) –dx²; 6) 5dx². 3.78.1) 2(3t² – 3t – 1)/(2t – 1)³;  2) –b/(a²sin³t);  3) –2cos²t/sin⁴t;  4) (t² + 2t + 2)/e^t(t + 1)³; 5) 1/3acos⁴tsint; 6) 2(1 + t)³/te^t; 7) μ(cost – μ)/a(1 – μcost)³.

3.79. 1) y'' = 2uυu'' + u²υ'' + 4uu'υ' + 2υ(u')², d²y = 2uυd²u + u²d²υ+ 4ududυ + 2υdu²;

2) y'' = (uu'' + υυ'')/+ (uυ' – υu')²/,

d²y = (ud²u + υd²υ)/+ (udυ – υdu)²/;

3) y'' = (2 + υ)u'' + 2u'υ' + uυ'', d²y = (2 + υ)d²u + 2dudυ + ud²υ; 4) y'' = ((u'' + υ'')/cos²(u + υ) + 2sin(u + υ))(u' + υ')²/cos³(u + υ),    d²y = ((d²u + d²υ)/cos²(u + υ) + 2sin(u + υ))(du + dυ)²/cos³(u + υ); 5) y'' = (uυ'' – υu'')/(u² + υ²) + (2uυ(u'² – υ'²) + 2(υ² – u²)u'υ')/(u² + υ²)²,    d²y = (ud²υ– υd²u)/(u² + υ²) + (2uυ(du² – dυ²) + 2(υ² – u²)dudυ)/(u² + υ²)²; 6) ,     .

3.80. 1) 2(1 – 8x² + 16xy + 8y + 8y²)/(1 + 2x + 2y)³; 2) 4sin(y – x)/(cos(x – y) –1)³; 3) 4(x + y)/(1 + x + y)³; 4) y/(1 – y)³; 5) 2(x² + y²)/(x – y)³. 3.81.1) 2n!; 2) (x + n)e^x; 3) y' = lnx + 1; y⁽ⁿ⁾ = (–1)ⁿ(n – 2)!/x^{n – 1}, n > 1; 4) e^x;

5) 5ⁿx(x² – 3n(n – 1)/25)cos(5x + nπ/2) + 5^{n – 1}n(3x² + (n – 1)(n –2)/25)cos(5x + (n –1)π/2)); 6) 2^{x – 1}(ln2)^{n – 1}(xln2 + n); 7) 4^{n – 2}(8x² – n(n – 1)/2)cos(4x + nπ/2) + 4^{n – 1}nxcos(4x + π(n – 1)/2), (n>2); 8) (–1)^{n – 1}(n – 1)!(1 + x²)^–n/2sin(n·arctgx); 3.82. 1) –315/8; 2) 0; 3) –1; 4) –2475·(193)!!/2⁹⁸; 5) –20!; 6) 0. 

3.83. 1) 60x²dx³; 2) 4¹⁰(x + 2,5)e^4xdx¹⁰; 3) cosxdx³/(1 + sinx)²; 4) –2·7!dx¹⁰/x⁸; 5) . 3.84. 1) 2ud³u + 6dud²u + 6dυ³ + 18υdυd²υ+ 3υ²d³υ; 2) (υ³lnυd³υ+ 3υ²du²dv – 3vdudυ² + 3υ²dud²υ– 3uvdυd²υ+ uυd³υ + 2udv³)/υ³.

3.85. 1) (x + y)(2x + 2y + 1)²dx³/(x + y – 1))⁵; 2) –3xdx³/y⁵. 3.86. 1) 2; 2) 1; 3) 3;

4) бясконца дыферэнцавальная; 5) 5. 3.87. .

3.92. 1) 0; 2)–3/8; 3)8/5; 4) 1; 5) k/n; 6) ; 7) 5; 8) 1; 9) 1/3π²; 10) 1; 11) –1; 12) 2; 13) (1–ln a); 14) a^2a(1–lna)²; 15) a²/2; 16) 3; 17) 0; 18) 1; 19) 3/2; 20) ∞; 21) 0; 22) 2;

23) –1. 3.93.1) 04 2) 1;  3) –1/6; 4) 1/3; 5) 12. 3.94.1) 0; 2). 0; 3) 0; 4) 0 пры 0<a<1; ∞, пры a>1. 3.95. 1) 1; 2) 1; 3) 1; 4) 1; 5) e; 6) 1; 7)  1/e²; 8) e^–1; 9) 1; 10) 1; 11) 1; 12) 1;

13) e⁵; 14) e^1/e; 15) e/π; 16) .  3.96. 1) 1/2; 2) 0; 3) 1; 4) 1.

3.97.1) –x²+_o(x²); 2) x²+_o(x²); 3) 1+7x/3+32x²/9 +_o(x²); 4) (1–x²/8)+_o(x²);

5) 2x+_o(x²); 6) 1-x-x²+_o(x²). 3.98.1) (x–1)+(x–1)²+_o((x–1)²);

2) sin1+2(x+1)cos1–(x+1)²(cos1+2sin1)+ +_o((x+1)²);

3) e⁴(1+(x– -4)+(x–4)²+_o((x–4)²);

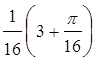4) +(x–1)–)(x––1)²+_o((x–1)²).

3.99. 1) 1++_o(x^2n–1);   2) e^–1·()+_o(x³ⁿ); 3) +_o(x²ⁿ⁺¹);  

4)  ) + _o(x^n–1);

5) 1+2x+…+nx^n–1+_o(x^n–1); 6)–x++_o(xⁿ⁺¹).

3.100. 1) e(1+)+_o(x³); 2) 1+x+x²/2+_o(x³); 3) –x–x²/2–x³/6–x⁴/12+_o(x⁴); 4) x-x²/2+_o(x³); 5) x–x²/2–x/6+x⁴/4+_o(x⁴); 6) e(1+x+x³)+_o(x³); 7) x²-x⁴/6+_o(x⁴); 8) e(1–)+_o(x³). 3.101. 1) +_o((x–1)ⁿ);

2) + +_o((x+1)^2m+1), n = 2m+1; 3) +_o((x–π/4)ⁿ); 4) e²⁺((x–1)ⁿ); 5) e³()+_o((x–1)³);

6) –2–-3+_o((x+2)ⁿ). 3.102. _o(x²ⁿ⁺²).