Федеральное агентство по образованию РФ
Государственное образовательное учреждение высшего профессионального образования
Северо - Западный государственный заочный технический университет
Институт приборостроения и систем обеспечения безопасности
Кафедра метрологии
6 курс
шифр: 4510303848
форма обучения: заочная
Специальность: 200501
Проверил:
Санкт-Петербург
2008г.
Работа №1
Проверка справедливости и экспериментальное исследование основного постулата метрологии.
Цель работы – экспериментальная проверка и усвоение основного постулата метрологии.
Группе людей было предложено измерить на глаз рост выбранного человека. Все экспериментальные данные были собраны в единый массив данный, в метрах:
Хi = 1,81 ; 1,83 ; 1,77 ; 1,89 ; 1,81 ; 1,82 ; 1,78 ; 1,74 ; 1,70 ;
1,82 ; 1,82; 1,87 ; 1,77 ; 1,83 ; 1,74 ; 1,86 ; 1,83 ; 1,78 .
Внесу поправку на
высоту каблука, равную ![]() .
.
Получу независимые значения результата измерения , определённые по формуле:
![]() = 1,79
; 1,81 ; 1,75 ; 1,87 ; 1,79 ; 1,80 ; 1,76 ; 1,72 ; 1,68 ;
= 1,79
; 1,81 ; 1,75 ; 1,87 ; 1,79 ; 1,80 ; 1,76 ; 1,72 ; 1,68 ;
1,80 ; 1,80 ; 1,85 ; 1,75 ; 1,81 ; 1,72 ; 1,84 ; 1,81 ; 1,76 .
Данный массив данных представлю в виде таблицы 1.
Таблица 1
|
Интервал измеренных значений, м |
Число значений в интервале |
|
1,66 … 1,70 |
1 |
|
1,70 … 1,74 |
2 |
|
1,74 … 1,78 |
4 |
|
1,78 … 1,82 |
8 |
|
1,82 … 1,86 |
2 |
|
1,86 … 1,90 |
1 |
На основании экспериментальных данных построю гистограмму (рис.1), используя правила построения гистограмм.
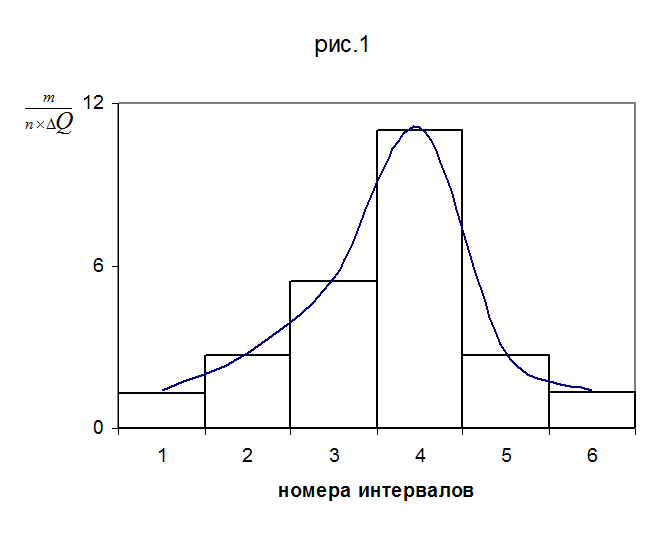
По виду представленной диаграммы можно выдвинуть гипотезу о том, что результат измерения подчиняется нормальному закону распределения вероятности. Поскольку n = 18, для проверки гипотезы о нормальности закона распределения вероятности результата измерения используется составной критерий. В этом случае необходимо рассчитать:
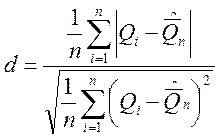 |
Результаты вспомогательных вычислений сведены в табл. 2
Таблица 2
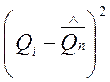 |
|||
|
, м |
, м |
, |
||||||
|
1 |
2 |
3 |
||||||
|
1,79 |
0,01 |
0,0001 |
||||||
|
1,81 |
0,03 |
0,0009 |
||||||
|
1,75 |
-0,03 |
0,0009 |
||||||
|
1,87 |
0,09 |
0,0081 |
||||||
|
1,79 |
0,01 |
0,0001 |
||||||
|
1,80 |
0,02 |
0,0004 |
||||||
|
1,76 |
-0,02 |
0,0004 |
||||||
|
1,72 |
-0,06 |
0,0036 |
||||||
|
1,68 |
-0,10 |
0,01 |
||||||
|
1,80 |
0,02 |
0,0004 |
||||||
|
1,80 |
0,02 |
0,0004 |
||||||
|
1,85 |
0,07 |
0,0049 |
||||||
|
1,75 |
-0,03 |
0,0009 |
||||||
|
1,81 |
0,03 |
0,0009 |
||||||
|
1,72 |
-0,06 |
0,0036 |
||||||
|
1,84 |
0,06 |
0,0036 |
||||||
|
1,81 |
0,03 |
0,0009 |
||||||
|
1,76 |
-0,02 |
0,0004 |
||||||
|
|
|
|
На основании выполненных расчётов d = 0,822 .
![]()
![]() Согласно табл.11 (Шишкин И.Ф. Теоретическая
метрология) условие
Согласно табл.11 (Шишкин И.Ф. Теоретическая
метрология) условие
соблюдается с вероятностью . .
![]()
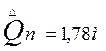 При n =18 не более одного результата измерения Qi c
вероятностью 0,98 может отличаться от среднего арифметического значения больше
, чем на .
При n =18 не более одного результата измерения Qi c
вероятностью 0,98 может отличаться от среднего арифметического значения больше
, чем на .
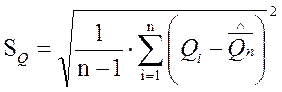 Так как
Так как
= 0,05 м ,
![]() то из второго столбца таблицы следует, что ни один результат измерения Qi не
отличается от больше, чем на
то из второго столбца таблицы следует, что ни один результат измерения Qi не
отличается от больше, чем на ![]() .
.
Следовательно, гипотеза о нормальности закона распределения вероятности результата измерения может быть принята с вероятностью
Р = 0,99+0,98-1=0,97
Выражение для плотности распределения вероятности результата измерения, подчиняющегося нормальному закону, имеет вид:
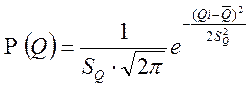 ,
,
при 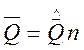 получим
получим 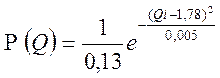 ,
,
Результаты расчёта Р(Q) сведены в табл. 3.
Таблица 3
|
№ пп |
|
|
|
P(Q) |
|
1 |
1,68 |
0,0108 |
2,16 |
0,009 |
|
2 |
1,75 |
0,00125 |
0,25 |
0,06 |
|
3 |
1,78 |
0,000016 |
0,003 |
0,08 |
|
4 |
1,84 |
0,00314 |
0,63 |
0,04 |
|
5 |
1,87 |
0,0074 |
1,48 |
0,02 |
По данным таблицы построю график плотности распределения вероятности результата измерения. Результат наложения его на гистограмму показан на рис. 2
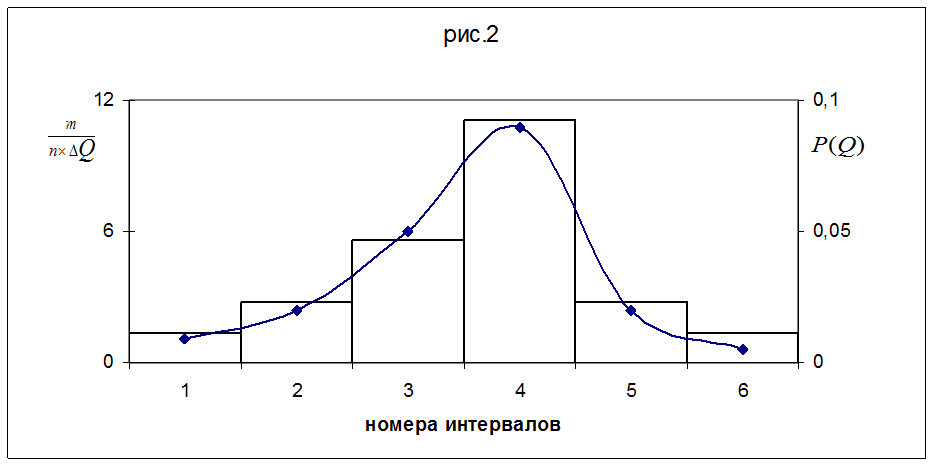 |
1.2 Измерение периметра помещения с помощью измерительной линейки.
Получен следующий массив экспериментальных данных, в метрах :
Хi = 18,344 ; 18,223 ; 18,159 ; 18,276 ; 18,29 ; 18,266;
18,231 ; 18,278 ; 18,283 ; 18,111 ; 18,339 ; 18,285;
18,373 ; 18,168 ; 18,261 ; 18,198 ; 18,222 ; 18,245.
Данный массив данных представлю в виде таблицы 1.2.1 :
Таблица 1.2.1
|
Интервал измеренных значений, м |
Число значений в интервале |
|
18,10… 18,15 |
1 |
|
18,15…18,20 |
3 |
|
18,20…18,25 |
4 |
|
18,25…18,30 |
7 |
|
18,30…18,35 |
2 |
|
18,35…18,40 |
1 |
Полагая поправку равной нулю, будем считать, что Qi = Xi .
На основании экспериментальных данных построю гистограмму (рис.1.2.1), используя правила построения гистограмм.
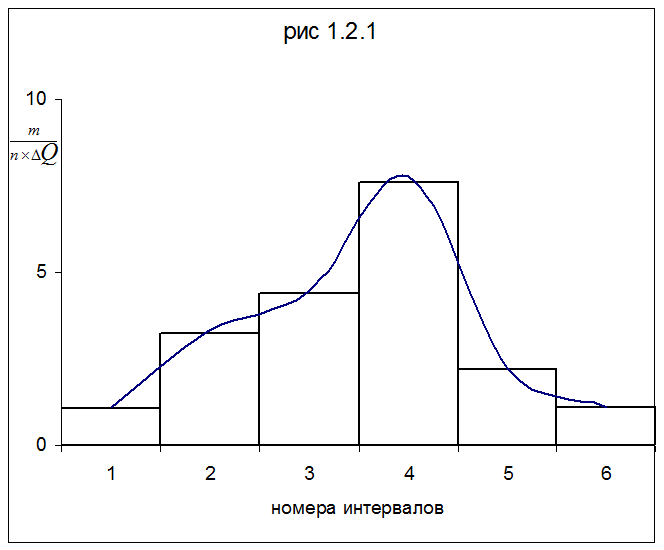
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.