Проверка справедливости и экспериментальное исследование основного постулата метрологии, страница 2

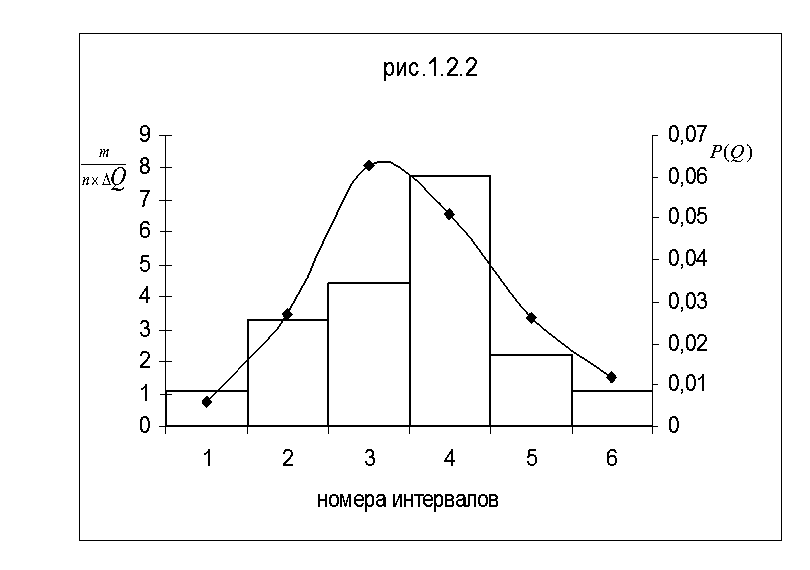
По виду представленной диаграммы можно выдвинуть гипотезу о том, что результат измерения подчиняется нормальному закону распределения вероятности. Поскольку n = 18, для проверки гипотезы о нормальности закона распределения вероятности результата измерения используется составной критерий. В этом случае необходимо рассчитать:

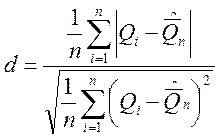Результаты вспомогательных вычислений сведены в табл.1.2.2                                                                              

                                                                                         Таблица 1.2.2

,  м	,             , м	,
1	2	3
18,344	0,091	0,008281
18,223	-0,03	0,000900
18,159	-0,094	0,008836
18,276	0,023	0,000529
18,290	0,037	0,001369
18,266	0,013	0,000169
18,231	-0,022	0,000484
18,278	0,025	0,000625
18,283	0,03	0,000900
18,111	-0,142	0,020164
18,339	0,086	0,007396
18,285	0,032	0,001024
18,373	0,12	0,014400
18,168	-0,085	0,007225
18,261	0,008	0,000064
18,198	-0,055	0,003025
18,222	-0,031	0,000961
18,245	-0,008	0,000064

    На основании выполненных расчётов d = 0,8 .

    Согласно табл.11 (Шишкин И.Ф. Теоретическая метрология) условие       

 соблюдается с вероятностью                .   .

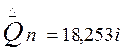
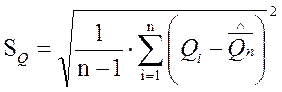   При n =18 не более одного результата измерения Qi  c вероятностью 0,98 может отличаться от среднего арифметического значения                        больше , чем на                     .

Так как

                                                           = 0,067 м ,

то из второго столбца таблицы следует, что ни один результат измерения Qi не отличается от          больше, чем на  .

     Следовательно, гипотеза о нормальности закона распределения вероятности результата измерения может быть принята с вероятностью

Р = 0,99+0,98-1=0,97

     Выражение для плотности распределения вероятности результата измерения, подчиняющегося нормальному закону, имеет вид:

,

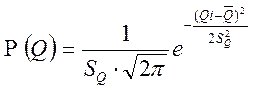при 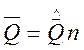 получим              ,

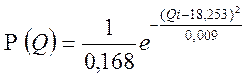        Результаты расчёта Р(Q) сведены в табл.1.2.3.

                                                                                                       Таблица 1.2.3

№ пп	, м	,		P(Q)
1	18,111	0,020164	2,24	0,006
2	18,168	0,007225	0,803	0,027
3	18,231	0,000484	0,054	0,063
4	18,290	0,001369	0,152	0,051
5	18,339	0,007396	0,822	0,026
6	18,373	0,014400	1,6	0,012

    По данным таблицы построю график плотности распределения вероятности результата измерения. Результат наложения его на гистограмму показан на рис.1.2.2

 

Отчёт по работе  №2

Многократное измерение.

    Цель работы – приобретение навыков выполнения и обработки многократных измерений.

2.1  Измерение (на ощупь) температуры оконного стекла. 

Три группы людей проводили измерения на (на ощупь) температуры оконного стекла. Получены следующие три массива экспериментальных данных, в  :

                          =  12 ; 13 ; 12 ; 9 ; 11; 12 ; 10.        

                          =   12 ; 13 ; 12 ; 9 ; 11 ; 12 ; 10 ;

                        14 ; 10 ; 13 ; 11; 12; 13 ; 13.

                          =   13 ; 11 ; 12 ; 13 ; 16 ;  9 ;  8   ; 10  ;   9 ; 11 ; 12 ; 13 ;  9 ;  11; 10;

                                       14 ; 10 ;  13 ; 15 ; 14 ; 10 ; 9   ; 11 ; 12  ; 13 ;  8 ; 15 ; 11 ; 10 ; 7  ;

                                        9  ; 12 ;  10 ; 11 ;  8  ; 12 ; 14 ; 10 ;  10 ; 10 ; 11;  9  ; 15 ; 12 ; 13;

     Полагая поправку равной нулю, будем считать, что Qi = Xi .

     Вычислю среднее арифметическое значение и стандартное отклонение результата измерения для каждого из трёх массивов экспериментальных  данных  1…3. Результаты расчёта сведены в таблицу 2.1

                                                                                           Таблица 2.1

Массив	,	,	,
1	11,3	1,38	4,14
2	11,8	1,42	4,27
3	11,2	2,15	6,46

      Проверка по правилу «трёх сигм» показала, что массивах 1…3  не содержится ошибок.

      Анализ условий проведения измерительного эксперимента показывает, что факторы, оказывающие доминирующее влияние на рассеяние результата измерения, отсутствуют. Можно предположить, что он подчиняется нормальному закону распределения вероятности для массивов экспериментальных данных 2 и 3.

      Проверю гипотезу о соответствии экспериментальных данных нормальному закону распределения вероятности результатов измерения  с помощью критерия Пирсона. При этом в каждом интервале должно быть не менее пяти независимых значений результата измерения. Результаты расчётов сведены в табл.2.2

Таблица 2.2

i	Интервал
1		10	-0,977	-0,3365	0,1635	2,64	0,947
2		16	0,04	0,0160	0,3525	0,14	0,001
3		12	1,07	0,3577	0,3417	-3,38	0,743
4		7		0,5	0,1423	0,6	0,056