Проверка справедливости и экспериментальное исследование основного постулата метрологии, страница 4

2. Выполнено однократное измерениетемпературы  оконного стекла: .

3. Получу результат однократного измерения :  .

4. Установлю пределы, в которых с вероятностью 0,95 находится измеренное значение  температуры  оконного стекла Обозначив половину доверительного интервала через  , найду, что с вероятностью 0,95:

Q = 8,2 … 13,8  .

5. При сравнении результата однократного и многократного измерения подтвердилось, что среднее квадратическое отклонение результата многократного измерения  в  раз меньше средне квадратического отклонения результата однократного измерения   :

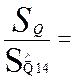
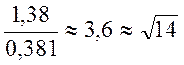
    Вывод: необходимым условием проведения однократного измерения служит наличие априорной информации. Доверительная вероятность является мерой достоверности измерений.

Отчёт по работе  №4

Обеспечение требуемой точности измерений.

      Цель работы – практическое освоение процедуры обеспечения требуемой точности результата измерения физической величиныпостоянного размера.

4.1 Визуальное измерение роста человека

   Используя материалы работы 1.1, определю, при каком количестве отсчётов n рост человека может быть измерен со стандартным отклонением   () :

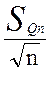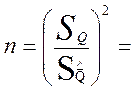
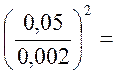т.к.   =      , то      625

     По графику вероятности попадания среднего арифметического в окрестность среднего значения вычислю t (коэффициент Стьюдента) при доверительной вероятности :

t = 2,85  ;   м

   Запишу с установленной точностью результат многократного измерения в форме оценок числовых характеристик его закона распределения вероятности :

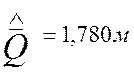   ;     при   n=625

Q = 1,774… 1,786 м

4.2   Измерение на ощупь температуры  оконного стекла.

   Используя материалы работы 1.3, определю, при каком количестве отсчётов n температура  оконного стекла может быть измерена со стандартным отклонением   () :

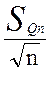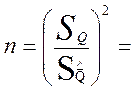
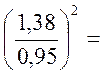т.к.   =      , то      2

     По графику вероятности попадания среднего арифметического в окрестность среднего значения вычислю t (коэффициент Стьюдента) при доверительной вероятности :

t = 2,85  ;  

   Запишу с установленной точностью результат многократного измерения в форме оценок числовых характеристик его закона распределения вероятности :

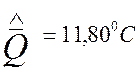   ;     при   n=2

Q = 9,09 … 14,51

4.3   Измерение периметра помещения  с помощью измерительной линейки.

      Используя материалы работы 1.2, определю, при каком количестве отсчётов n периметр помещения  может быть измерен со стандартным отклонением   () :

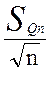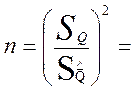
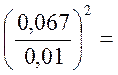т.к.   =      , то      45

     По графику вероятности попадания среднего арифметического в окрестность среднего значения вычислю t (коэффициент Стьюдента) при доверительной вероятности :

t = 2,85  ;  

   Запишу с установленной точностью результат многократного измерения в форме оценок числовых характеристик его закона распределения вероятности :

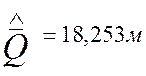   ;     при   n=45

Q = 18,224 … 18,282 м

4.4    Измерение рукой массы предмета.

      Используя материалы работы 1.2, определю, при каком количестве отсчётов n периметр помещения  может быть измерен со стандартным отклонением   () :

т.к.   = 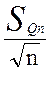     , то 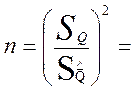 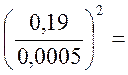    144400

     По графику вероятности попадания среднего арифметического в окрестность среднего значения вычислю t (коэффициент Стьюдента) при доверительной вероятности :

t = 2,85  ;  

   Запишу с установленной точностью результат многократного измерения в форме оценок числовых характеристик его закона распределения вероятности :

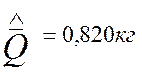   ;     при   n=144400

Q = 0,819 … 0,821 кг

  Вывод : многократное измерение одной и той же величины постоянного размера позволяет обеспечить требуемую точность. Однако точность многократного измерения ограничивается дефицитом информации.

Отчёт по работе  №5

Обработка экспериментальных данных, полученных в нескольких сериях измерений.

      Цель работы – приобретение практических навыков обработки экспериментальных данных, полученных в нескольких сериях измерений.

1. Используя результаты работы 2.2, сравню между собой средние арифметические двух серий измерений температуры оконного стекла. Получены следующие два массива экспериментальных данных, в :

                                =   0,4   ; 0,55 ; 0,75 ; 0,9 ; 0,8 ; 0,5 ;  1,0;

                             0,95 ;  0,9  ; 1,2 ; 1,0 ; 0,95 ; 0,8 ; 0,85

                                =  13 ; 11 ; 12 ; 13 ; 16 ;  9 ;  8   ; 10  ;   9 ; 11 ; 12 ; 13 ;  9 ;  11; 10;

                                            14 ; 10 ;  13 ; 15 ; 14 ; 10 ; 9   ; 11 ; 12  ; 13 ;  8 ; 15 ; 11 ; 10 ; 7  ;

                                            9  ; 12 ;  10 ; 11 ;  8  ; 12 ; 14 ; 10 ;  10 ; 10 ; 11;  9  ; 15 ; 12 ; 13;

2. Определю значимость различия между средними арифметическими в двух сериях :

    ;        ;   

                                      ;       ;    

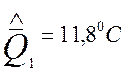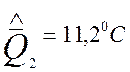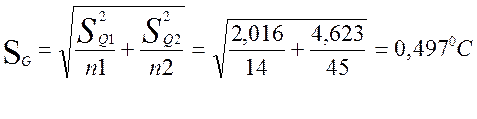
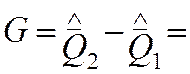11,2 – 11,8 = -0,6

   При доверительной вероятности   и t = 1,9 найду доверительные границы  . Проверю, выполняется ли равенство :  ;   ;  .  Неравенство выполняется, следовательно, различие между средними арифметическими в сериях считается незначимым.

3.   Проверю значимость различий оценок дисперсий в двух сериях в соответствии с алгоритмом. В процессе вычислений образуется отношение 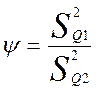 , вероятность значений которого, больших единицы, если это число случайное, подчиняется распределению Р.А.Фишера.

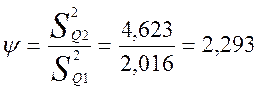
    Выберу значение интегральной функции распределения вероятности Р.А.Фишера с вероятностью  . =2,4.

    серии равнорассеянны.

 4.  Т.к.  различие между средними арифметическими в сериях считается незначимым и серии равнорассеянны, данные серии можно считать однородными. Выполню обработку экспериментальных данных, входящих в серии. Экспериментальные данные при этом обрабатываются как единый массив.

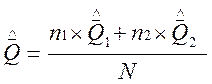   ,    N = n1 + n2

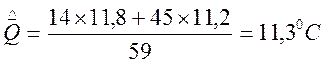
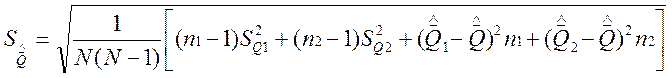
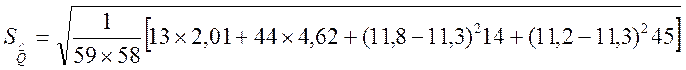= 0,26

С вероятностью    определю по графику коэффициент Стьюдента t . t = 1,9.

Q = 10,8 … 11,8 

   Вывод : проверка однородности является обязательной при выборке способа совместной обработки результатов нескольких серий измерений. Экспериментальные данные, входящие в данные серии, можно обрабатывать как единый массив.

Литература

    1. Шишкин И.Ф. Теоретическая метрология. – М.: Высшая школа, 1993

    2. Практикум по метрологии. Основы измерений. Методические указания к практическим занятиям. Санкт-Петербург, 2004г.