Проверка справедливости и экспериментальное исследование основного постулата метрологии, страница 3

     Суммирование чисел в восьмой графе табл.2.2 даёт    . Из графика интегральной функции распределения вероятности К.Пирсона видно, что рассчитанное значение для вероятности 0,95. Таким образом, с вероятностью 0,95 можно принять гипотезу о том, что результат измерения подчиняется нормальному закону.

     Стандартное отклонение среднего арифметического в каждом из трёх массивов экспериментальных данных:

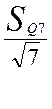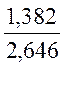              =    =  = 0,522   ;   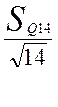   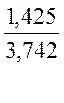  =  =  = 0,381   ;

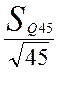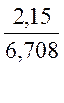     =  =  = 0,321

Результаты многократного измерения температуры оконного стекла, полученные каждой из групп:

 ; ;  ; ; ;

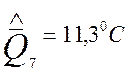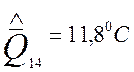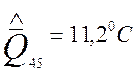    Пределы, в которых находится значение температуры оконного стекла, устанавливаются по формуле:

  ,

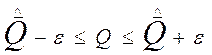     где    , а коэффициент Стьюдента t зависит от доверительной вероятности P. При Р= 0,95, используя график вероятности попадания среднего арифметического в окрестность среднего значения, получаю , , . С вероятностью 0,95 имеем:

Q = 10,0 … 12,6     при  n=7;

Q = 11,0… 12,6     при  n=14;

Q = 10,6 … 11,8    при n=45.

2.2  Измерение рукой массы предмета

Три группы людей проводили измерения рукой массы предмета. Получены следующие три массива экспериментальных данных, в кг:

     =  0,8 ;  0,85 ; 0,7 ; 0,4 ; 0,55 ; 0,75 ; 0,9 ;

   =  0,4   ; 0,55 ; 0,75 ; 0,9 ; 0,8 ; 0,5 ;  1,0;

               0,95 ;  0,9  ; 1,2 ; 1,0 ; 0,95 ; 0,8 ; 0,85 .                                                                     

  =   0,75 ; 0,9  ;  0,8 ;  0,75 ; 0,5 ; 1,0 ; 0,95 ;  0,9  ; 0,65; 1,0 ; 0,95 ; 0,8 ; 0,85 ; 0,45 ; 1,25;

                0,8  ; 0,95 ;  1,1 ;  1,1 ; 1,0 ; 0,9  ; 0,85 ;  1,0 ;  0,9 ; 1,0 ; 0,95 ; 1,2 ;  1,3  ;  1,1 ; 0,9;

           0,55 ; 1,0  ;  0,95 ; 1,1 ; 0,8 ; 0,65 ; 0,8 ; 0,85 ; 0,95 ; 1,1 ; 1,15 ; 1,2 ; 0,9 ; 0,9 ; 0,85.

     Полагая поправку равной нулю, будем считать, что Qi = Xi .

     Вычислю среднее арифметическое значение и стандартное отклонение результата измерения для каждого из трёх массивов экспериментальных  данных  1…3. Результаты расчёта сведены в таблицу 2.2.1

                                                                                                              Таблица 2.2.1

Массив	, кг	, кг	,  кг
1	0,71	0,17	0,51
2	0,83	0,22	0,66
3	0,93	0,18	0,55

      Проверка по правилу «трёх сигм» показала, что массивах 1…3  не содержится ошибок.

      Анализ условий проведения измерительного эксперимента показывает, что факторы, оказывающие доминирующее влияние на рассеяние результата измерения, отсутствуют. Можно предположить, что он подчиняется нормальному закону распределения вероятности для массивов экспериментальных данных 2 и 3.

      Проверю гипотезу о соответствии экспериментальных данных  третьего массива нормальному закону распределения вероятности результатов измерения  с помощью критерия Пирсона. При этом в каждом интервале должно быть не менее пяти независимых значений результата измерения. Результаты расчётов сведены в табл.2.2.2

Таблица 2.2.2

i	Интервал
1		5	-1,444	-0,4251	0,0749	1,63	0,788
2		11	-0,167	-0,0675	0,3576	-5,09	1,61
3		24	1,111	0,3665	0,434	4,47	1,023
4		5		0,5	0,1335	-1,01	0,17

     Суммирование чисел в восьмой графе табл.2.2.2  даёт    . Из графика интегральной функции распределения вероятности К.Пирсона видно, что рассчитанное значение   для вероятности 0,95. Таким образом, с вероятностью 0,95 можно принять гипотезу о том, что результат измерения подчиняется нормальному закону.

     Стандартное отклонение среднего арифметического в каждом из трёх массивов экспериментальных данных:

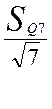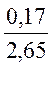                     =    =  = 0,06 кг    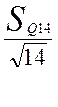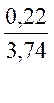;        =  =  = 0,06 кг   ;

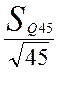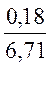     =  =  = 0,03 кг

Результаты многократного измерения температуры оконного стекла, полученные каждой из групп:

 ; ;  ; ; ;

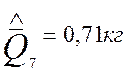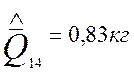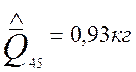    Пределы, в которых находится значение температуры оконного стекла, устанавливаются по формуле:

  ,

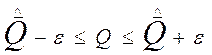где    , а коэффициент Стьюдента t зависит от доверительной вероятности P. При Р= 0,95, используя график вероятности попадания среднего арифметического в окрестность среднего значения, получаю , , . С вероятностью 0,95 имеем:

Q = 0,56  … 0,86 кг    при  n=7;

 Q = 0,70 … 0,96 кг    при  n=14;

Q = 0,87  … 0,99 кг   при n=45.

    Вывод:  точность определения значения измеряемой величины повышается при увеличении числа измерений. Используя массив экспериментальных данных, можно определить числовые характеристики закона распределения вероятности результата измерения, указав пределы, в которых они находятся с определённой вероятностью.

Отчёт по работе  №3

Однократное измерение.

  Цель работы – приобретение навыков выполнения и обработки однократных измерений.

3.1 Однократное измерение (на глаз) роста человека.

1.  Априорная информация: нормальный закон распределения вероятности ; стандартное отклонение   ; значение поправки .

2. Выполнено однократное измерение роста человека :

3. Внесу поправку и получу результат однократного измерения по формуле :  ;

    Ширина интервала, в котором устанавливается значение измеряемой величины, зависит от выбранной доверительной вероятности. Задавшись вероятностью 0, 95 , по верхней кривой вероятности попадания отдельного значения результата измерения в окрестность среднего значения  (Шишкин И.Ф. Теоретическая метрология , рис.22) определю, на сколько  результат однократного измерения  может отличаться от среднего значения результата измерения  , равного значению измеряемой величины Q. Обозначив половину доверительного интервала через  , найдём, что с вероятностью 0,95:

Q = 1,70…1,90 м

4. При сравнении результата однократного и многократного измерения подтвердилось, что среднее квадратическое отклонение результата многократного измерения  в  раз меньше средне квадратического отклонения результата однократного измерения   :

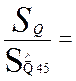
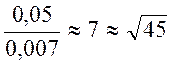
3.2  Однократное измерение на ощупь температуры  оконного стекла.                     

1. Априорная информация: нормальный закон распределения вероятности ; стандартное отклонение   ; значение поправки .